请选择
返回
很多同学都想知道圆的内接四边形具有哪些性质,大家一起来看看吧。

圆的内接四边形性质
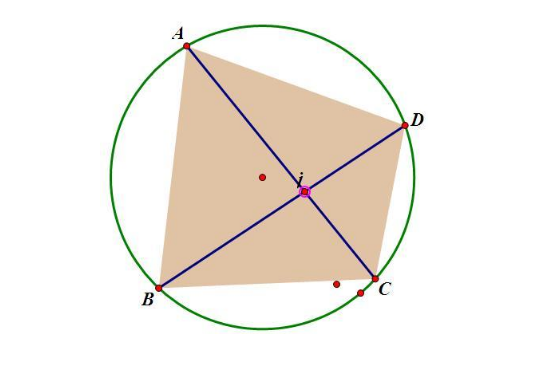
以圆内接四边形ABCD为例,圆心为O,延长AB至E,AC、BD交于P,则:
1、圆内接四边形的对角互补:∠BAD+∠DCB=180°,∠ABC+∠ADC=180°
2、圆内接四边形的任意一个外角等于它的内对角:∠CBE=∠ADC
3、圆心角的度数等于所对弧的圆周角的度数的两倍:∠AOB=2∠ACB=2∠ADB
4、同弧所对的圆周角相等:∠ABD=∠ACD
5、圆内接四边形对应三角形相似:△ABP∽△DCP(三个内角对应相等)
6、相交弦定理:AP×CP=BP×DP
7、托勒密定理:AB×CD+AD×CB=AC×BD
圆的内接四边形判定定理
1、如果一个四边形的对角互补,那么这个四边形内接于一个圆;
2、如果一个四边形的外角等于它的内对角,那么这个四边形内接于一个圆;
3、如果一个四边形的四个顶点与某定点等距离,那么这个四边形内接于以该点为圆心的一个圆;
4、若有两个同底的三角形,另一顶点都在底的同旁,且顶角相等,那么这两个三角形有公共的外接圆;
5、如果一个四边形的张角相等,那么这个四边形内接于一个圆;
6、相交弦定理的逆定理;
7、托勒密定理的逆定理。
内切圆与外切圆
1、关于内切圆和外切圆。只有两圆相切时,才有内切圆和外切圆之说。当然,里面是内切圆。外面的为外切圆。即,当且仅当圆内有圆或椭圆时,才有外切圆概念。
2、内切圆。圆在几何图形内(可以是圆),圆周与外侧几何图形的边(或圆周)相切。
3、内接圆不存在。内接图形只能是圆以外的几何图形。由内接三角形、正方形等。
4、外接圆,几何图形在圆内,而其向顶点在此圆周上。
以上就是一些圆的内接四边形的相关信息,供大家参考。