请选择
返回
验证两个全等三角形一般用边边边(SSS)、边角边(SAS)、角边角(ASA)、角角边(AAS)、和直角三角形的斜边,直角边(HL)来判定。
判定方法
1、SSS:即三边对应相等的两个三角形全等。
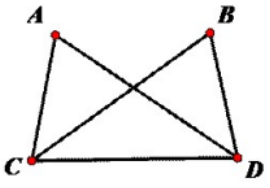
如下图,AC=BD,AD=BC,求证∠A=∠B。
证明:在△ACD与△BDC中{AC=BD,AD=BC,CD=CD。∴△ACD≌△BDC。∴∠A=∠B。
2、SAS:即三角形的其中两条边对应相等,且两条边的夹角也对应相等的两个三角形全等。
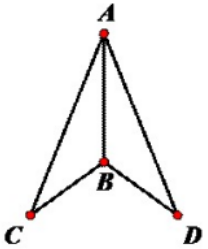
如下图,AB平分∠CAD,AC=AD,求证∠C=∠D。
证明:∵AB平分∠CAD。∴∠CAB=∠BAD。在△ACB与△ADB中{AC=AD,∠CAB=∠BAD,AB=AB。∴△ACB≌△ADB。∴∠C=∠D。
3、AAS:即三角形的其中两个角对应相等,且对应相等的角所对应的边也对应相等的两个三角形全等。
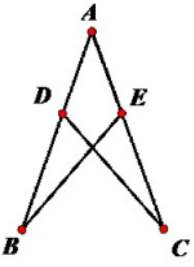
如下图,AB=DE,∠A=∠E,求证∠B=∠D。
证明:在△ABC与△EDC中{∠A=∠E,∠ACB=∠DCE,AB=DE。∴△ABC≌△EDC。∴∠B=∠D。

4、ASA:即三角形的其中两个角对应相等,且两个角夹边也对应相等的两个三角形全等。
如下图,AB=AC,∠B=∠C,求证△ABE≌△ACD。
证明:在△ABE与△ACD中{∠A=∠A,AB=AC,∠B=∠C。∴△ABE≌△ACD。
全等三角形的性质
(1)全等三角形的对应角相等。
(2)全等三角形的对应边相等。
(3)能够完全重合的顶点叫对应顶点。
(4)全等三角形的对应边上的高对应相等。
(5)全等三角形的对应角的角平分线相等。
(6)全等三角形的对应边上的中线相等。
(7)全等三角形面积和周长相等。
(8)全等三角形的对应角的三角函数值相等。