请选择
全等三角形的五种证明方法有边边边:三边对应相等的两个三角形全等;边角边:两边和它们夹角对应相等的两个三角形全等;角边角公理(ASA):两角和它们的夹角对应相等的两个三角形全等;角角边:两个角和其中一角的对边对应相等的两个三角形全等;斜边直角边定理:斜边和一条直角边对应相等的两个直角三角形全等。

方法一:边边边(SSS)
三条边都对应相等的两个三角形全等
三角形具有稳定性,三条边都确定了,整个三角形都可以固定下来了。这样就具有了唯一性,而这样的两个三边都对应相等的三角形,自然就是全等的。但是需要注意的是三个角都相等的两个三角形不能判定全等。
边边证明的例题
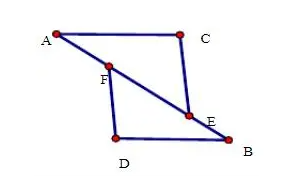
已知如下:A、B、E、F在同一条直线上,且AC=BD,CE=DF,AF=BE。
求证:ACE ≌ BDF
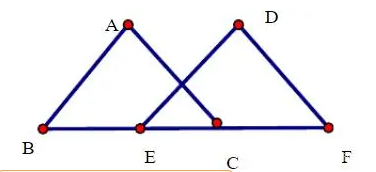
已知如下:B、E、C、F在同一条直线上,且AB=DE,AC=DF,BE=CF。
求证:ABC ≌ DEF
这两个例题都是通过方法一:边边边来证明两个三角形全等的。其中两条对应的边相等是题目已经给出的,还有一个条件给出一部分边相等,但是它们存在相互重合的部分,也就是公共边。既然重合,自然相等,两段相等的边相加,第三条边相等的条件也就出来了。
方法二:边角边(SAS)
两边和它们之间的夹角对应相等的两个三角形全等
这个判定方式是课本上直接给出的:同一个角度的有很多,但是确定了夹这个角的两条边的长短,这个就被确定下来了。
边角边证明的例题
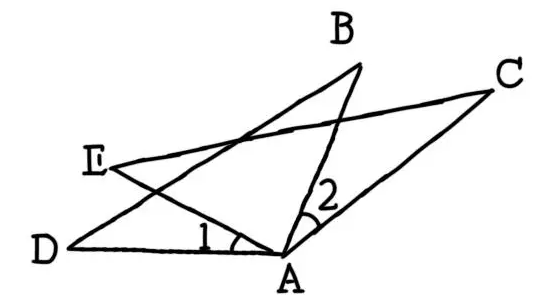
已知如下:AB=AC,AD=AE,∠1=∠2。
求证:ABD ≌ ACE
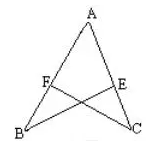
已知如下:AB=AC,且E、F分别是AC、AB的中点。
求证:ABD ≌ ACE
这两个例题都是通过方法二:边角边来证明三角形全等的。其中2-1题需要知道那两个夹角中存在公共角,公共角相等,题目又提到∠1=∠2,因此夹角相等。而2-2题可以明显看出两个三角形共用一个夹角,所以要推出两边对应相等,AB=AC再加上中点,很容易就可以证明出来了。
方法三:角边角(ASA)
两角和它们之间的夹边对应相等的两个三角形全等
这个判定方式也是课本上直接给出的:一个角的边可以无限延长,两个角的夹边被确定以后,就无法延长了,另外两条边则肯定会有交点,这样肯定也能将三角形确定下来。
角边角证明例题
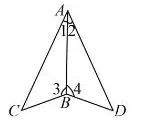
已知如下:∠1=∠2,∠3=∠4。
求证:ABC ≌ ABD
已知如下:∠CAB=∠DBA,∠ABC=∠BAD。
求证:BC=AD
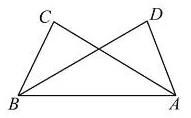
以上两个例题就是利用方法三:角边角证明三角形全等的。题目中都给出了两个角对应相等的条件,而夹边是共用的,所以也是相等的,证明全等也是很容易的。值得注意的是3-2中,它让你证明的是两条边相等,其实这是让你先证明三角形全等之后,由全等来证明两条对应的边相等。