请选择
返回
梯形中位线定理是指连接梯形两腰中点的线段。梯形的中位线平行于两底,并且等于两底和的一半。接下来分享梯形中位线定理的证明方法,供参考。

梯形中位线定理证明方法
如图,四边形ABCD是梯形,AD∥BC,E、F分别是AB、CD边上的中点,求证:EF∥AD,且EF=(AD+BC)/2
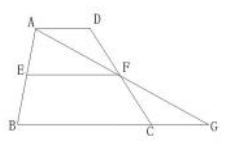
证明:
连接AF并延长交BC的延长线于G。
∵AD∥BC
∴∠ADF=∠GCF
∵F是CD的中点
∴DF=FC
∵∠AFD=∠CFG
∴△ADF≌△GCF(ASA)
∴AF=FG,AD=CG
∴F是AG的中点
∵E是AB的中点
∴EF是△ABG的中位线
∴EF∥BG,EF=BG/2=(BC+CG)/2
∴EF=(AD+BC)/2
∵AD∥BC
∴EF∥AD∥BC
梯形中位线定理
连接梯形两腰中点的线段叫做梯形的中位线,梯形的中位线平行于两底,并且等于两底和的一半。
梯形的中位线L平行于底边,且其长度为上底加下底和的一半,用符号表示是:L=(a+b)/2。
中位线在关于梯形的各种题型中都是一条得天独厚的辅助线。
梯形的计算公式
1、梯形的周长公式:上底+下底+腰+腰,用字母表示:L=a+b+c+d。
2、等腰梯形的周长公式:上底+下底+2腰,用字母表示:a+c+2b。
3、梯形的面积公式:(上底+下底)×高÷2,用字母表示:S=(a+c)×h÷2。
4、对角线互相垂直的梯形面积为:对角线×对角线÷2。