请选择
返回
三角形外角平分线定理是三角形外角的平分线如果和对边的延长线相交,它按照夹相应角的两边的比外分对边。接下来分享证明方法,供参考。

外角平分线定理证明方法
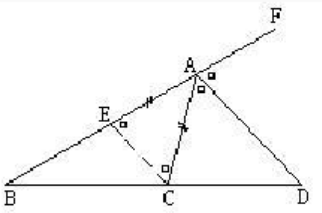
如图,AD是△ABC中∠BAC的外角∠CAF的平分线。求证:BA/AC=BD/DC
证明:过C作CE∥DA与BA交于E。则:BA/AE=BD/DC
∵∠DAF=∠CEA;∠DAC=∠ECA;∠DAF=∠DAC。
∴∠CEA=∠ECA;∴AE=AC;∴BA/AC=BD/DC。
内角平分线定理证明方法
角平分线线上的点到角两边的距离相等。
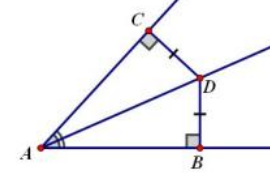
若射线AD是∠CAB的角平分线,求证:CD=BD
∵∠DCA=∠DBA
∠CAD=∠BAD
AD=AD
∴△ACD≌△ABD
∴CD=BD
角平分线的性质定理
1.角平分线可以得到两个相等的角。
2.角平分线上的点到角两边的距离相等。
3.三角形的三条角平分线交于一点,称作三角形内心。三角形的内心到三角形三边的距离相等。
4.三角形一个角的平分线,这个角平分线其对边所成的两条线段与这个角的两邻边对应成比例。