2018年长治市中考数学模拟试题（word版，含答案）

各位同学在查看时请点击全屏查看

2018年长治市中考数学模拟试题

注意事项：

1.本试卷分第Ⅰ卷和第Ⅱ卷两部分.全卷共6页，满分120分，考试时间120分钟.

2.答卷前，考生务必将自己的姓名、准考证号填写在本试卷相应的位置.

3.答案全部在答题卡上完成，答在本试卷上无效.

4.考试结束后，将本试卷和答题卡一并交回.

一、数学模拟试题选择题（本大题共 10个小题，每小题 3分，共  30分.在每小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑）

1.某人向东行走  5米，记作“+5米”，那么他向西行走  3米，记作

A.“- 3米”    B.“+3米”    C.“- 8米”    D.“+8米”

2.一个不透明的袋中有  4个红球，2个白球，除颜色外完全相同，从中随机摸出一个球是

白球的概率为

A.     B.     C.     D.

3.下列运算错误的是

A.    B.    C.    D.

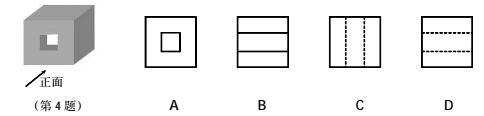
4.如图所示，该几何体的左视图是

5.小敏和小华在某次各科满分均为   100分的期末测试中，各科成绩的平均分相同.小敏想和小华再比较一下两人中谁的各科成绩更加均衡，则他需要分别计算两人各科成绩的

A加权平均数   B方差   C众数   D中位数

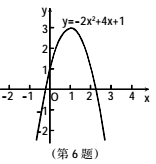6.在求解一元二次方程的两个根x1和x2时，某同学使用电脑软件绘制了如图所示的二次函数的图象，然后通过观察抛物线与x轴的交点，该同学得出- 1<x1<0，2<x2<3的结论.该同学采用的方法体现的数学思想是

A.类比   B.演绎   C.数形结合   D.公理化

7.使不等式 与 同时成立的x的整数值是

A. - 2，- 1，0      B. 0，1       C. - 1，0   D.不存在

8.如图，在直角坐标系 xOy中的三个顶点都在方格纸的格点上，点A的坐标是（-2，0）.将绕点 A顺时针旋转得到，则点 B的对应点的坐标是

A.（1，- 1）   B.（1，1）   C.（- 1，1）   D.（- 1，- 1）

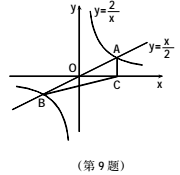
9.如图，正比例函数与反比例函数的图象交于A，B两点，轴于点C，连

接 BC，则的面积为

A.2        B.       C.       D.1

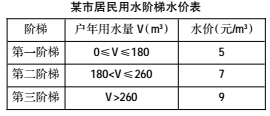10.为引导居民节约用水，某市出台了城镇居民用水阶梯水价制度.每年水费的计算方法为：年交水费=第一阶梯水价*第一阶梯用水量+第二阶梯水价*第二阶梯用水量+第三阶梯水价*第三阶梯用水量.该市某同学家在实施阶梯水价制度后的第一年缴纳水费 1730元，则该同学家这一年的用水量为

A.250m3    B.270m3

C.290m3    D.310m3
非选择题（共90分）

二、填空题（本大题共6个小题，每小题3分，共 18分）

11.计算的结果是       .

12.化简的结果是       .

13.某自然保护区的工作人员，欲估算该自然保护区栖息的某种鸟类的数量.他们首先随机捕捉了500只这种鸟，做了标记之后将其放回，经过一段时间之后，他们又从该保护区随机捕捉该种鸟300只，发现其中20只有之前做的标记，则该保护区有这种鸟类大约       只.

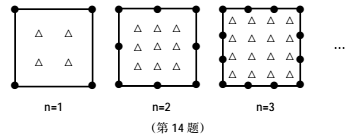
14.如图为一组有规律的图案，则第  n个图案中“”和“”的个数之和为     .（用含n的代数式表示）

15.如图，AB是的直径，内接于，若，则=     .

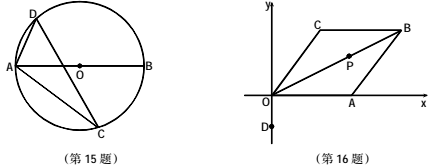
16.如图，在平面直角坐标系xOy中，菱形OABC的顶点A在x轴上，顶点B的坐标为（8，4），点 P是对角线OB上一个动点，点D的坐标为（0，-2），当DP与AP之和最小时，点 P的坐标为     .

三、解答题（本大题共 8个小题，共72分.解答应写出文字说明、证明过程或演算步骤）

17.（每小题 5分，共 10分）

（1）计算：

（2）先化简，再求值：（x+1）（x- 1）- x（x- 2），其中 x=3.

（2）该校决定从预赛中获得优秀等级的三名教师中随机选取两名参加市教育局举办的

课堂教学技能大赛，已知三名教师中有两名男教师、一名女教师.请用树状图或列表

法说明该校选中一男一女教师参加市教育局举办的课堂教学技能大赛的概率.

18.（本题 6分）阅读下列材料，并按要求完成相应的任务.

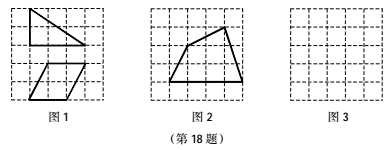
你知道“皮克定理”吗？一张方格纸上，画着纵横两组平行线，相邻平行线之间的距离都等于单位1，这样两组平行线的交点，就是所谓的格点.一个多边形的顶点如果全是格点，这个多边形就叫做格点多边形.有趣的是，这种格点多边形的面积计算起来很方便，只要数一下图形边线上的点的数目及图内的点的数目，就可用公式算出.即，其中a表示多边形内部的点数，b表示多边形边界上的点数，S表示多边形的面积（利用图1中的三角形、四边形可以验证）.这个公式是奥地利数学家皮克在1899年发现的，被称为“皮克定理”.

任务：

（1）如图 2，是的正方形网格，且小正方形的边长为1，利用“皮克定理”可以求出图中格点多边形的面积是       .

（2）已知：一个格点多边形的面积 S为 15，且边界上的点数 b是内部点数a的2倍，则a+b=       ；

（3）请你在图 3中设计一个格点多边形（.要求：①格点多边形的面积为8；②格点多边形是一个轴对称图形但不是中心对称图形.）

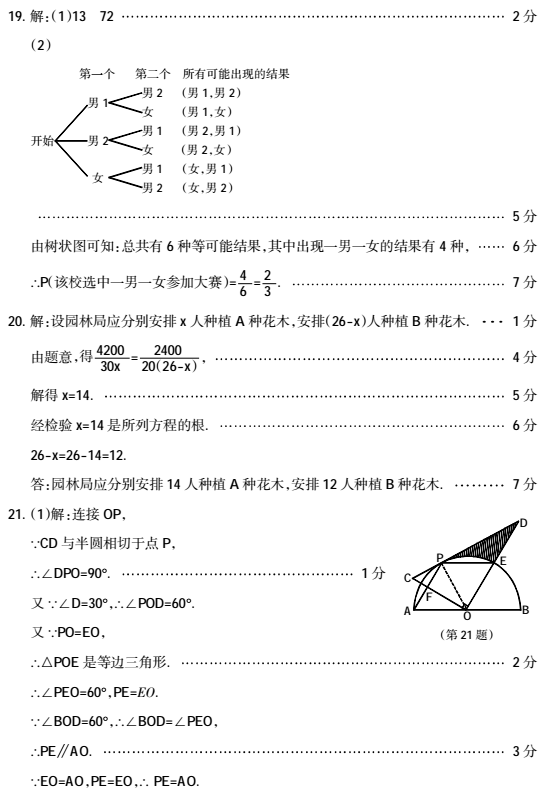
19.（本题 7分）为践行社会主义核心价值观，某市教育局准备举办教师“敬业杯”课堂教学技能大赛，参赛选手均由辖区内各个学校选派.某校首先在校内组织部分教师进行了预赛，并将预赛成绩绘制成了如下不完整的统计图表，请根据图表回答下列问题：

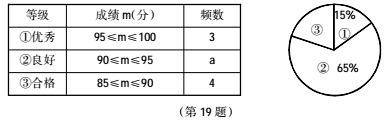
（1）表格中 a的值为      ，扇形统计图中，表示类别③的扇形的圆心角度数为    度；

（2）该校决定从预赛中获得优秀等级的三名教师中随机选取两名参加市教育局举办的课堂教学技能大赛，已知三名教师中有两名男教师、一名女教师.请用树状图或列表法说明该校选中一男一女教师参加市教育局举办的课堂教学技能大赛的概率.

20.（本题 7分）某市园林局准备种植A种花木4200棵，B种花木2400棵.现计划安排26人同时种植这两种花木，已知每人每天能种植 A种花木30棵或 B种花木20棵，则应分别安排多少人种植这两种花木，才能确保同时完成各自的任务？

21.（本题 9分）如图，在中，，，斜边CD与以AB为直径，O为圆心的半圆相切于点P，OD与半圆交于点 E，连接 PA，PE，PA与OC交于点F.

猜想与证明：

（1）当时，试判断四边形 AOEP的形状，并证明；

探索与发现：

（2）当 AB=6时，求图中阴影部分的面积；

（3）若不再添加任何辅助线和字母，请写出图中两组相等的线段. （半径除外）

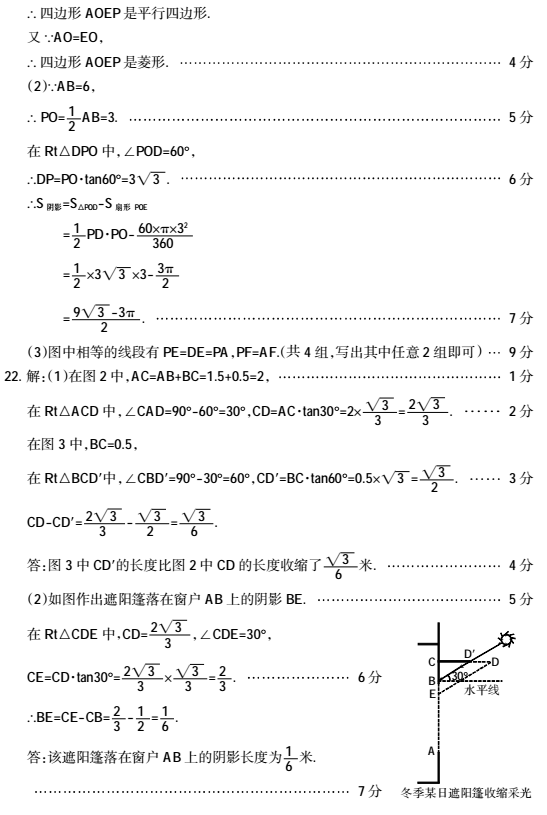
22.（本题 7分）如图1，某同学家的一面窗户上安装有遮阳篷.图2和图3是截面示意图，CD是遮阳篷，窗户 AB为1.5米，BC为0.5米.该遮阳篷有伸缩功能.如图2，该同学在夏季某日的正午时刻测得太阳光和水平线的夹角为，遮阳篷 CD正好将进入窗户 AB的阳光挡住；如图3，该同学在冬季某日的正午时刻测得太阳光和水平线的夹角为，将遮阳篷收缩成 CD'时，遮阳篷正好完全不挡进入窗户 AB的阳光.

（1）计算图 3中CD'的长度比图 2中CD的长度收缩了多少米；（结果保留根号）

（2）如果图 3中遮阳篷的长度为图2中CD的长度，请计算该遮阳篷落在窗户AB上的阴影长度为多少米？（请在图 3中画图并标出相应字母，然后再计算）

23.（本题 13分）综合与探究

如图1，在平面直角坐标系xOy中，抛物线与x轴交于A，B两点（A点在B点左侧），与 y轴交于点C，且点 B的坐标为（4，0）.点E（m，0）为x轴上的一个动点，过点 E作直线轴，与抛物线交于点  F，与直线AC交于点G.

（1）分别求抛物线和直线AC的函数表达式；

（2）当- 8<m<0时，求出使线段 FG的长度为最大值时m的值；

（3）如图 2，作射线 OF与直线 AC交于点P，请求出使时m的值.

24.（本题 13分）综合与实践：折纸中的数学

数学活动课上，老师组织各学习小组同学动手操作，大胆猜想并加以验证.

动手操作：如图，将长与宽的比是的矩形纸片ABCD对折，使得点 B与点A重合，点 C与点 D重合，然后展开，得到折痕EF.BC边上存在一点 G，将角 B沿GH折叠，点B落到 AD边上的点B'处，点 H在AB边上；将角C沿GD折叠，点C恰好落到 B'G上的点C'处. HG和DG分别交EF于点M和点 N，B'G交 EF于点O，连接 B'M，B'N.

提出猜想：①“希望”小组猜想：；

②“奋斗”小组猜想：；

③“创新”小组猜想：四边形 B'MGN是矩形.

独立思考：（1）请你验证上述学习小组猜想的三个结论；（写出解答过程）

（2）假如你是该课堂的一名成员，请你在现有图形中，找出一个和四边形 B忆MGN面积相等的四边形（.直接写出其名称，不必证明）