请选择
返回
请点击全屏查看
2017荆门市中考数学模拟试题
数 学 试 卷
说明：
1. 全卷分两部分，第一部分为选择题，第二部分为非选择题，考试时间120分钟，满分120分．
2．本卷试题，考生必须在答题卡上按规定作答；凡在试卷、草稿纸上作答的，其答案一律无效，答题卡必须保持清洁，不能折叠．
3．选择题1-12题，每小题选出答案后，用2B铅笔将答题卡选择题对应题目的答案标号涂黑；非选择题13-24题，答案（含作辅助线）必须用规定的笔，按作答题目序号，写在答题卡对应的答题区内．
第一部分 选择题
选择题（本大题共12小题，每小题3分，共36分）
1．（2017荆门数学）用配方法解一元二次方程
，配方后的方程是
A．
B．
C．
D．
2．已知AB是⊙O的一条弦，∠AOB＝150°，则AB所对的圆周角为
A．75° B．90° C．105° D．75°或105°
3．将抛物线
向左平移2个单位长度，再向下平移3个单位长度,得到的抛物线对应的函数表达式为
A．
B．
C．
D．
4．（2017荆门数学）在半径为10cm的⊙O中，点P是⊙O内一点，且OP＝6cm，则过点P的最短弦长是
A．8cm B．6cm C．12cm D．16cm
在平面直角坐标系中，已知点
,
，以原点O为位似中心，相似比为
，
把△ABO缩小，则点A的对应点
的坐标是
A．
B．
C．或
D．或
已知反比例函数
图象上有三点
，
，
,则a、b、c的大
小关系是
A．
B．
C．
D．
7．（2017荆门数学）已知
的一条直角边
，另一条直角边
，则以AB为轴旋转一周，所得到的圆锥的表面积是
A．
B．
C．
D．
8. 如图，AD是△ABC的高，AE是△ABC的外接圆⊙O的直径，
且
，则⊙O的直径AE等于
A．
B．6
C．
D．8
如图，一次函数
和反比例函数
的图象
相交于A,B两点，那么关于
的不等式
的解集为
A．
或
B．
或
C．或
D．
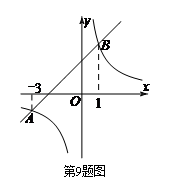
10．（2017荆门数学）把一副三角板如图甲放置，其中∠ACB=90°，∠A=45°，∠D=30°，斜边AB=12，DC=14，把三角板DCE绕着点C顺时针旋转15°得到△
（如图乙），此时线段
的长度为
A．
B． 8 C．10 D．
11．如图，
中，
，以
为直径的⊙O交
于点
,过点C作
∥
,在上取一点
,使
，连接
,对于下列结论：①
；②
∽
；③
；④
为⊙O 的切线.正确的结论是
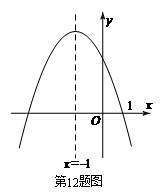A．①② B．①②③ C．①④ D．①②④
12．（2017荆门数学）二次函数
的图象如图所示，给出下列四个结论：
①
；②
；③
；④
，
其中结论错误的个数是
A．4个 B．3个 C．2个 D．1个
第二部分 非选择题
二、填空题（本大题共5小题，每小题3分，共15分）
13．已知关于
的一元二次方程
有两个不相同的实数根,则
的取值范围是 ▲ ．
14．如图，点D在⊙O的直径AB的延长线上，点C在⊙O上，且AC=CD，∠ACD=120°，CD是⊙O的切线，若⊙O的半径为3，则图中阴影部分的面积为 ▲ ．
15．一个不透明的盒子里有4个(除颜色外)完全相同的小球，其中每个小球上分别标有1，-1，-2，-3四个不同的数字，每次摸球前先将盒子里的球摇匀，任意摸出一个球记下数字后再放回盒子，那么两次摸出的小球上两个数字乘积是负数的概率是 ▲ ．
16．（2017荆门数学）如图，在平面直角坐标系中，直线
与
轴、
轴分别交于A,B两点，以AB为
边在第二象限作正方形ABCD，点D在曲线
上．将正方形沿x轴正方向平移
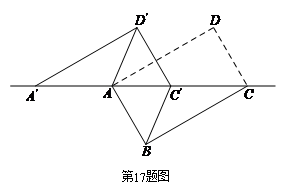a个单位长度后，点C恰好落在该曲线上，则a的值是 ▲ ．
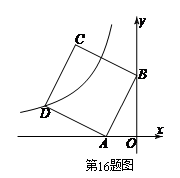
如图，将矩形ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△
，连接
,
．若∠ACB=30°，AB=2，
，△ACD与△
重叠部分的面积为
，则下列结论：①△
≌△
；
②当
时，四边形
是菱形；
③
；其中正确的有 ▲ （填序号）．
三、解答题（本大题共7小题，共69分）
18．（2017荆门数学）（本题满分8分）解下列方程：
（1）
； （2）
.
19．（本题满分9分）某中学组织学生开展社会实践活动，调查社区居民对消防知识的了解程度；记A:特别熟悉，B:有所了解，C:不知道，在某社区随机抽取了100名居民进行问卷调查，将调查结果制成如图所示的统计图，根据统计图解答下列问题：
（1）若该社区有居民1000人，试估计该社区对消防知识“特别熟悉”的居民人数；
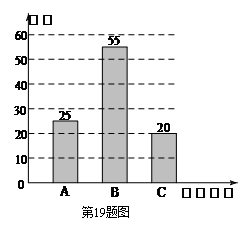（2）该社区的管理人员有男，女各2名，若从中选2名参加消防知识培训，试用列表或画树状图的方法，求恰好选中一男一女的概率．
20．（本题满分10分）如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，∠PBA=∠C．
(1)求证：PB是⊙O的切线；
(2)若OP∥BC，且OP=12，BC=3．求⊙O的半径．
21.（2017荆门数学）（本题满分10分）如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，A，C
分别在坐标轴上，点B的坐标为
，直线
分别交AB，BC于点M，N，反
比例函数
的图象经过点M，N,连接OM，ON．
（1）求反比例函数的解析式；
（2）若点P在
轴上，且△OPM的面积与四边形BMON的面积相等，求点P的坐标．
22．（2017荆门数学）（本题满分10分）已知
是关于
的一元二次方程
的两实数根．
（1）若
，求m的值；
（2）若等腰△ABC的一边长为2，恰好是等腰△ABC另外两边的长，求这个三角形的周长
．
23．（2017荆门数学）（本题满分10分）某工厂生产的一种产品，每件成本是60元，现投放市场进行试销．据市场调查，销售单价是90元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件（要求销售单价不得低于成本）．
（1）求出每天的销售利润y（元）与销售单价x（元）之间的函数关系式；
（2）求出销售单价为多少时，每天的销售利润最大？最大利润是多少？
（3）如果该企业要使该产品每天的销售利润不低于1500元，且每天的总成本不超过6000元，那么销售单价应控制在什么范围？（每天的总成本=每件成本×每天的销售量）
24．（2017荆门数学）（本题满分12分）如图，抛物线
与x轴交于
两点（点
在点
的左侧），与y轴交于点
；
是抛物线的顶点．
（1）求A、B、C的坐标；
（2）点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线BC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N．若点P在点Q右边，当矩形PQNM的周长最大时，求△BEM的面积；
（3）在（2）的条件下，当矩形PMNQ的周长最大时，连接DQ．过抛物线上一点F作y轴的平行线，与直线BC交于点G（点G在点F的上方）．若FG=
DQ，求点F的坐标．