请选择
返回
各位同学在查看时请点击全屏查看
2018年吕梁中考数学冲刺试题
考试时间：120分钟 试卷满分：150分
※ 注意事项：
考生答题时，必须将答案写在答题卡上，答案写在试卷上无效。
1、选择题（每小题3分，共30分）
1．方程 ① 7x2－8x＝1 ② 2x2－5xy＋6y2＝0 ③ 5x2－
－1＝0 ④ 
＝3y中是一元二次方程的为( ▲ )
A．①、② B．①、③ C．①、②、③ D．①、④
2．一元二次方程
的根是( ▲ )
A．
B．
C．
D．
3．已知
是方程
的一个根，则
的值为( ▲ )
A．5 B．﹣5 C．6 D．﹣6
4．抛物线
的顶点位于 ( ▲ )
A．第一象限 B．第二象限 C．第三象限 D．第四象限
5．某商品经过两次连续降价，每件售价由原来的100元降到了64元．设平均每次降价的百分率为x，则下列方程中正确的是( ▲ )
A．100（1+x）2=64 B．64（1+x）2=100 C．64（1﹣x）2=100 D．100（1﹣x）2=64
6．将抛物线y=x2向右平移1个单位长度，得到抛物线的解析式是( ▲ )
A．y=（x+1）2 B．y=（x﹣1）2 C．y=x2+1 D．y=x2﹣1
7．已知抛物线y=x2﹣x﹣2与x轴的一个交点为（m，0），则代数式m2﹣m+2013的值为( ▲ )
A．2013 B．2014 C．2015 D．2016
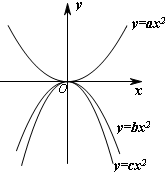
8．抛物线
、
、
的图象如图所示，则
、
、
的大小关系是( ▲ )
A．
＞＞ B．＞＞ C．＞＞ D．＞＞
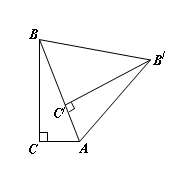
9．如图，在△ABC中，∠C=90°，∠BAC=70°，将△ABC绕点A顺时针旋转70°，Ｂ、Ｃ旋转后的对应点分别是B/和C/，连接BB/，则∠BB/C/的度数是( ▲ )
A．35° B．40° C．45° D．50°
10．对称轴为直线x=﹣1的抛物线y=ax2+bx+c如图所示，有下列结论：
①abc＜0；②16a-4b+c＜0；③ax2+bx≥a-b；④3a+c＜0．其中，正确结论的个数是( ▲ )
A． 1 B． 2 C． 3 D． 4
2、填空题（每小题3分，共24分）
11．一元二次方程
的一次项是 ▲ ．
12．抛物线
的顶点坐标是 ▲ ．
13．已知3是一元二次方程x2﹣4x+c=0的一个根，则方程的另一个根是 ▲ ．
14．关于
的一元二次方程
两个实数根的平方和为3，则的值是 ▲ ．
15．如图，二次函数y=ax2+bx+c的图象经过点A（﹣1，0），B（3，0），那么一元二次方程ax2+bx=0的根是 ▲ ．
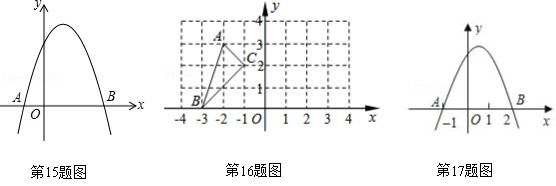
16．如图，△ABC的顶点都在方格线的交点（格点）上，如果将△ABC绕A点按逆时针方向旋转90°，那么点B的对应点B′的坐标是 ▲ ．
17．如图所示，抛物线
与
轴的两个交点分别为A（﹣1，0）和B（2，0），则当
＜0时，的取值范围是 ▲ ．
18．将点A（4,0）绕原点顺时针旋转30°得A1，再将点A1绕原点顺时针旋转30°得A2，再将点A2绕原点顺时针旋转30°得A3，每次都将得到的点绕原点顺时针旋转30°，得到的点依次记为A1、A2、A3···、An，则A100的坐标是 ▲ ．
三、（第19题12分，第20题10分，共计22分）
19．解方程
（1）
（配方法） （2）
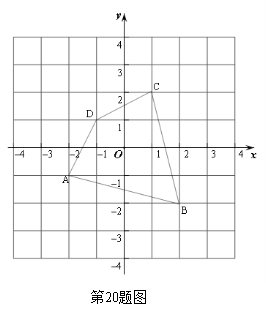
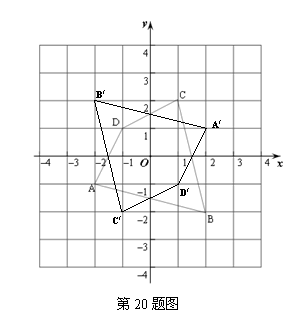
20．如图，将四边形ABCD绕原点O旋转180°得四边形A/B/C/D/.
（1）画出旋转后的四边形A/B/C/D/；
（2）写出A/、B/、C/、D/的坐标；
（3）四边形ABCD和四边形A/B/C/D/组成的图形是轴对称图形吗？若是，请直接写出对称轴的解析式.
四、（第21题12分，第22题12分，共计24分）
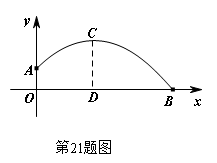
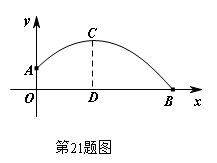
21. 如图所示,一男生推铅球,铅球在点A处出手,出手时铅球离地面
m.铅球落地点在B处,铅球运行中在该男生前4 m处(即0D=4)达到最高点,此时铅球离地面3 m.根据图示的直角坐标系,你能算出该男生推铅球的成绩吗?
22. 抛物线上部分点的横坐标
，纵坐标
的对应值如下表：
| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
（1）根据上表填空：
① 抛物线与
轴的交点坐标是 ▲ 和 ▲ ；
② 抛物线经过点（
， ▲ ）；
③ 抛物线的对称轴是直线 ▲ ；
④ 在对称轴右侧，
随
增大而 ▲ .
（2）试确定抛物线的解析式.
5、解答题（12分）
23．将一条长为20cm的铁丝剪成两段，并以每一段铁丝的长度为周长做成一个正方形．
（1）要使这两个正方形的面积之和等于13cm2，那么这段铁丝剪成两段后的长度分别是多少？
（2）两个正方形的面积之和可能等于12cm2吗？若能，求出两段铁丝的长度；若不能，请说明理由．
六、解答题（12分）
24. 某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于50%，经试销发现，销售量y(件)与销售单价x（元）的关系符合一次函数y=-x+140.
（1）直接写出x的取值范围；
（2）若销售该服装获得利润为W元，试求W与x之间的函数关系式，销售单价定为多少时，可获得最大利润，最大利润是多少元？
（3）若获得利润恰好为1200元，则此时的销售单价是多少？
七、解答题（12分）
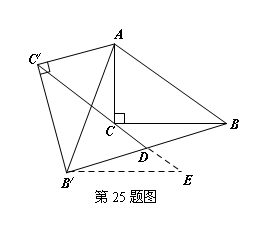
25. 如图，在△ABC中，∠ACB=90°，将△ABC绕点A顺时针旋转，Ｂ、Ｃ旋转后的对应点分别是B/和C/，连接C/C并延长交BB/于点D.
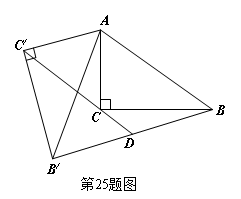（1）求证：
BCD=B/C/D；
（2）求证：BD=B/D.
八、解答题（14分）
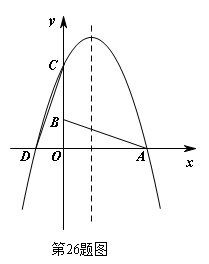
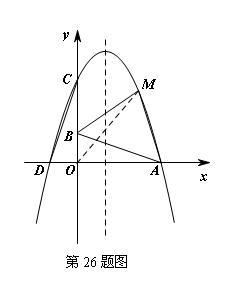
26. 如图，已知，A点坐标是（3,0），B点坐标是（0,1），将△AOB绕点O逆时针旋转90°得到△COD，A、B旋转后的对应点分别为C和D，抛物线
经过C、D两点.
（1）求抛物线的解析式；
（2）点M在第一象限抛物线上，△ABM的面积等于4，求点M的坐标；
（3）点Q是抛物线上的动点，在对称轴上是否存在点P，使得以A、B、P、Q为顶点的四边形为平行四边形，若存在，请直接写出点P的坐标；若不存在，请说明理由.
2018年吕梁中考数学冲刺试题参考答案
一、选择题（每小题3分，共30分）
1.D 2.D 3.A 4.B 5.D 6.B 7.C 8.A 9.A 10.C
二、填空题（每小题3分，共24分）
- -3x 12.（1，-2） 13.1 14.-1
15.
16.（1,2） 17. 
＜-1或＞2 18.
三、（第19题12分，第20题10分，共计22分）
19．解方程
（1）解：移项，得 
--------------------------------------------------1
系数化为1，得 ------------------------------------------------2
配方，得 -------------------------------------3
-------------------------------------------4
由此可得 -------------------------------------------------5
----------------------------------6
（2）解：
---------------------------------------------------1
--------------------------------------------------------3
或
------------------------------------------------------4
----------------------------------------------------------6
20.（1）画图正确------------------------------------------------------------------------------------------3
（2）A/（2,1）、B/（-2，2) 、 C/（-1,-2）、 D/ （1，-1）----------------------------------7
（3）四边形ABCD和四边形A/B/C/D/组成的图形是轴对称图形---------------------------8
对称轴的解析式是y=x和y=-x----------------------------------------------------------------10
四、（第21题12分，第22题12分，共计24分）
21.
解：能算出该男生推铅球的成绩-----------------------------------------------1
由题意得，抛物线的顶点坐标是（4,3），且此抛物线经过（0，
）------------------------3
设抛物线的解析式是
--------------------------------------------------------------4
-----------------------------------------------------------------------------------------5
解得
----------------------------------------------------------------------------------------------7
∴
--------------------------------------------------------------------------------9
令y=0，得
------------------------------------------------------------------------11
∴B（10,0）
答：男生推铅球的成绩是10米.--------------------------------------------12
22.（1）
① （-2,0），（1,0）-------------------------------------------------------------2
② 8--------------------------------------------------------------------------------3
③
-----------------------------------------------------------------------4
④增大----------------------------------------------------------------------------5
（2）∵抛物线
经过（-2,0），（0-4），（1,0）三点
∴
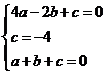----------------------------------------------------------------------8
解得：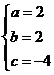
---------------------------------------------------------------------------11
∴抛物线的解析式是
--------------------------------------------12
6、解答题（12分）
23．
解：设一个正方形的边长为
cm，则另一个正方形的边长为（
）cm-------------1
（1）依题意得
------------------------------------------------------------------4
化简得
--------------------------------------------------------------------------------5
解得
--------------------------------------------------------------------------------------7
答：铁丝剪成两段的长度为8cm和12cm.-----------------------------------------------------8
（2）两个正方形的面积之和不可能等于12cm2------------------------------------------9
∵
---------------------------------------------------------------------------10
△=
＜0--------------------------------------------------------------11
原方程无实数根，所以两个正方形的面积之和不可能等于12cm2----------------12
（或利用二次函数求面积的最小值为12.5cm2，说明面积之和不可能等于12cm2）
六、解答题（12分）
24.
（1）60≤x≤90----------------------------------------------------------------------------------------2
（2）W=y(x-60)=(-x+140)(x-60)=
----------------------------------------4
W=
∵-1＜0，抛物线开口向下
对称轴为x=100，当x＜100时，W随x的增大而增大---------------------------------------6
∴当x=90时，W有最大值1500--------------------------------------------------------------------7
答：销售单价定为90元时，可获得最大利润，最大利润是1500元.----------------------8
（3）
------------------------------------------------------------------9
解得
＞90，
不合题意，舍去------------------------------------------11
答：此时的销售单价是80元.---------------------------------------------------------------------------12
七、解答题（12分）
25.
证明：
（1）∵AC=AC/
∴
AC/C=ACC/----------------------------------------------------------------------------------2
又∵∠AC/B/=ACB=90°
∴AC/C+B/C/D=90°---------------------------------------------------------------------------3
ACC/+BCD=180°-90°=90°---------------------------------------------------------------4
∴BCD=B/C/D----------------------------------------------------------------------------------5
（2）作B/E∥BC交CD的延长线于E----------------------------------------------------------6
∴BCD=E
∵BCD=B/C/D
∴E=B/C/D-------------------------------------------------------------------------------------7
∴B/E=B/C/--------------------------------------------------------------------------------------------8
在△BCD和△B/ED中
----------------------------------------------------------------------------10
∴△BCD≌△B/ED（AAS）---------------------------------------------------------------------11
∴BD=B/D--------------------------------------------------------------------------------------------12
八、解答题（14分）
26.
解：（1）C（0,3），D（-1,0）------------------------------------------------------------------------2
∵抛物线
经过C、D两点.
∴
---------------------------------------------------------------------------------------3
解得
------------------------------------------------------------------------------------------------4
∴抛物线的解析式是
--------------------------------------------------------------5
（2）设M点坐标为（x,y）
S△ABM=S△OBM+S△AOM-S△AOB=4--------------------------------------------------------------------------6
所以
--------------------------------------------------------------7
=
解得：
-----------------------------------------------------------------------------------8
∴
---------------------------------------------------------------------------------------9
∴
--------------------------------------------------------------------------------10
（3）存在-------------------------------------------------------------------------------------------------11
--------------------------------------------------------------------------14