请选择
2017年广州市中考数学试题【精编解析版】
由于版式的问题,试题可能会出现乱码的现象,为了方便您的阅读请点击全屏查看
第一部分 选择题(共30分)
一、选择题:本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图1,数轴上两点![]() 表示的数互为相反数,则点
表示的数互为相反数,则点![]() 表示的()
表示的()
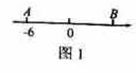
A. -6 B.6 C. 0 D.无法确定
答案:B
解析:-6的相反数是6,A点表示-6,所以,B点表示6。
2.如图2,将正方形![]() 中的阴影三角形绕点
中的阴影三角形绕点![]() 顺时针旋转90°后,得到图形为 ()
顺时针旋转90°后,得到图形为 ()

答案:A
解析:顺时针90°后,AD转到AB边上,所以,选A。
3. 某6人活动小组为了解本组成员的年龄情况,作了一次调查,统计的年龄如下(单位:岁)12,13,14,15,15,15.这组数据中的众数,平均数分别为()
A.12,14 B. 12,15 C.15,14D. 15,13
答案:C
解析:15出现次数最多,有3次,所以,众数为15
平均数为:![]() =14。
=14。
4. 下列运算正确的是()
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
答案:D
解析:因为![]() ,故A错,又
,故A错,又![]() ,B错,
,B错,
因为![]() ,所以,C也错,只有D是正确的。
,所以,C也错,只有D是正确的。
5.关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根,则
有两个不相等的实数根,则![]() 的取值范围是()
的取值范围是()
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
答案:A
解析:根的判别式为△=![]() ,解得:
,解得:![]() 。
。
6. 如图3,![]() 是
是![]() 的内切圆,则点
的内切圆,则点![]() 是
是![]() 的()
的()
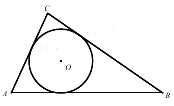 图3
图3
A. 三条边的垂直平分线的交点B.三角形平分线的交点
C. 三条中线的交点 D.三条高的交点
答案:B
解析:内心到三角形三边距离相等,到角的两边距离相等的点在这个角的角平分线上,故选B。
7. 计算![]() ,结果是()
,结果是()
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
答案:A
解析:原式=![]() 。
。
8.如图4,![]() 分别是
分别是![]() 的边
的边![]() 上的点,
上的点,![]() ,将四边形
,将四边形![]() 沿
沿![]() 翻折,得到
翻折,得到![]() ,
,![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的周长为 ()
的周长为 ()
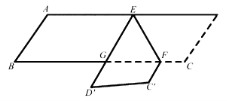
A.6 B. 12 C. 18 D.24
答案:C
解析:因为∠DEF=60°,翻折可知∠FEG=60°,则∠AEG=60°,根据两直线平行内错角相等,∠EGF=∠EFG=60°,所以,△EFG是个等边三角形,所以,选C。
9.如图5,在![]() 中,在
中,在![]() 中,
中,![]() 是直径,
是直径,![]() 是弦,
是弦,![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,则下列说法中正确的是()
,则下列说法中正确的是()
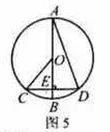
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
答案:D
解析:根据垂径定理可得出弧BC=弧BD,∠BAD和∠COB分别为相等的弧长所对的圆周角和圆心角,由圆周角定理可知,![]() 。
。
10. ![]() ,函数
,函数![]() 与
与![]() 在同一直角坐标系中的大致图象可能是()
在同一直角坐标系中的大致图象可能是()
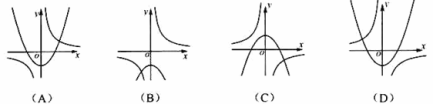
答案:D
解析:如果![]() >0,则反比例函数
>0,则反比例函数![]() 图象在第一、三象限,二次函数
图象在第一、三象限,二次函数![]() 图象开口向下,
图象开口向下,
排除A;二次函数图象与Y轴交点(0,![]() )在y轴正半轴,排除B;
)在y轴正半轴,排除B;
如果![]() <0,则反比例函数
<0,则反比例函数![]() 图象在第二、四象限,二次函数
图象在第二、四象限,二次函数![]() 图象开口向上,
图象开口向上,
排除C;故选D。
第二部分 非选择题(共120分)
二、填空题:本大题共6小题 ,每小题3分,满分18分
11.如图6,四边形![]() 中,
中,![]() ,则
,则![]() ___________.
___________.
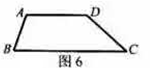
答案:70°
解析:两直线平行,同旁内角互补,可得:![]() 180°-110°=70°
180°-110°=70°
12.分解因式:![]() ___________.
___________.
答案:![]()
解析:原式=![]()
![]()
13.当![]() 时,二次函数
时,二次函数![]() 有最小值______________.
有最小值______________.
答案:1 , 5
解析:二次函数配方,得:![]() ,所以,当x=1时,y有最小值5。
,所以,当x=1时,y有最小值5。
14.如图7,![]() 中,
中,![]() ,则
,则![]() .
.
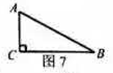
答案:17
解析:因为![]() ,所以,AC=8,由勾股定理,得:AB=17。
,所以,AC=8,由勾股定理,得:AB=17。
15.如图8,圆锥的侧面展开图是一个圆心角为120°的扇形,若圆锥的底面圆半径是![]() ,则圆锥的母线
,则圆锥的母线![]() .
.
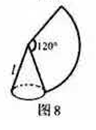
答案:![]()
解析:扇形的弧长和圆锥的底面周长相等,即:![]() ,解得:
,解得:![]() =
=![]()
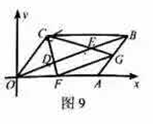
16.如图9,平面直角坐标系中![]() 是原点,
是原点,![]() 的顶点
的顶点![]() 的坐标分别是
的坐标分别是![]() ,点
,点![]() 把线段
把线段![]() 三等分,延长
三等分,延长![]() 分别交
分别交![]() 于点
于点![]() ,连接
,连接![]() ,则下列结论:
,则下列结论:
①![]() 是
是![]() 的中点;②
的中点;②![]() 与
与![]() 相似;③四边形
相似;③四边形![]() 的面积是
的面积是![]() ;④
;④![]() ;其中正确的结论是 .(填写所有正确结论的序号)
;其中正确的结论是 .(填写所有正确结论的序号)
答案:①③
解析:

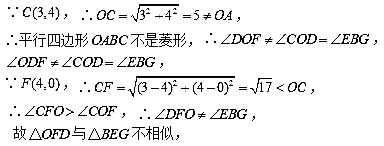
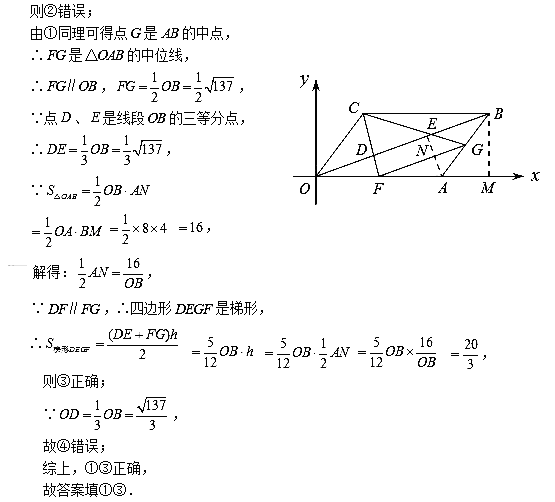
三、解答题 (本大题共9小题,共102分.解答应写出文字说明、证明过程或演算步骤.)
17. 解方程组:![]()
解析:(1)×3,得:![]() =15,减去(2),得x=4
=15,减去(2),得x=4
解得:![]()
18. 如图10,点![]() 在
在![]() 上,
上,![]() .
.
求证:![]() .
.
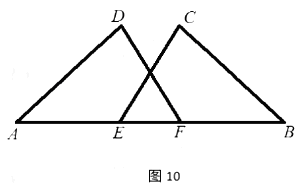
证明:因为AE=BF,所以,AE+EF=BF+EF,即AF=BE,
在△ADF和△BCE中,
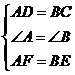
所以,![]()
19.某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间![]() (单位:小时),将学生分成五类:
(单位:小时),将学生分成五类:![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),绘制成尚不完整的条形统计图如图11.
),绘制成尚不完整的条形统计图如图11.

根据以上信息,解答下列问题:
(1)![]() 类学生有_________人,补全条形统计图;
类学生有_________人,补全条形统计图;
(2)![]() 类学生人数占被调查总人数的__________%;
类学生人数占被调查总人数的__________%;
(3)从该班做义工时间在![]() 的学生中任选2人,求这2人做义工时间都在
的学生中任选2人,求这2人做义工时间都在![]() 中的概率.
中的概率.
解析:(1)E类:50-2-3-22-18=5(人),统计图略
(2)D类:18![]() 50×100%=36%
50×100%=36%

20. 如图12,在![]() 中,
中,![]() .
.
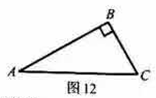
(1)利用尺规作线段![]() 的垂直平分线
的垂直平分线![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() ;(保留作图痕迹,不写作法)
;(保留作图痕迹,不写作法)
(2)若![]() 的周长为
的周长为![]() ,先化简
,先化简![]() ,再求
,再求![]() 的值.
的值.
解析:(1)如下图所示:
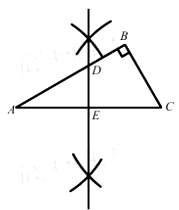

21. 甲、乙两个工程队均参与某筑路工程,先由甲队筑路60公里,再由乙队完成剩下的筑路工程,已知乙队筑路总公里数是甲队筑路总公里数的![]() 倍,甲队比乙队多筑路20天.
倍,甲队比乙队多筑路20天.
(1)求乙队筑路的总公里数;
(2)若甲、乙两队平均每天筑路公里数之比为5:8,求乙队平均每天筑路多少公里.
解析:(1)乙队筑路的总公里数:![]() =80(公里);
=80(公里);

22.将直线![]() 向下平移1个单位长度,得到直线
向下平移1个单位长度,得到直线![]() ,若反比例函数
,若反比例函数![]() 的图象与直线
的图象与直线![]() 相交于点
相交于点![]() ,且点
,且点![]() 的纵坐标是3.
的纵坐标是3.
(1)求![]() 和
和![]() 的值;
的值;
(2)结合图象求不等式![]() 的解集.
的解集.
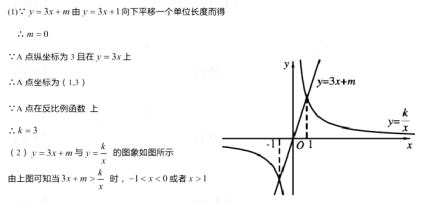
解析:
23.已知抛物线![]() ,直线
,直线![]() 的对称轴与
的对称轴与![]() 交于点
交于点![]() ,点
,点![]() 与
与![]() 的顶点
的顶点![]() 的距离是4.
的距离是4.
(1)求![]() 的解析式;
的解析式;
(2)若![]() 随着
随着![]() 的增大而增大,且
的增大而增大,且![]() 与
与![]() 都经过
都经过![]() 轴上的同一点,求
轴上的同一点,求![]() 的解析式.
的解析式.
解析:


24.如图13,矩形![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() 关于
关于![]() 的对称图形为
的对称图形为![]() .
.
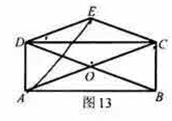
(1)求证:四边形![]() 是菱形;
是菱形;
(2)连接![]() ,若
,若![]() ,
,![]() .
.
①求![]() 的值;
的值;
②若点![]() 为线段
为线段![]() 上一动点(不与点
上一动点(不与点![]() 重合),连接
重合),连接![]() ,一动点
,一动点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿线段
的速度沿线段![]() 匀速运动到点
匀速运动到点![]() ,再以
,再以![]() 的速度沿线段
的速度沿线段![]() 匀速运动到点
匀速运动到点![]() ,到达点
,到达点![]() 后停止运动.当点
后停止运动.当点![]() 沿上述路线运动到点
沿上述路线运动到点![]() 所需要的时间最短时,求
所需要的时间最短时,求![]() 的长和点
的长和点![]() 走完全程所需的时间.
走完全程所需的时间.
解析:


25.如图14,![]() 是
是![]() 的直径,
的直径,![]() ,连接
,连接![]() .
.
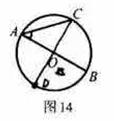
(1)求证:![]() ;
;
(2)若直线![]() 为
为![]() 的切线,
的切线,![]() 是切点,在直线
是切点,在直线![]() 上取一点
上取一点![]() ,使
,使![]() 所在的直线与
所在的直线与![]() 所在的直线相交于点
所在的直线相交于点![]() ,连接
,连接![]() .
.
①试探究![]() 与
与![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
②![]() 是否为定值?若是,请求出这个定值;若不是,请说明理由.
是否为定值?若是,请求出这个定值;若不是,请说明理由.
解析:


