请选择
2017-2018珠海市前山中学考试九年级期中数学试题【word版无答案】
由于版式的问题,试题可能会出现乱码的现象,为了方便您的阅读请点击全屏查看
一、选择题(每小题3分,共30分)
1.将方程![]() 化为一元二次方程的一般形式,其中二次项系数,一次项系数,常数项分别是()
化为一元二次方程的一般形式,其中二次项系数,一次项系数,常数项分别是()
A. 3,-8,-10B.3,-8, 10
C. 3, 8,-10 D. -3 ,-8,-10
用配方法解方程![]() 时,原方程应变形为()
时,原方程应变形为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.在下列四个图案中,不是中心对称图形的是()
A.  B.
B. C.
C. D.
D.
4.将二次函数![]() 的图象先向右平移1个单位,再向上平移1个单位后顶点为()
的图象先向右平移1个单位,再向上平移1个单位后顶点为()
A.(1,3) B.(2,-1) C.(0,-1) D.(0,1)
5.如图5,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为()
A.35° B.40° C.50° D.65°
6.图6(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图6(2)建立平面直角坐标系,则抛物线的关系式是()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()

![]()
7.已知三角形两边长分别为2和9,第三边长为二次方程![]() 的一根, 则这个三角形的周长为
的一根, 则这个三角形的周长为
A.11 B.17 C.17或19 D.19
8.已知二次函数![]() 的图象和
的图象和![]() 轴有交点,则
轴有交点,则![]() 的取值范围是()
的取值范围是()
A.![]() B.
B. ![]() ≥
≥![]() 且
且![]() C.
C.![]() ≥
≥![]() D.
D.![]() 且
且![]()
9.已知点A的坐标为![]() ,O为原点,连结OA,将线段OA绕点O按逆时针方向旋转90°得OA1,则点A1的坐标为()
,O为原点,连结OA,将线段OA绕点O按逆时针方向旋转90°得OA1,则点A1的坐标为()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10.在平面直角坐标系中,二次函数y=a(x-h)2(a≠0)的图象可能是()
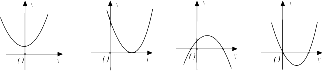
A B C D
二、填空题(每小题4分,共24分)
11. 若点![]() 与点
与点![]() 是关于原点
是关于原点![]() 对称,则点
对称,则点![]() 的坐标为 .
的坐标为 .
12. 二次函数![]() 的顶点坐标为 .
的顶点坐标为 .
13. 关于![]() 的一元二次方程
的一元二次方程![]() 有实数根,则
有实数根,则![]() 的取值范围
的取值范围
为_________.
14. 已知抛物线![]() 与
与![]() 轴的公共点是(-4,0),(2,0),则这条抛
轴的公共点是(-4,0),(2,0),则这条抛
物线的对称轴是直线__ _.
15.如图,将矩形![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后,得到
后,得到
矩形![]() ,如果
,如果![]() ,那么
,那么![]() .
.
 16.如图,二次函数
16.如图,二次函数![]() 的图象与y轴正半轴相交,其顶点坐标
的图象与y轴正半轴相交,其顶点坐标
为![]() ,下列结论:①ac<0;②b<0;③4ac-b2<0;④a+b+c<0.
,下列结论:①ac<0;②b<0;③4ac-b2<0;④a+b+c<0.
其中正确的有________.(填序号)
三、解答题:(共3题,每题6分,共18分)
17.解方程 ![]() . 18. 解方程
. 18. 解方程 ![]() .
.
19.某种品牌的手机经过四、五月份连续两次降价,每部售价由2500元降到了1600元.求平均每月降价的百分率.
四、解答题:(共3题,每题7分,共21分)

20.如图, (1)分别写出A,B两点的坐标;
(2)将△ABC绕点A顺时针旋转90°,
画出旋转后的△AB1C1.
21. 在一块长16m、宽12m的矩形荒地上,小明要建造一个花园,并使花园所占的面积为荒地面积的一半,其中花园四周小路的宽度都相等,求小路的宽.

22. 已知二次函数中![]() 和
和![]() 的部分对应值如下表:
的部分对应值如下表:
| … | -1 | 0 | 1 | 2 | 3 | … |
| … | 0 | -3 | -4 | -3 | 0 | … |
(1)求二次函数的解析式;
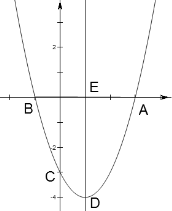
(2)如图,![]() 、
、![]() 、
、![]() 为抛物线与坐标轴的交点,
为抛物线与坐标轴的交点,
点![]() 为抛物线的顶点,抛物线的对称轴
为抛物线的顶点,抛物线的对称轴![]() 上存在一点
上存在一点![]() ,
,
使得![]() 的值最小.求出点
的值最小.求出点![]() 坐标.
坐标.
五、解答题:(共3题,每题9分,共27分)
23. ![]() 表示n边形的对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么
表示n边形的对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么![]() 与n的关系式是:
与n的关系式是:
![]() (其中,a,b是常数,n≥4)
(其中,a,b是常数,n≥4)
⑴通过画图,可得四边形时,![]() =(填数字);五边形时,
=(填数字);五边形时,![]() =(填数字).
=(填数字).
⑵请根据四边形和五边形对角线交点的个数,结合关系式,求![]() 的值.
的值.
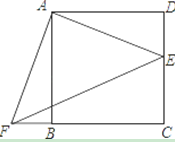
24. 如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针
旋转到△ABF的位置.
(1)旋转中心是点,旋转角度是度;
(2)若连结EF,则△AEF是三角形;并证明;
(3)若四边形AECF的面积为25,DE=2,求AE的长.
25. 已知:如图,抛物线![]() (
(![]() )与y轴交于C点,与x轴交于A、B两点,A点在B点左侧.点B的坐标为(1,0),OC=3BO.
)与y轴交于C点,与x轴交于A、B两点,A点在B点左侧.点B的坐标为(1,0),OC=3BO.
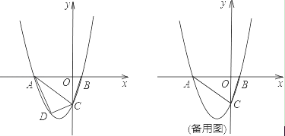
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.