请选择
2018年佛山中考九年级数学模拟试题【精编解析版】
由于版式的问题,试题可能会出现乱码的现象,为了方便您的阅读请点击全屏查看
一、选择题:(每小题2分,共20分)
1.关于x的方程ax2﹣3x+(a﹣2)=0是一元二次方程,则()
A.a>0 B.a≠0 C.a=0 D.a≥0
2.关于x的一元二次方程(3﹣x)(3+x)﹣2a(x+1)=5a的一次项系数是()
A.8a B.﹣8a C.2a D.7a﹣9
3.方程2x(x﹣3)+3=0的二次项系数、一次项系数及常数项的和是()
A.3 B.2 C.﹣1 D.﹣3
4.若x=2是关于x的一元二次方程x2+x+m=0的一个根,则m是()
A.6 B.3 C.﹣6 D.﹣3
5.若方程x2+3x+b2﹣16=0和x2+3x﹣3b+12=0的解相同,则b的值为()
A.4 B.﹣7 C.4或﹣7 D.所有实数
6.用配方法解方程3x2﹣![]() x﹣1=0时,变形正确的是()
x﹣1=0时,变形正确的是()
A.(x+![]() )2﹣
)2﹣![]() =0 B.3(x+
=0 B.3(x+![]() )2﹣
)2﹣![]() =0
=0
C.(x﹣![]() )2﹣
)2﹣![]() =0 D.3(x﹣
=0 D.3(x﹣![]() )2﹣
)2﹣![]() =0
=0
7.关于x的方程[mx2﹣(m﹣n)x﹣n](x2﹣6x+12)=0(其中m、n是实数,且m≠0)共有()个不等实根.
A.2 B.3 C.4 D.1或2
8.某市快乐公园有一长方形的花园,长为400米,宽为300米,现准备在其四周铺设一条等宽的休闲小路,所增加的面积为花园面积的![]() ,则此休闲小路的宽是()
,则此休闲小路的宽是()
A.4米 B.5米 C.8米 D.10米
9.已知k≠1,一元二次方程(k﹣1)x2+kx+1=0有根,则k的取值范围是()
A.k≠2 B.k>2
C.k<2且k≠1 D.k为一切不是1的实数
10.对于一元二次方程ax2+bx+c=0(a≠0),有下列说法:
①当a<0,且b>a+c时,方程一定有实数根;
②若ac<0,则方程有两个不相等的实数根;
③若a﹣b+c=0,则方程一定有一个根为﹣1;
④若方程有两个不相等的实数根,则方程bx2+ax+c=0一定有两个不相等的实数根.
其中正确的有()
A.①②③ B.①②④ C.②③ D.①②③④
二、填空题:((每小题3分,共24分)
11.关于x的方程(a2﹣1)x2+2(a﹣1)x+2a+2=0,当a 时,为一元一次方程.当a 时,为一元二次方程.
12.已知x=1是一元二次方程x2+mx+n=0的一个根,则m2+2mn+n2的值为 .
13.已知关于x的一元二次方程2x2﹣x﹣k=0有两个相等的实数根,则k的值为 .
14.若![]() ,则以x,y的值为两边长的等腰三角形的周长是 .
,则以x,y的值为两边长的等腰三角形的周长是 .
15.实数a、b满足(a+b)2+a+b﹣2=0,则(a+b)2的值为 .
16.若关于x的方程x2﹣(m+5)|x|+4=m恰有3个实数解,则实数m= .
17.根据题意列一元二次方程:有10个边长均为x的正方形,它们的面积之和是200,则有 .
18.如果25x2﹣(k﹣1)xy+9y2是一个完全平方式,那么K的值为 .
三.解一元二次方程(每小题24分,共24分)
19.(24分)(1)x2=64
(2)5x2﹣![]() =0
=0
(3)(x+5)2=16
(4)8(3﹣x)2﹣72=0
(5)2y=3y2
(6)2(2x﹣1)﹣x(1﹣2x)=0
(7)3x(x+2)=5(x+2)
(8)(1﹣3y)2+2(3y﹣1)=0.
四.解方程解应用题(共32分,20----22题每题6分,23---24题每题7分)
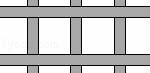
20.(6分)如图,有一块长为30米,宽为10米的长方形菜地,在菜地里要留出南北三条,东西两条,宽度一样的小路,并使实际种植面积为216平方米,求小路的宽应为几米.
21.(6分)某商店将进价为16元的商品按每件20元售出,每天可售出300件,现在采取提高商品售价减少销售量的办法增加利润.若这种商品每件的销售价每提高1元其销售量就减少20件,问每件售价定为多少元时,才能使每天利润为1680元,且销售量较少?
22.(6分)有一间长18米,宽7.5米的会议室,在它的中间铺一块地毯,地毯的面积是会议室面积的一半,且四周未铺地毯外的宽度相同,求四周所留的宽度是多少米?
23.(7分)一件上衣,每件原价500元,第一次降价后,销售甚慢,于是再次进行大幅降价,第二次降价的百分率是第一次降价的百分率的2倍,结果这批上衣以每件240元的价格迅速售出,求两次降价的百分率各是多少.
24.(7分)汽车租赁公司共有出租车120辆,每辆汽车的日租金为160元,出租业务供不应求,为适合市场需求,经有关部门批准,公司准备适当提高日租金,经市场调查发现,一辆汽车的日租金每增加10元,每天出租的汽车相应的减少6辆,若不考虑其他因素,一辆汽车的日租金提高几个10元时,才能使公司的日租金收入最高?公司的日租金总收入比提高租金前增加了多少?(公司日租金总收入=每辆汽车的日租金×公司每天出租的汽车数)
2018年佛山中考九年级数学模拟试题参考答案与试题解析
一、选择题:(每小题2分,共20分)
1.(2分)关于x的方程ax2﹣3x+(a﹣2)=0是一元二次方程,则()
A.a>0 B.a≠0 C.a=0 D.a≥0
【分析】根据一元二次方程的定义解答,一元二次方程必须满足四个条件:未知数的最高次数是2;二次项系数不为0;是整式方程;含有一个未知数.
【解答】解:关于x的方程ax2﹣3x+(a﹣2)=0是一元二次方程,得a≠0,
故选:B.
【点评】本题考查了一元二次方程的概念,判断一个方程是否是一元二次方程,首先要看是否是整式方程,然后看化简后是否是只含有一个未知数且未知数的最高次数是2.
2.(2分)关于x的一元二次方程(3﹣x)(3+x)﹣2a(x+1)=5a的一次项系数是()
A.8a B.﹣8a C.2a D.7a﹣9
【分析】首先利用乘法公式整理,求出一次项系数即可.
【解答】解:∵(3﹣x)(3+x)﹣2a(x+1)=5a,
∴9﹣x2﹣2ax﹣2a=5a,
∴x2+2ax+7a﹣9=0,
∴一次项系数是:2a.
故选:C.
【点评】此题主要考查了一元二次方程的一般形式,正确利用乘法公式整理是解题关键.
3.(2分)方程2x(x﹣3)+3=0的二次项系数、一次项系数及常数项的和是()
A.3 B.2 C.﹣1 D.﹣3
【分析】方程整理为一般形式,找出a,b,c的值即可.
【解答】解:方程整理得:2x2﹣6x+3=0,
则二次项系数、一次项系数及常数项的和为2﹣6+3=﹣1.
故选C
【点评】一元二次方程的一般形式是:ax2+bx+c=0(a,b,c是常数且a≠0)特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.在一般形式中ax2叫二次项,bx叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项.
4.(2分)若x=2是关于x的一元二次方程x2+x+m=0的一个根,则m是()
A.6 B.3 C.﹣6 D.﹣3
【分析】把x=2代入方程,可得关于m的一元一次方程,解方程即可.
【解答】解:把x=2代入方程,得
4+2+m=0,
解得m=﹣6.
故选C.
【点评】本题考查了一元二次方程的解的意义:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.解题的关键是把x=2代入方程.
5.(2分)若方程x2+3x+b2﹣16=0和x2+3x﹣3b+12=0的解相同,则b的值为()
A.4 B.﹣7 C.4或﹣7 D.所有实数
【分析】根据方程解相同,得到常数项相等即可求出b的值.
【解答】解:根据题意得:b2﹣16=﹣3b+12,即b2+3b﹣28=0,
分解因式得:(b﹣4)(b+7)=0,
解得:b=4或﹣7,
当b=﹣7时,两方程为x2+3x+33=0无解,舍去,
则b=4.
故选A
【点评】此题考查了一元二次方程的解,方程的解即为能使方程左右两边相等的未知数的值.
6.(2分)用配方法解方程3x2﹣![]() x﹣1=0时,变形正确的是()
x﹣1=0时,变形正确的是()
A.(x+![]() )2﹣
)2﹣![]() =0 B.3(x+
=0 B.3(x+![]() )2﹣
)2﹣![]() =0
=0
C.(x﹣![]() )2﹣
)2﹣![]() =0 D.3(x﹣
=0 D.3(x﹣![]() )2﹣
)2﹣![]() =0
=0
【分析】等式左边配方时,可先提取二次项系数,然后将括号内进行配方,就可解决问题.
【解答】解:∵3x2﹣![]() x﹣1=3(x2﹣
x﹣1=3(x2﹣![]() x)﹣1
x)﹣1
=3(x2﹣![]() x+
x+![]() ﹣
﹣![]() )﹣1
)﹣1
=3[(x﹣![]() )2﹣
)2﹣![]() )]﹣1
)]﹣1
=3[(x﹣![]() )2﹣
)2﹣![]() ﹣1
﹣1
=3(x﹣![]() )2﹣
)2﹣![]() ,
,
∴方程3x2﹣![]() x﹣1=0可变形为3(x﹣
x﹣1=0可变形为3(x﹣![]() )2﹣
)2﹣![]() =0.
=0.
故选D.
【点评】本题主要考查了配方法在解一元二次方程中的应用,ax2+bx+c=a(x2+![]() x+
x+![]() ﹣
﹣![]() )+c=a(x+
)+c=a(x+![]() )2﹣
)2﹣![]() +c=a(x+
+c=a(x+![]() )2+
)2+![]() .
.
7.(2分)关于x的方程[mx2﹣(m﹣n)x﹣n](x2﹣6x+12)=0(其中m、n是实数,且m≠0)共有()个不等实根.
A.2 B.3 C.4 D.1或2
【分析】解方程得x2﹣6x+12=0或mx2﹣(m﹣n)x﹣n=0,再结合两个方程的根的判别式的符号即可得出结论.
【解答】解:若要[mx2﹣(m﹣n)x﹣n](x2﹣6x+12)=0,则需x2﹣6x+12=0或mx2﹣(m﹣n)x﹣n=0.
在方程x2﹣6x+12=0中,
△=b2﹣4ac=36﹣4×12=﹣12<0,
∴x2﹣6x+12=0无实数根;
在方程mx2﹣(m﹣n)x﹣n=0中,
∵m≠0,
∴△=b2﹣4ac=[﹣(m﹣n)]2﹣4m×(﹣n)=(m+n)2≥0,
∴方程mx2﹣(m﹣n)x﹣n=0有一个或两个实数根.
综上可知:关于x的方程[mx2﹣(m﹣n)x﹣n](x2﹣6x+12)=0(其中m、n是实数,且m≠0)共有一个或两个实数根.
故选D.
【点评】本题考查了根的判别式,解题的关键是根据根的判别式的符号确定根的个数.本题属于基础题,难度不大,解决该题型题目时,由根的判别式的符号确定根的个数是关键.
8.(2分)某市快乐公园有一长方形的花园,长为400米,宽为300米,现准备在其四周铺设一条等宽的休闲小路,所增加的面积为花园面积的![]() ,则此休闲小路的宽是()
,则此休闲小路的宽是()
A.4米 B.5米 C.8米 D.10米
【分析】设此休闲小路的宽是x米.根据增加的面积为花园面积的![]() ,列出方程即可解决问题;
,列出方程即可解决问题;
【解答】解:设此休闲小路的宽是x米.
由题意(400+2x)(300+2x)﹣400×300=![]() ×400×300,
×400×300,
解得x=10或﹣360(舍弃),
所以此休闲小路的宽是10米.
故选D.
【点评】本题考查一元二次方程的应用,解题的关键是学会设未知数,寻找等量关系,列出方程解决问题.
9.(2分)已知k≠1,一元二次方程(k﹣1)x2+kx+1=0有根,则k的取值范围是()
A.k≠2 B.k>2
C.k<2且k≠1 D.k为一切不是1的实数
【分析】一元二次方程若有根,则△=b2﹣4ac≥0,建立关于k的不等式,求得k的取值范围.
【解答】解:∵a=k﹣1,b=k,c=1
∴△=b2﹣4ac=k2﹣4×(k﹣1)×1≥0,
整理得:△=(k﹣2)2≥0,
又∵k≠1,
∴k为一切不等于1的实数.
故选D.
【点评】总结:一元二次方程根的情况与判别式△的关系:
(1)△>0⇔方程有两个不相等的实数根;
(2)△=0⇔方程有两个相等的实数根;
(3)△<0⇔方程没有实数根.
10.(2分)对于一元二次方程ax2+bx+c=0(a≠0),有下列说法:
①当a<0,且b>a+c时,方程一定有实数根;
②若ac<0,则方程有两个不相等的实数根;
③若a﹣b+c=0,则方程一定有一个根为﹣1;
④若方程有两个不相等的实数根,则方程bx2+ax+c=0一定有两个不相等的实数根.
其中正确的有()
A.①②③ B.①②④ C.②③ D.①②③④
【分析】利用根的判别式△=b2﹣4ac,结合字母的取值,逐一探讨得出答案即可.
【解答】解:①由a<0,且b>a+c,得出(a+c)2<b2,△=b2﹣4ac=(a+c)2﹣4ac=(a﹣c)2≥0,关于x的方程ax2+bx+c=0必有实根;故①正确;
②若ac<0,a、c异号,则△=b2﹣4ac>0,方程ax2+bx+c=0一定有实数根,所以②正确;
③若a﹣b+c=0,b=a+c,△=b2﹣4ac=(a+c)2﹣4ac=(a﹣c)2≥0,则一元二次方程ax2+bx+c=0有两个实数根,所以③错误;
④若方程ax2+bx+c=0有两个不相等的实数根,c可能为0,则方程bx2+ax+c=0,a2﹣4bc>0一定有两个不相等的实数根,所以④正确.
故选:B.
【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2﹣4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.
二、填空题:((每小题3分,共24分)
11.(3分)关于x的方程(a2﹣1)x2+2(a﹣1)x+2a+2=0,当a =﹣1 时,为一元一次方程.当a ≠±1 时,为一元二次方程.
【分析】根据只有一个未知数且未知数最高次数为1的整式方程叫做一元一次方程,只有一个未知数且未知数最高次数为2的整式方程叫做一元二次方程,可得答案.
【解答】解:关于x的方程(a2﹣1)x2+2(a﹣1)x+2a+2=0,当a=﹣1时,为一元一次方程.当a≠±1时,为一元二次方程,
故答案为:a=﹣1,a≠±1.
【点评】本题考查了一元二次方程,只有一个未知数且未知数最高次数为2的整式方程叫做一元二次方程,一般形式是ax2+bx+c=0(且a≠0).特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.
12.(3分)已知x=1是一元二次方程x2+mx+n=0的一个根,则m2+2mn+n2的值为 1 .
【分析】首先把x=1代入一元二次方程x2+mx+n=0中得到m+n+1=0,然后把m2+2mn+n2利用完全平方公式分解因式即可求出结果.
【解答】解:∵x=1是一元二次方程x2+mx+n=0的一个根,
∴m+n+1=0,
∴m+n=﹣1,
∴m2+2mn+n2=(m+n)2=(﹣1)2=1.
故答案为:1.
【点评】此题主要考查了方程的解的定义,利用方程的解和完全平方公式即可解决问题.
13.(3分)已知关于x的一元二次方程2x2﹣x﹣k=0有两个相等的实数根,则k的值为 ﹣![]() .
.
【分析】由方程根的个数,结合根的判别式即可得出关于k的一元一次方程,解方程即可得出结论.
【解答】解:∵关于x的一元二次方程2x2﹣x﹣k=0有两个相等的实数根,
∴△=(﹣1)2﹣4×2×(﹣k)=1+8k=0,
解得:k=﹣![]() .
.
故答案为:﹣![]() .
.
【点评】本题考查了根的判别式以及解一元一次方程,解题的关键是找出关于k的一元一次方程.本题属于基础题,难度不大,解决该题型题目时,根据根的个数结合根的判别式得出方程(不等式或不等式组)是关键.
14.(3分)若![]() ,则以x,y的值为两边长的等腰三角形的周长是 10 .
,则以x,y的值为两边长的等腰三角形的周长是 10 .
【分析】先根据非负数的性质列式求出x、y的值,再分4是腰长与底边两种情况讨论求解.
【解答】解:根据题意得,x﹣2=0,y﹣4=0,
解得x=2,y=4,
①2是腰长时,三角形的三边分别为2、2、4,
∵2+2=4,
∴不能组成三角形,
②2是底边时,三角形的三边分别为2、4、4,
能组成三角形,周长=2+4+4=10,
所以,三角形的周长为10.
故答案为:10
【点评】本题考查了等腰三角形的性质,绝对值非负数,算术平方根非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0求出x、y的值是解题的关键,难点在于要分情况讨论并且利用三角形的三边关系进行判断.
15.(3分)实数a、b满足(a+b)2+a+b﹣2=0,则(a+b)2的值为 4或1 .
【分析】本题可将(a+b)看成一个整体,不妨设为x,则原式可变形为:x2+x﹣2=0,即可解出a+b的值,由此可计算(a+b)2的值.
【解答】解:设x=a+b,则原方程可化为:
x2+x﹣2=0
∴x=﹣2或x=1,
∴(a+b)2的值为4或1,
故答案为4或1.
【点评】本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的提点灵活选用合适的方法,本题运用的是换元法,旨在教会学生使用换元法把复杂的题目简单化.
16.(3分)若关于x的方程x2﹣(m+5)|x|+4=m恰有3个实数解,则实数m= 4 .
【分析】把方程看作关于|x|的一元二次方程,则它有一个0根和一个正实数根,所以4﹣m=0.
【解答】解:|x|2﹣(m+5)|x|+4﹣m=0,
关于|x|的方程有一个0根和一个正实数根,
所以4﹣m=0,
解得m=4.
故答案为4.
【点评】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2﹣4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.
17.(3分)根据题意列一元二次方程:有10个边长均为x的正方形,它们的面积之和是200,则有 10x2=200 .
【分析】根据正方形的面积公式及10个正方形面积之和可列方程;
【解答】解:设边长均为x,根据题意得:10x2=200,
故答案为:10x2=200;
【点评】本题主要考查根据实际问题列一元二次方程的能力,掌握正方形面积公式是根本.
18.(3分)如果25x2﹣(k﹣1)xy+9y2是一个完全平方式,那么K的值为 31或﹣29 .
【分析】根据完全平方公式,即可解答.
【解答】解:∵25x2﹣(k﹣1)xy+9y2是一个完全平方式,
∴﹣(k﹣1)xy=±2•5x•3y
∴﹣(k﹣1)xy=±30xy,
∴﹣(k﹣1)=±30,
∴k=31或﹣29.
故答案为:31或﹣29.
【点评】本题考查了完全平方公式,解决本题的关键是熟记完全平方公式.
三.解一元二次方程(每小题24分,共24分)
19.(24分)(1)x2=64
(2)5x2﹣![]() =0
=0
(3)(x+5)2=16
(4)8(3﹣x)2﹣72=0
(5)2y=3y2
(6)2(2x﹣1)﹣x(1﹣2x)=0
(7)3x(x+2)=5(x+2)
(8)(1﹣3y)2+2(3y﹣1)=0.
【分析】(1)利用直接开平方法求解即可;
(2)先求出x2,再利用直接开平方法求解即可;
(3)把(x+5)看作一个整体,利用直接开平方法求解即可;
(4)把(3﹣x)看作一个整体,利用直接开平方法求解即可;
(5)利用因式分解法求解即可;
(6)提取公因式(2x﹣1),利用因式分解法求解即可;
(7)利用因式分解法求解即可;
(8)利用因式分解法求解即可.
【解答】解:(1)∵(±8)2=64,
∴x=±8,
即x1=8,x2=﹣8;
(2)移项得,5x2=![]() ,
,
系数化为1得,x2=![]() ,
,
x=±![]() ,
,
即x1=![]() ,x2=﹣
,x2=﹣![]() ;
;
(3)x+5=±4,
x1=﹣1,x2=﹣9;
(4)移项,系数化为1得,(3﹣x)2=9,
3﹣x=±3,
即x1=6,x2=0;
(5)移项得,3y2﹣2y=0,
y(3y﹣2)=0,
∴y=0,3y﹣2=0,
解得y1=0,y2=![]() ;
;
(6)(2x﹣1)(2+x)=0,
∴2x﹣1=0,2+x=0,
解得x1=![]() ,x2=﹣2;
,x2=﹣2;
(7)移项得,3x(x+2)﹣5(x+2)=0,
(x+2)(3x﹣5)=0,
∴x+2=0,3x﹣5=0,
解得x1=﹣2,x2=![]() ;
;
(8)(3y﹣1)(3y﹣1+2)=0,
∴3y﹣1=0,3y+1=0,
解得y1=![]() ,y2=﹣
,y2=﹣![]() .
.
【点评】本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.
四.解方程解应用题(共32分,20----22题每题6分,23---24题每题7分)
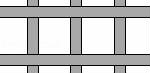
20.(6分)如图,有一块长为30米,宽为10米的长方形菜地,在菜地里要留出南北三条,东西两条,宽度一样的小路,并使实际种植面积为216平方米,求小路的宽应为几米.
【分析】本题中草坪的总面积=矩形场地的面积﹣五条道路的面积和+五条道路中重叠的两个小正方形的面积,据此可得出关于道路宽度的方程,求出道路的宽度.
【解答】解:设小路的宽为x米,则(30﹣3x)(10﹣2x)=216,
整理得,x2﹣15x+14=0,解得:x1=1,x2=14,
∵x2=14超过矩形的边长,
∴x2=14不合题意,
符合题意的是x=1.
答:小路的宽为1m.
【点评】本题考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
21.(6分)某商店将进价为16元的商品按每件20元售出,每天可售出300件,现在采取提高商品售价减少销售量的办法增加利润.若这种商品每件的销售价每提高1元其销售量就减少20件,问每件售价定为多少元时,才能使每天利润为1680元,且销售量较少?
【分析】设售价为x元,则有(x﹣进价)[每天售出的数量﹣(x﹣20)×20]=每天利润,解方程求解即可.
【解答】方法一解:设每件售价为x元,根据题意列方程得(x﹣16)[300﹣(x﹣20)×20]=1680,
整理得:x2﹣51x+644=0,
解得x1=23,x2=28.
因为要销售量较少,故将x1=23舍去.
答:每件售价28元.
方法二解:设每件售价提高了x元,根据题意列方程得(x+4)(300﹣20x)=1680,
整理得:x2﹣11x+24=0,
解得x1=3,x2=8.
因为要销售量较少,故将x1=3舍去.当x2=8时,x+20=28(元)
答:每件售价28元.
【点评】本题考查的是一元二次方程的应用.读懂题意,找到等量关系准确的列出方程是解题的关键.
22.(6分)有一间长18米,宽7.5米的会议室,在它的中间铺一块地毯,地毯的面积是会议室面积的一半,且四周未铺地毯外的宽度相同,求四周所留的宽度是多少米?
【分析】等量关系为:地毯的长×地毯的宽=会议室面积的一半,设出未知数,列出方程解答即可.
【解答】解:设留的宽度为x米.
(18﹣2x)(7.5﹣2x)=![]() ×18×7.5,
×18×7.5,
解得x1=11.25(不合题意,舍去),x2=1.5.
∴x=1.5.
答:留的宽度为1.5米.
【点评】考查一元二次方程的应用;得到地毯的边长是解决本题的易错点;得到地毯面积的等量关系是解决本题的关键.
23.(7分)一件上衣,每件原价500元,第一次降价后,销售甚慢,于是再次进行大幅降价,第二次降价的百分率是第一次降价的百分率的2倍,结果这批上衣以每件240元的价格迅速售出,求两次降价的百分率各是多少.
【分析】先设第次降价的百分率是x,则第一次降价后的价格为500(1﹣x)元,第二次降价后的价格为500(1﹣2x),根据两次降价后的价格是240元建立方程,求出其解即可;
【解答】解:设第一次降价的百分率为x,则第二次降价的百分率为2x,根据题意得:
500(1﹣x)(1﹣2x)=240,
解得x1=0.2=20%,x2=1.3=130%.
则第一次降价的百分率为20%,第二次降价的百分率为40%.
【点评】本题考查了一元二次方程解实际问题,读懂题意,找出题目中的等量关系,列出方程,求出符合题的解即可.
24.(7分)汽车租赁公司共有出租车120辆,每辆汽车的日租金为160元,出租业务供不应求,为适合市场需求,经有关部门批准,公司准备适当提高日租金,经市场调查发现,一辆汽车的日租金每增加10元,每天出租的汽车相应的减少6辆,若不考虑其他因素,一辆汽车的日租金提高几个10元时,才能使公司的日租金收入最高?公司的日租金总收入比提高租金前增加了多少?(公司日租金总收入=每辆汽车的日租金×公司每天出租的汽车数)
【分析】由题意我们可知:日租金的总额=每辆汽车的日租金×出租车的数量,然后根据这个关系即可得出函数关系式,再配方求出二次函数的最值.
【解答】解:设该公司的每辆汽车日租金提高x个10元,日租金总收入为y,则
y=(160+10x)(120﹣6x)=﹣60(x﹣2)2+19440,
当x=2时,ymax=19440,
即一辆汽车的日租金提高2个10元时,才能使公司的日租金收入最高.
19440﹣120×160
=19440﹣19200
=240(元).
故一辆汽车的日租金提高2个10元时,才能使公司的日租金收入最高,公司的日租金总收入比提高租金前增加了240元.
【点评】本题考查了二次函数的应用,属于基础题,关键是用配方法求二次函数的最值.