请选择
2017年广东省汕尾市城区中考数学一模试卷(解析版含答案)
由于版式的问题,试题可能会出现乱码的现象,为了方便您的阅读请点击全屏查看一、选择题(本大题共10小题,每小题3分,满分30分)
1.﹣5的绝对值是()
A.![]() B.﹣5 C.5 D.﹣
B.﹣5 C.5 D.﹣![]()
2.下列图形不是轴对称图形的是()
A.![]() B.
B.![]() C.
C. D.
D.![]()
3.据报道,2016年10月17日7时30分28秒,神舟十一号载人飞船在酒泉发射升空,与天宫二号在距离地面393000米的太空轨道进行交会对接,而这也是未来我国空间站运行的轨道高度393000用科学记数法表示为()
A.0.393×106 B.3.93×105 C.0.393×105 D.39.3×104
4.下列计算正确的是()
A.x2•x3=x6 B.(x2)3=x5 C.x2+x3=x5 D.x6÷x3=x3
5.三角形的外心到三角形三个顶点的距离相等,它是三角形()
A.三个内角平分线的交点 B.三边垂直平分线的交点
C.三条高线的交点 D.三条中线的交点
6.小华班上比赛投篮,每人投6球,如图是班上所有学生投进球数的饼图.根据图,下列关于班上所有学生投进球数的统计量,何者正确?()
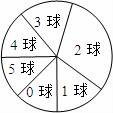
A.中位数为3 B.中位数为2.5 C.众数为5 D.众数为2
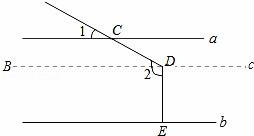
7.如图,直线a∥b,射线DC与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,则∠2的度数为()
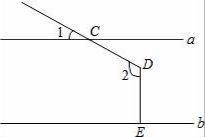
A.115° B.125° C.155° D.165°
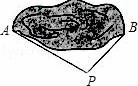
8.为估计池塘两岸A、B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么AB间的距离不可能是()
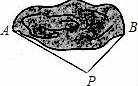
A.5m B.15m C.20m D.28m
9.一个多边形的内角和是1260°,这个多边形的边数是()
A.6 B.7 C.8 D.9
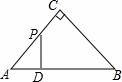
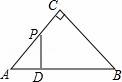
10.如图,△ABC是等腰直角三角形,AC=BC,AB=4,D为AB上的动点,DP⊥AB交折线A﹣C﹣B于点P,设AD=x,△ADP的面积为y,则y与x的函数图象正确的是()
A.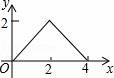 B.
B.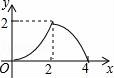
C.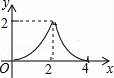 D.
D.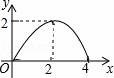
二、填空题(本大题6小题,每小题4分,共24分)
11.在﹣3,2,![]() 这三个实数中,绝对值最大的是:.
这三个实数中,绝对值最大的是:.
12.分解因式:2b2﹣8b+8=.
13.函数y=![]() 中,自变量x的取值范围是.
中,自变量x的取值范围是.
14.计算:![]() =.
=.
15.用同样大小的黑色棋子按如图所示的规律摆放,则第239个图共有枚棋子.

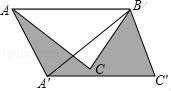
16.如图,在△ABC中,AB=6cm,∠CAB=45°,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为.
三、解答题(一)(本大题3小题,每小题6分,共18分)
17.(6分)解不等式组:![]() ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
![]()
18.(6分)先化简,再求值:(![]() +1)÷
+1)÷![]() ,其中a=
,其中a=![]() ﹣1.
﹣1.
19.(6分)“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
请结合图表完成下列各题:
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |
(1)表中a的值为;
(2)频数分布直方图补充完整;
(3)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
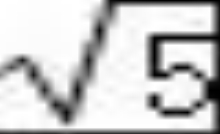
四、解答题(二)(本大题3小题,每小题7分,共21分)
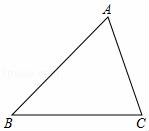
20.(7分)如图,已知△ABC.
(1)请用尺规作△ABC的中位线DE,其中点D、E分别在AB、AC上.
(尺规作图,保留作图痕迹,不写作法)
(2)延长DE至点F,使得EF=DE,求证:四边形DBCF是平行四边形.
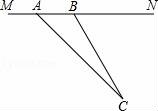
21.(7分)目前,崇明县正在积极创建全国县级文明城市,交通部门一再提醒司机:为了安全,请勿超速,并在进一步完善各类监测系统,如图,在陈海公路某直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.
(参考数据:![]() ,
,![]() )
)
22.(7分)已知关于x的一元二次方程(x﹣3)(x﹣4)=|a|.
(1)求证:对于任意实数a,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求a的值及方程的另一个根.
五、解答题(三)(本大题3小题,每小题9分,共27分)
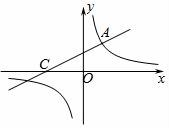
23.(9分)如图,直线y=![]() x+2与双曲线相交于点A(m,3),与x轴交于点C.
x+2与双曲线相交于点A(m,3),与x轴交于点C.
(1)求双曲线解析式;
(2)根据图象直接写出,在什么范围时,一次函数的值小于反比例函数的值;
(3)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
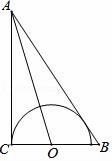
24.(9分)如图,在Rt△ABC中,∠ACB=90°,∠BAC的角平分线交BC于点O,OC=2,以点O为圆心OC为半径作圆.
(1)求证:AB为⊙O的切线;
(2)如果tan∠BAO=![]() ,求cosB的值.
,求cosB的值.
25.(9分)如图,抛物线y=ax2+bx与x轴相交于点A(8,0),且经过原点.顶点M在第四象限,过点M作MB⊥x轴,且BM=4,点P(a,0)是线段OA上一动点,连结PM,将线段PM绕点P逆时针旋转90°得到线段PC,过点C作y轴的平行线交x轴于点N,交抛物线于点D,连结BC和MD.
(1)求抛物线的解析式;
(2)求点C的坐标(用含a的代数式表示);
(3)当以点M、B、C、D为顶点的四边形是平行四边形时,求点P的坐标.

2017年广东省汕尾市城区中考数学一模试卷参考答案与试题解析
一、选择题(本大题共10小题,每小题3分,满分30分)
1.﹣5的绝对值是()
A.![]() B.﹣5 C.5 D.﹣
B.﹣5 C.5 D.﹣![]()
【考点】15:绝对值.
【分析】根据一个负数的绝对值是它的相反数求解即可.
【解答】解:﹣5的绝对值是5.
故选C.
【点评】本题考查了绝对值的定义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
2.下列图形不是轴对称图形的是()
A.![]() B.
B.![]() C.
C. D.
D.![]()
【考点】P3:轴对称图形.
【分析】根据轴对称图形的概念求解.如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴.
【解答】解:A、是轴对称图形,故选项错误;
B、不是轴对称图形,故选项正确;
C、是轴对称图形,故选项错误;
D、是轴对称图形,故选项错误.
故选:B.
【点评】此题主要考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
3.据报道,2016年10月17日7时30分28秒,神舟十一号载人飞船在酒泉发射升空,与天宫二号在距离地面393000米的太空轨道进行交会对接,而这也是未来我国空间站运行的轨道高度393000用科学记数法表示为()
A.0.393×106 B.3.93×105 C.0.393×105 D.39.3×104
【考点】1I:科学记数法—表示较大的数.
【分析】用科学记数法表示较大的数时,一般形式为a×10﹣n,其中1≤|a|<10,n为整数,据此判断即可.
【解答】解:393000=3.93×105.
故选:B.
【点评】此题主要考查了用科学记数法表示较大的数,一般形式为a×10﹣n,其中1≤|a|<10,确定a与n的值是解题的关键.
4.下列计算正确的是()
A.x2•x3=x6 B.(x2)3=x5 C.x2+x3=x5 D.x6÷x3=x3
【考点】48:同底数幂的除法;35:合并同类项;46:同底数幂的乘法;47:幂的乘方与积的乘方.
【分析】根据同底数幂的乘法、幂的乘方,合并同类项,同底数幂的除法求出每个式子的值,再进行判断即可.
【解答】解:A、x2•x3=x5,故本选项错误;
B、(x2)3=x6,故本选项错误;
C、x2和x3不是同类项,不能合并,故本选项错误;
D、x6÷x3=x3,故本选项正确;
故选D.
【点评】本题考查了同底数幂的乘法、幂的乘方,合并同类项,同底数幂的除法的应用,主要考查学生的计算能力和辨析能力.
5.三角形的外心到三角形三个顶点的距离相等,它是三角形()
A.三个内角平分线的交点 B.三边垂直平分线的交点
C.三条高线的交点 D.三条中线的交点
【考点】MA:三角形的外接圆与外心.
【分析】根据线段垂直平分线上的点到线段两端点的距离相等解答即可.
【解答】解:由线段垂直平分线的性质可知,线段垂直平分线上的点到线段两端点的距离相等,
则三角形的外心到三角形三个顶点的距离相等,它是三角形三边垂直平分线的交点,
故选:B.
【点评】本题考查的是三角形的外接圆和外心的概念和性质,掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键.
6.小华班上比赛投篮,每人投6球,如图是班上所有学生投进球数的饼图.根据图,下列关于班上所有学生投进球数的统计量,何者正确?()
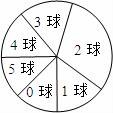
A.中位数为3 B.中位数为2.5 C.众数为5 D.众数为2
【考点】VB:扇形统计图;W4:中位数;W5:众数.
【分析】根据中位数和众数的定义,结合扇形统计图,选出正确选项即可.
【解答】解:由图可知:班内同学投进2球的人数最多,故众数为2;
因为不知道每部分的具体人数,所以无法判断中位数.
故选D.
【点评】本题考查了扇形统计图的知识,通过图形观察出投进2球的人数最多是解题的关键.
7.如图,直线a∥b,射线DC与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,则∠2的度数为()
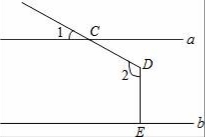
A.115° B.125° C.155° D.165°
【考点】JA:平行线的性质.
【分析】如图,过点D作c∥a.由平行线的性质进行解题.
【解答】解:如图,过点D作c∥a.
则∠1=∠CDB=25°.
又a∥b,DE⊥b,
∴b∥c,DE⊥c,
∴∠2=∠CDB+90°=115°.
故选:A.
【点评】本题考查了平行线的性质.此题利用了“两直线平行,同位角相等”来解题的.
8.为估计池塘两岸A、B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么AB间的距离不可能是()
A.5m B.15m C.20m D.28m
【考点】K6:三角形三边关系.
【分析】首先根据三角形的三边关系定理求出AB的取值范围,然后再判断各选项是否正确.
【解答】解:∵PA、PB、AB能构成三角形,
∴PA﹣PB<AB<PA+PB,即4m<AB<28m.
故选D.
【点评】已知三角形的两边,则第三边的范围是:大于已知的两边的差,而小于两边的和.
9.一个多边形的内角和是1260°,这个多边形的边数是()
A.6 B.7 C.8 D.9
【考点】L3:多边形内角与外角.
【分析】设边数为n,由多边形内角和公式可列方程,可求得边数.
【解答】解:
设这个多边形的边数为n,
由题意可得:(n﹣2)×180°=1260°,
解得n=9,
∴这个多边形的边数为9,
故选D.
【点评】本题主要考查多边形的内角和,掌握多边形的内角和公式是解题的关键,即多边形的内角和=(n﹣2)180°.
10.如图,△ABC是等腰直角三角形,AC=BC,AB=4,D为AB上的动点,DP⊥AB交折线A﹣C﹣B于点P,设AD=x,△ADP的面积为y,则y与x的函数图象正确的是()
A.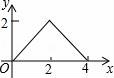 B.
B.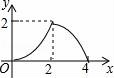 C.
C. D.
D.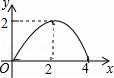
【考点】E7:动点问题的函数图象.
【分析】根据题意可以列出y与x的函数解析式,从而可以确定y与x的函数图象,从而可以得到正确的选项,本题得以解决.
【解答】解:由题意可得,
当0≤x≤2时,y=![]() ,
,
当2≤x≤4时,y=![]() =
=![]() ,
,
∴当0≤x≤2时,函数图象为y=![]() 的右半部分,当2≤x≤4时,函数图象为y=
的右半部分,当2≤x≤4时,函数图象为y=![]() 的右半部分,
的右半部分,
故选B.
【点评】本题考查动点问题的函数图象,解题的关键是明确题意,可以列出相应的函数解析式、确定函数的图象.
二、填空题(本大题6小题,每小题4分,共24分)
11.在﹣3,2,![]() 这三个实数中,绝对值最大的是: ﹣3 .
这三个实数中,绝对值最大的是: ﹣3 .
【考点】2A:实数大小比较.
【分析】首先求出每个数的绝对值各是多少;然后根据实数大小比较的方法,判断出在﹣3,2,![]() 这三个实数中,绝对值最大的是哪个即可.
这三个实数中,绝对值最大的是哪个即可.
【解答】解:|﹣3|=3,|2|=2,|![]() |=
|=![]() ,
,
∵3>2>![]() ,
,
∴在﹣3,2,![]() 这三个实数中,绝对值最大的是﹣3.
这三个实数中,绝对值最大的是﹣3.
故答案为:﹣3.
【点评】此题主要考查了绝对值的含义和求法,以及实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:正实数>0>负实数,两个负实数绝对值大的反而小.
12.分解因式:2b2﹣8b+8= 2(b﹣2)2 .
【考点】55:提公因式法与公式法的综合运用.
【分析】先提取公因式2,再根据完全平方公式进行二次分解.完全平方公式:a2﹣2ab+b2=(a﹣b)2.
【解答】解:原式=2(b2﹣4b+4)
=2(b﹣2)2.
故答案为:2(b﹣2)2.
【点评】本题考查了提公因式法,公式法分解因式,提取公因式后利用完全平方公式进行二次分解,注意分解要彻底.
13.函数y=![]() 中,自变量x的取值范围是 x≥﹣2且x≠0 .
中,自变量x的取值范围是 x≥﹣2且x≠0 .
【考点】E4:函数自变量的取值范围.
【分析】根据被开方数大于等于0,分母不等于0列式计算即可得解.
【解答】解:由题意得,x+2≥0且x≠0,
解得x≥﹣2且x≠0.
故答案为:x≥﹣2且x≠0.
【点评】本题考查了函数自变量的范围,一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.
14.计算:![]() = 1 .
= 1 .
【考点】2C:实数的运算;6E:零指数幂;6F:负整数指数幂;T5:特殊角的三角函数值.
【分析】本题涉及零指数幂、负指数幂、特殊角的三角函数值、绝对值等四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
【解答】解:原式=1+![]() ﹣2×
﹣2×![]() ﹣(2﹣
﹣(2﹣![]() )
)
=1+2﹣![]() ﹣2+
﹣2+![]()
=1,
故答案为:1.
【点评】本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负零指数幂、负指数幂、特殊角的三角函数值、绝对值等考点的运算.
15.用同样大小的黑色棋子按如图所示的规律摆放,则第239个图共有 718 枚棋子.

【考点】38:规律型:图形的变化类.
【分析】根据图形中点的个数得到有关棋子个数的通项公式,然后代入数值计算即可.
【解答】解:观察图形知:
第1个图形有3+1=4个棋子,
第2个图形有3×2+1=7个棋子,
第3个图形有3×3+1=10个棋子,
第4个图形有3×4+1=13个棋子,
…
第n个图形有3n+1个棋子,
当n=239时,3×239+1=718个,
故答案为:718.
【点评】本题考查了图形的变化类问题,能够根据图形得到通项公式是解决本题的关键.
16.如图,在△ABC中,AB=6cm,∠CAB=45°,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为 9![]() cm2 .
cm2 .
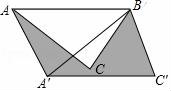
【考点】R2:旋转的性质;KW:等腰直角三角形.
【分析】根据旋转的性质得∠ABA′=45°,BA′=BA,△ABC≌△A′BC′,则S△ABC=S△A′BC′,再利用面积的和差可得S阴影部分=S△ABA′,接着证明△ADB为等腰直角三角形,得到∠ADB=90°,进而得到AD的长,然后利用三角形面积公式计算S△ABA,从而得到S阴影部分.
【解答】解:如图所示,设AC与BA′相交于D,
∵△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,
∴∠ABA′=45°,BA′=BA=6,△ABC≌△A′BC′,
∴S△ABC=S△A′BC′
∵S四边形AA′C′B=S△ABC+S阴影部分=S△A′BC′+S△ABA′
∴S阴影部分=S△ABA′
∵∠BAC=45°,
∴△ADB为等腰直角三角形,
∴∠ADB=90°,AD=![]() AB=3
AB=3![]() ,
,
∴S△ABA′=![]() AD•BA′=
AD•BA′=![]() ×3
×3![]() ×6=9
×6=9![]() ,
,
∴阴影部分的面积=9![]() cm2.
cm2.
故答案为:9![]() cm2.
cm2.
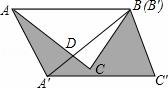
【点评】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的性质.运用面积的和差解决不规则图形的面积是解决此题的关键.
三、解答题(一)(本大题3小题,每小题6分,共18分)
17.解不等式组:![]() ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
![]()
【考点】CB:解一元一次不等式组;C4:在数轴上表示不等式的解集.
【分析】首先把两条不等式的解集分别解出来,再根据大大取大,小小取小,比大的小比小的大取中间,比大的大比小的小无解的原则,把不等式的解集用一个式子表示出来.
【解答】解:由(1)得4x>4,
∴x>1;
由(2)得2x+2﹣6<x,
∴x<4
∴原不等式组的解集为1<x<4.
![]()
【点评】本题考查不等式组的解法和在数轴上的表示法,如果是表示大于或小于号的点要用空心,如果是表示大于等于或小于等于号的点用实心.
18.先化简,再求值:(![]() +1)÷
+1)÷![]() ,其中a=
,其中a=![]() ﹣1.
﹣1.
【考点】6D:分式的化简求值.
【分析】先将原分式化简,然后将a的值代入即可求出答案.
【解答】解:当a=![]() ﹣1时,
﹣1时,
∴原式=[![]() +1]•
+1]•![]()
=![]() +
+![]()
=![]()
=![]()
=![]()
=![]()
=![]()
【点评】本题考查分式的化简求值,解题的关键是熟练运用分式的运算法则,本题属于基础题型
19.“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
请结合图表完成下列各题:
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |
(1)表中a的值为 12 ;
(2)频数分布直方图补充完整;
(3)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
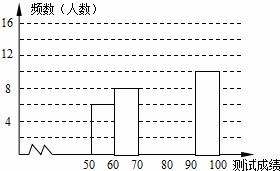
【考点】V8:频数(率)分布直方图;V7:频数(率)分布表.
【分析】(1)根据题意和表中的数据可以求得a的值;
(2)由表格中的数据可以将频数分布表补充完整;
(3)根据表格中的数据和测试成绩不低于80分为优秀,可以求得优秀率;
【解答】解:(1)由题意和表格,可得
a=50﹣6﹣8﹣14﹣10=12,
故答案为:12;
(2)补充完整的频数分布直方图如下图所示:
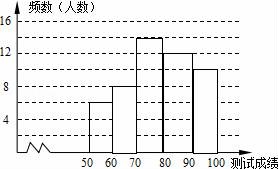
(2)∵测试成绩不低于80分为优秀,
∴本次测试的优秀率是:![]() ×100%=44%.
×100%=44%.
【点评】本题考查了频数分布表、频数分布直方图,解题的关键是明确题意,找出所求问题需要的条件,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
四、解答题(二)(本大题3小题,每小题7分,共21分)
20.如图,已知△ABC.
(1)请用尺规作△ABC的中位线DE,其中点D、E分别在AB、AC上.
(尺规作图,保留作图痕迹,不写作法)
(2)延长DE至点F,使得EF=DE,求证:四边形DBCF是平行四边形.
【考点】N3:作图—复杂作图;KX:三角形中位线定理;L6:平行四边形的判定.
【分析】(1)分别作AB、AC的中垂线找到AB、AC的中点,连接中点即可得;
(2)证明BC∥DF且BC=DF即可.
【解答】解:(1)如图,线段DE即为所求;
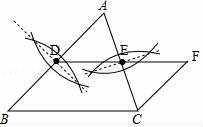
(2)∵DE是△ABC的中位线,
∴BC=2DE,且BC∥DE,
∵EF=DE,
∴DF=2DE,
∴BC=DF,
∴四边形DBCF是平行四边形.
【点评】本题主要考查作图﹣复杂作图及三角形的中位线定理、平行四边形的判定,熟练掌握中垂线的作图和中位线定理是解题的关键.
21.目前,崇明县正在积极创建全国县级文明城市,交通部门一再提醒司机:为了安全,请勿超速,并在进一步完善各类监测系统,如图,在陈海公路某直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.
(参考数据:![]() ,
,![]() )
)
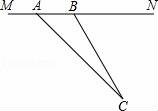
【考点】T8:解直角三角形的应用.
【分析】根据题意结合锐角三角函数关系得出BH,CH,AB的长进而求出汽车的速度,进而得出答案.
【解答】解:此车没有超速.理由如下:
过C作CH⊥MN,垂足为H,
∵∠CBN=60°,BC=200米,
∴CH=BC•sin60°=200×![]() =100
=100![]() (米),
(米),
BH=BC•cos60°=100(米),
∵∠CAN=45°,
∴AH=CH=100![]() 米,
米,
∴AB=100![]() ﹣100≈73(m),
﹣100≈73(m),
∴车速为![]() m/s.
m/s.
∵60千米/小时=![]() m/s,
m/s,
又∵14.6<![]() ,
,
∴此车没有超速.
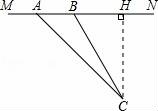
【点评】此题主要考查了勾股定理以及锐角三角函数关系的应用,得出AB的长是解题关键.
22.已知关于x的一元二次方程(x﹣3)(x﹣4)=|a|.
(1)求证:对于任意实数a,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求a的值及方程的另一个根.
【考点】AB:根与系数的关系;AA:根的判别式.
【分析】(1)将原方程整理成一般式,再结合根的判别式即可得出△=4|a|+1>0,由此即可证出结论;
(2)将x=1代入一元二次方程中即可求出a值,设方程的另一个根为m,根据根与系数的关系即可得出1+m=7,解之即可得出方程的另一个根.
【解答】(1)证明:原方程整理后可得:x2﹣7x+12﹣|a|=0,
∴△=(﹣7)2﹣4×(12﹣|a|)=4|a|+1>0,
∴对于任意实数a,方程总有两个不相等的实数根;
(2)解:将x=1代入x2﹣7x+12﹣|a|=0中,
1﹣7+12﹣|a|=0,解得:a=±6.
设方程的另一个根为m,
则有1+m=7,
解得:m=6.
∴a的值为±6,方程的另一个根为6.
【点评】本题考查了根与系数的关系、一元二次方程的解以及根的判别式,解题的关键是:(1)熟练掌握“当△>0时,方程有两个不相等的实数根”;(2)将x=1代入原方程求出a值.
五、解答题(三)(本大题3小题,每小题9分,共27分)
23.如图,直线y=![]() x+2与双曲线相交于点A(m,3),与x轴交于点C.
x+2与双曲线相交于点A(m,3),与x轴交于点C.
(1)求双曲线解析式;
(2)根据图象直接写出,在什么范围时,一次函数的值小于反比例函数的值;
(3)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
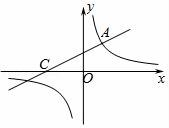
【考点】G8:反比例函数与一次函数的交点问题.
【分析】(1)把A坐标代入直线解析式求出m的值,确定出A坐标,即可确定出双曲线解析式;
(2)联立一次函数与反比例函数解析式求出交点坐标,利用图象确定出一次函数值小于反比例函数值时x的范围即可.
(3)设P(x,0),表示出PC的长,高为A纵坐标,根据三角形ACP面积求出x的值,确定出P坐标即可.
【解答】解:(1)把A(m,3)代入直线解析式得:3=![]() m+2,即m=2,
m+2,即m=2,
∴A(2,3),
把A坐标代入y=![]() ,得k=6,
,得k=6,
则双曲线解析式为y=![]() ;
;
(2)联立一次函数与反比例函数解析式得,
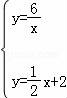 ,
,
解得:![]() 或
或![]() ,
,
∴一次函数的值小于反比例函数的值时x的范围是:x<﹣6或x>2;
(3)对于直线y=![]() x+2,令y=0,得到x=﹣4,即C(﹣4,0),
x+2,令y=0,得到x=﹣4,即C(﹣4,0),
设P(x,0),可得PC=|x+4|,
∵△ACP面积为3,
∴![]() |x+4|•3=3,即|x+4|=2,
|x+4|•3=3,即|x+4|=2,
解得:x=﹣2或x=﹣6,
则P坐标为(﹣2,0)或(﹣6,0).
【点评】此题考查了反比例函数与一次函数的交点问题,涉及的知识有:待定系数法确定函数解析式,坐标与图形性质,以及三角形面积求法,熟练掌握待定系数法是解本题的关键.
24.如图,在Rt△ABC中,∠ACB=90°,∠BAC的角平分线交BC于点O,OC=2,以点O为圆心OC为半径作圆.
(1)求证:AB为⊙O的切线;
(2)如果tan∠BAO=![]() ,求cosB的值.
,求cosB的值.

【考点】MD:切线的判定;T7:解直角三角形.
【分析】(1)如图作OM⊥AB于M,根据角平分线性质定理,可以证明OM=OC,由此即可证明.
(2)设BM=x,OB=y,列方程组即可解决问题.
【解答】解:(1)如图,作OM⊥AB于M,
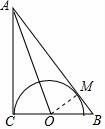
∵OA平分∠CAB,OC⊥AC,OM⊥AB,
∴OC=OM,
∴AB是⊙O的切线,
(2)设BM=x,OB=y,则y2﹣x2=22①,
∵cosB=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴x2+6x=y2+2y ②,
由①②可以得到:y=3x﹣2,
∴(3x﹣2)2﹣x2=4,
∴x=![]() ,y=
,y=![]() ,
,
∴cosB=![]() =
=![]() .
.
【点评】本题考查切线的判定、勾股定理、三角函数等知识,解题的关键是记住圆心到直线的距离等于半径,这条直线就是圆的切线,学会设未知数列方程组解决问题.
25.如图,抛物线y=ax2+bx与x轴相交于点A(8,0),且经过原点.顶点M在第四象限,过点M作MB⊥x轴,且BM=4,点P(a,0)是线段OA上一动点,连结PM,将线段PM绕点P逆时针旋转90°得到线段PC,过点C作y轴的平行线交x轴于点N,交抛物线于点D,连结BC和MD.
(1)求抛物线的解析式;
(2)求点C的坐标(用含a的代数式表示);
(3)当以点M、B、C、D为顶点的四边形是平行四边形时,求点P的坐标.

【考点】HF:二次函数综合题.
【分析】(1)根据题意先求得M的坐标,然后根据待定系数法即可求得抛物线的解析式;
(2)通过三角形全等求得PB=CN,BM=PN,分类讨论P在B点的左边与右边,从而求得C的坐标;
(3)分类讨论点P在OB上时、OE上时,把C的横坐标代入抛物线的解析式求得D的坐标,然后根据平行四边形的对边相等列出等式,解这个方程即可求得a的值,进而求得P的坐标.
【解答】解:(1)∵点A与点O关于MB对称,
∴抛物线的对称轴为x=4.
又∵MB=4,
∴M(4,﹣4).
将点A和点M的坐标代入抛物线的解析式得:![]() ,
,
解得:a=![]() ,b=﹣2.
,b=﹣2.
∴抛物线的解析式为:y=![]() x2﹣2x.
x2﹣2x.
(2)∵∠MPB+∠BPC=90°,∠MPB+∠PMB=90°,
∴∠CPB=∠PMB.
在△MPB和△PCN中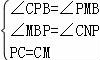
∴△MPB≌△PCN.
∴PB=CN,PN=BM=4
∵P(a,0),OP=a,且点P是线段OE上的动点
∴PB=CN=|4﹣a|,ON=|a+4|
①如图1,当点P在点B左边时,点C在x轴上方,
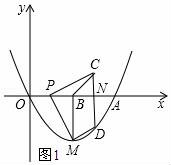
a<4,4﹣a>0,PB=CN=4﹣a,
∴C(a+4,4﹣a)
②如图2,当点P在点B右边时,点C在x轴下方,
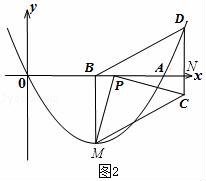
a>4,4﹣a<0,
∴PB=|4﹣a|=﹣(4﹣a)=a﹣4
∴CN=a﹣4
∴C(a+4,4﹣a)
综上所述,点C坐标是C(a+4,4﹣a)
(3)如图1所示,当点P在OB上时,
由(2)可知点C的坐标为(a+4,4﹣a).
∵四边形BMDC为平行四边形,
∴CD=BM=4.
将x=a+4代入抛物线的解析式得:y=![]() (a+4)2﹣2(a+4)=
(a+4)2﹣2(a+4)=![]() a2﹣4.
a2﹣4.
∴CD=4﹣a﹣(![]() a2﹣4)=4,解得:a=﹣2+2
a2﹣4)=4,解得:a=﹣2+2![]() 或a=﹣2﹣2
或a=﹣2﹣2![]() (舍去).
(舍去).
∴点P的坐标为(﹣2+2![]() ,0).
,0).
如图2所示:当点P在线段BA上时.点C的坐标为(a+4,4﹣a),则点D的坐标为(a+4,![]() a2﹣4)
a2﹣4)
∴CD=![]() a2﹣4﹣(4﹣a)=4.
a2﹣4﹣(4﹣a)=4.
解得:a=﹣2+2![]() 或a=﹣2﹣2
或a=﹣2﹣2![]() (舍去).
(舍去).
∴点P的坐标为(﹣2+2![]() ,0).
,0).
综上所述,点P的坐标为(﹣2+2![]() ,0)或(﹣2+2,0).
,0)或(﹣2+2,0).
【点评】本题着重考查了待定系数法求二次函数解析式、图形旋转变换、三角形全等的判定和性质、平行四边形的性质、函数图象的交点的求法,找出图形中的全等三角形,利用全等三角形的性质得到相关线段的长度是解答问题(2)的关键,依据平行四边形的对边相等列出关于a的方程是解题的关键.