请选择
2017—2018河源黄冈实验中学九年级上学期数学月考试题(word版含答案)
由于版式的问题,试题可能会出现乱码的现象,为了方便您的阅读请点击全屏查看
全卷满分 120 分,考试时间 100分钟
一、选择题(本大题10小题,每题3分,共30分)
1.下列方程是一元二次方程的是()
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2.下列说法:①四边相等的四边形一定是菱形。②顺次连接矩形各边中点形成的四边形一定是正方形。③对角线相等的四边形一定是矩形。④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分
其中正确的有()个.
A.4B.3C.2D.1
3. 一个不透明的布袋里装有10个红球,4个白球,6个黄球,它们除颜色外其余都相同,从袋中任意摸出1个球,是黄球的概率为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.以下一元二次方程的两根之和为2的是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 5. 如图,某小区计划在一块长为
5. 如图,某小区计划在一块长为![]() ,宽为
,宽为![]() 的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为
的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为![]() .若设道路的宽为
.若设道路的宽为![]() ,则下面所列方程正确的是( )
,则下面所列方程正确的是( )
A.![]() B.
B.![]()
C. ![]() D.
D.![]()
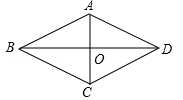 6.求证:菱形的两条对角线互相垂直.
6.求证:菱形的两条对角线互相垂直.
已知:如图,四边形ABCD是菱形,对角线AC,BD交于点O.求证:AC⊥BD.以下是排乱的证明过程:
①又BO=DO;②∴AO⊥BD,即AC⊥BD;③∵四边形ABCD是菱形;④∴AB=AD.
证明步骤正确的顺序是()
A.③→②→①→④ B.③→④→①→②C.①→②→④→③ D.①→④→③→②
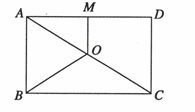 7. 如图,点
7. 如图,点![]() 是矩形
是矩形![]() 的对角线
的对角线![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() 的长为()
的长为()
A. 5 B. 4 C. ![]() D.
D.![]()
8.一元二次方程![]() 的根的情况是()
的根的情况是()
A.有两个相等的实数根B.有两个不相等的实数根 C. 无法确定D.没有实数根
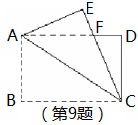 9.如图,矩形纸片
9.如图,矩形纸片![]() ABCD中,A
ABCD中,A![]() B=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )
B=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() [来源:学
[来源:学
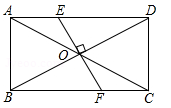 10.如图,矩形ABCD的对
10.如图,矩形ABCD的对![]() 角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=
角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=![]() ,∠AEO=120°,则FC的长度为()
,∠AEO=120°,则FC的长度为()
A.1B.2C.![]() D.
D.![]() 。
。
二、填空题(每题4分,共24分)
11. 一个箱子装有除颜色外都相同的2个白球,2个黄球,1个红球.现添加同种型号的1个球,使得从中随机抽取1个球,这三种颜色的球被抽到的概率都是![]() ,那么添加的球是.
,那么添加的球是.
12.观察表格,一元二次方程![]() 最精确的一个近似解是 (精确到0.1).
最精确的一个近似解是 (精确到0.1).
x | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 |
| -0.71 | -0.54 | -0.35 | -0.14 | 0.09 | 0.34 | 0.61 |
13.已知关于![]() 的一元二次方程
的一元二次方程![]() 有实数根,则
有实数根,则![]() 的取值范围是 .
的取值范围是 .
14.某加工厂九月份加工了10吨干果,十一月份加工了13吨干果.设该厂加工干果重量的月平均增长率为x,根据题意可列方程为.
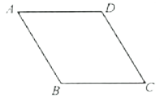 15. 如图,在菱形
15. 如图,在菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是这个菱形内部或边上的一点,若以
是这个菱形内部或边上的一点,若以![]() 为顶点的三角形是等腰三角形,则
为顶点的三角形是等腰三角形,则![]() ,
,![]() (
(![]() ,
,![]() 两点不重合)两点间的最短距离为 cm.
两点不重合)两点间的最短距离为 cm.
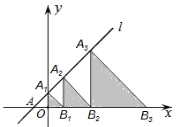 16. 如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2,A3,…在直线l上,点B1,B2,B3,…在x轴的正半轴上,若△A1OB1,△A2B1B2,△A3B2B3,…,依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形AnBn﹣1Bn顶点Bn的横坐标为 .
16. 如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2,A3,…在直线l上,点B1,B2,B3,…在x轴的正半轴上,若△A1OB1,△A2B1B2,△A3B2B3,…,依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形AnBn﹣1Bn顶点Bn的横坐标为 .
三、解答题(一)(本大题3小题,每题6分,共18分)
17.用适当的方法解一元二次方程(6分)
(1)(x-1)(x+2)=2x+4 (2)![]() (3)
(3)![]()
18. 十一放假期间,陶光辉老师和赵峥老师准备到云南的大理(记为A)、丽江(记为B)、香格里拉(记为C)、束河古镇(记为D)的一个景点去游玩,他们各自在这四个景点中任选一个,每个景点都被选中的可能性相同.
(1)陶光辉老师选择去香格里拉旅游的概率为 .(2分)
(2)用树状图或列表的方法求陶光辉老师和赵峥老师都选择去丽江旅游的概率(4分)
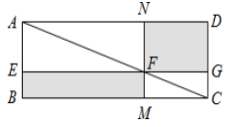 19.数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.,
19.数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.,
请根据上图完成这个推论的证明过程.
证明:![]() ,
,![]() (____________+____________).
(____________+____________).
易知,![]() ,_____________=______________,______________=_____________.
,_____________=______________,______________=_____________.
可得![]() .
.
四、解答题(二)(本大题3小题,每题7分,共21分)
20、已知关于x的方程x2+(2k﹣1)x+k2﹣1=0有两个实数根x1,x2.
 (1)求实数k的取值范围;(3分)(2)若x1,x2满足x12+x22=16+x1x2,求实数k的值.(4分)
(1)求实数k的取值范围;(3分)(2)若x1,x2满足x12+x22=16+x1x2,求实数k的值.(4分)
21、如图,在四边形![]() 中,
中,![]() 为一条对角线,
为一条对角线,![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(1)求证:四边形![]() 为菱形;(3分)(2)连接
为菱形;(3分)(2)连接![]() ,若
,若![]() 平分
平分![]() ,求
,求![]() 的长.(4分)
的长.(4分)
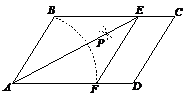 22、如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于
22、如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(1)根据以上尺规作图的过程,求证四边形ABEF是菱形;(3分)
(2)若菱形ABEF的周长为16,AE=4![]() ,求∠C的大小.(4分)
,求∠C的大小.(4分)
五、解答题(三)(本大题3小题,每题9分,共27分)
23、翔丰商场销售某种冰箱,每台进价为2500元,当销售价为2900元时,每天能售出8台,为了迎接“双11”活动,商场决定采取适当降价的方式促销,经调查发现,如果销售价每降低50元,那么商场每天就可以多售出4台。
(1)降价前商场每月销售该商品的利润是多少元?(4分)
(2)要使商场每天销售这种冰箱的利润达到5000元,则每件商品应降价多少元?(5分)
 24、如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
24、如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;(3分)
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3分)
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形。(3分)
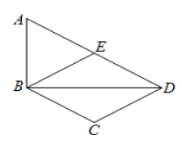
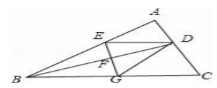 25、如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
25、如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;(4分)
(2)若∠ABC=30°,∠C=45°,ED=2![]() ,点H是BD上的一个动点,求HG+HC的最小值.(5分)
,点H是BD上的一个动点,求HG+HC的最小值.(5分)