请选择
由于格式问题此试题可能会出现乱码的情况
为了方便您阅读请点击右上角的全屏查看
2018秦皇岛市中考数学冲刺试题
一、选择题
1.若二次根式![]() 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( )
A.x≥2 B.x>2 C.x<2 D.x≤2
2.下列各组数中,不能作为直角三角形边长的是( )
A.9,12,15 B.5,12,13 C.1,2,![]() D.,3,5,7
D.,3,5,7
3.如图,若∠1=∠2,AD=BC,则四边形ABCD是( )
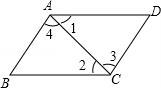
A.平行四边形 B.菱形
C.正方形 D.以上说法都不对
4.若一次函数y=kx+b的图象经过y轴的正半轴上一点,且y随x的增大而减小,那么k,b的取值范围是( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
5.(秦皇岛中考数学)对于一组数据:3、3、2、3、6、3、10、3、6、3、2,下列说法正确的是( )
A.这组数据的众数是3
B.这组数据的众数与中位数的数值不等
C.这组数据的中位数与平均数的数值相等
D.这组数据的平均数与众数的数值相等
6.某校七年级有13名同学参加百米竞赛,预赛成绩各不相同,要取前6名参加决赛,小梅已经知道了自己的成绩,她想知道自己能否进入决赛,还需要知道这13名同学成绩的( )
A.中位数 B.众数 C.平均数 D.极差
7.已知数据x1,x2,…,xn的方差是S21,x1﹣a,x2﹣a,…,xn﹣a的方差是S22,则( )
A.S21>S22 B.S21>S22
C.S21=S22 D.S21与S21无法比较
8.一次函数y=x图象向下平移2个单位长度后,对应函数关系式是( )
A.y=2x B.y=x C.y=x+2 D.y=x﹣2
9.一次函数y=kx+b,经过(1,1),(2,﹣4),则k与b的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知△ABC的周长为50cm,中位线DE=8cm,中位线EF=10cm,则另一条中位线DF的长是( )
A.5cm B.7cm C.9cm D.10cm
11.已知x+y=![]() ,xy=
,xy=![]() ,则x2+y2的值为( )
,则x2+y2的值为( )
A.5 B.3 C.2 D.1
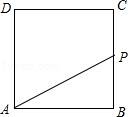
12.如图,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A 的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是( )
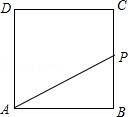
A.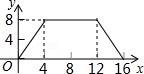 B.
B.
C.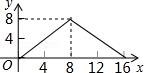 D.
D.
二、填空题
13.2014![]() 2015= .
2015= .
14(秦皇岛中考数学).数据3,1,﹣2,5,3的平均数是 ,中位数是 ,众数是 .
15.某中学期中考试,八(1)班第一小组10人数学考试的成绩为:100分3人,90分5人,80分2人,则全组数学平均成绩为 分.
16.在函数![]() 中,自变量x的取值范围是 .
中,自变量x的取值范围是 .
17.已知直线y=2x+8与x轴和y轴的交点的坐标分别是 、 ;与两条坐标轴围成的三角形的面积是 .
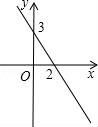
18.如图,直线y=kx+b(k≠0)与x轴的交点为(2,0),与y轴的交点为(0,3),则关于x的不等式0<kx+b<3的解集是 .
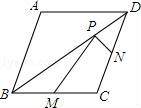
19.已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值= .
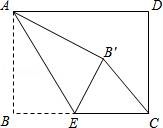
20.如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为 .
三、解答题
21.(秦皇岛中考数学)为了从甲、乙两名同学中选拔一个参加比赛,对他们的射击水平进行了测验,两个在相同条件下各射靶10次,命中的环数如下(单位:环)
甲:7,8,6,8,6,5,9,10,7,4
乙:9,5,7,8,6,8,7,6,7,7
(1)求![]() 甲,
甲,![]() 乙,S甲2,S乙2;
乙,S甲2,S乙2;
(2)你认为该选拔哪名同学参加射击比赛?为什么?
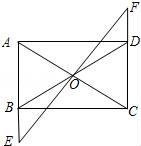
22.如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB,CD的延长线分别交于E,F.
(1)求证:△BOE≌△DOF;
(2)当EF与AC满足什么关系时,以A,E,C,F为顶点的四边形是菱形?证明你的结论.
23.已知:如图,直线y1=x+1经过点B(2,n),且与x轴交于点A.
(1)求n及点A坐标;
(2)若函数y2=kx(k≠0)的图象经过点B,请画出这个函数的图象,并结合图象比较函数y1与y2的大小关系.

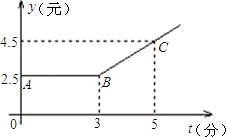
24.如图,折线ABC是甲地向乙地打长途电话所需要付的电话费y(元)与通话时间t(分钟)之间关系的图象(注意:通话时间不足1分钟按1分钟计费).
(1)通话1分钟,要付电话费多少元?通话5分钟要付多少电话费?
(2)通话多少分钟内,所支付的电话费一样多?
(3)通话3.2分钟应付电话费多少元?
25.(秦皇岛中考数学)抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库.已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A、B两库的路程和运费如下表:(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
| 路程(千米) | 运费(元/吨•千米) | ||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
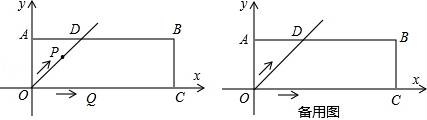
26.在平面直角坐标系xOy中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒![]() 个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.
个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.
(1)当点P移动到点D时,t= 秒;
(2)连接点A,C,求直线AC的解析式;
(3)若点M是直线AC上第一象限内一点,是否存在某一时刻,使得四边形OPMQ为平行四边形?若存在,请直接写出t的值及点M的坐标;若不存在,请说明理由.
2015-2016学年河北省秦皇岛市八年级(下)期末数学试卷
参考答案与试题解析
一、选择题
1.(秦皇岛中考数学)若二次根式![]() 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( )
A.x≥2 B.x>2 C.x<2 D.x≤2
【考点】二次根式有意义的条件.
【分析】由二次根式![]() 在实数范围内有意义,可得2﹣x≥0,继而求得答案.
在实数范围内有意义,可得2﹣x≥0,继而求得答案.
【解答】解:∵二次根式![]() 在实数范围内有意义,
在实数范围内有意义,
∴2﹣x≥0,
解得:x≤2.
故选D.
【点评】此题考查了二次根式有意义的条件.注意二次根式中的被开方数必须是非负数,否则二次根式无意义.
2.下列各组数中,不能作为直角三角形边长的是( )
A.9,12,15 B.5,12,13 C.1,2,![]() D.,3,5,7
D.,3,5,7
【考点】勾股定理的逆定理.
【分析】根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形.如果没有这种关系,这个就不是直角三角形.
【解答】解:A、92+122=152,符合勾股定理的逆定理,故本选项不符合题意;
B、52+122=132,符合勾股定理的逆定理,故本选项不符合题意;
C、12+(![]() )2=22,符合勾股定理的逆定理,故本选项不符合题意;
)2=22,符合勾股定理的逆定理,故本选项不符合题意;
D、32+52≠72,不符合勾股定理的逆定理,故本选项符合题意.
故选D.
【点评】本题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.
3.如图,若∠1=∠2,AD=BC,则四边形ABCD是( )

A.平行四边形 B.菱形
C.正方形 D.以上说法都不对
【考点】平行四边形的判定.
【分析】根据题意判断出△ACD≌△CAB,故可得出∠3=∠4,由此可得出结论.
【解答】解:在△ACD与△CAB中,
∵ ,
,
∴△ACD≌△CAB,
∴∠3=∠4,
∴AB∥CD,
∴四边形ABCD是平行四边形.
故选A.
【点评】本题考查的是平行四边形的判定,熟知两组对边分别平行的四边形是平行四边形是解答此题的关键.
4.(秦皇岛中考数学)若一次函数y=kx+b的图象经过y轴的正半轴上一点,且y随x的增大而减小,那么k,b的取值范围是( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
【考点】一次函数图象与系数的关系.
【分析】根据图象在坐标平面内的位置关系确定k,b的取值范围,从而求解.
【解答】解:函数值y随x的增大而减小,则k<0;
图象与y轴的正半轴相交,则b>0.
故选C.
【点评】函数值y随x的增大而减小⇔k<0;函数值y随x的增大而增大⇔k>0;
一次函数y=kx+b图象与y轴的正半轴相交⇔b>0,一次函数y=kx+b图象与y轴的负半轴相交⇔b<0,一次函数y=kx+b图象过原点⇔b=0.
5.对于一组数据:3、3、2、3、6、3、10、3、6、3、2,下列说法正确的是( )
A.这组数据的众数是3
B.这组数据的众数与中位数的数值不等
C.这组数据的中位数与平均数的数值相等
D.这组数据的平均数与众数的数值相等
【考点】众数;加权平均数;中位数.
【分析】根据平均数、众数、中位数的定义和公式分别对每一项进行分析,再进行判断即可.
【解答】解:数据3出现次数最多,故众数为3,
故选A.
【点评】此题考查了平均数、众数、中位数的知识,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,众数是一组数据中出现次数最多的数.
6.某校七年级有13名同学参加百米竞赛,预赛成绩各不相同,要取前6名参加决赛,小梅已经知道了自己的成绩,她想知道自己能否进入决赛,还需要知道这13名同学成绩的( )
A.中位数 B.众数 C.平均数 D.极差
【考点】统计量的选择.
【分析】由于有13名同学参加百米竞赛,要取前6名参加决赛,故应考虑中位数的大小.
【解答】解:共有13名学生参加竞赛,取前6名,所以小梅需要知道自己的成绩是否进入前六.
我们把所有同学的成绩按大小顺序排列,第7名学生的成绩是这组数据的中位数,
所以小梅知道这组数据的中位数,才能知道自己是否进入决赛.
故选:A.
【点评】本题考查了用中位数的意义解决实际问题.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
7.(秦皇岛中考数学)已知数据x1,x2,…,xn的方差是S21,x1﹣a,x2﹣a,…,xn﹣a的方差是S22,则( )
A.S21>S22 B.S21>S22
C.S21=S22 D.S21与S21无法比较
【考点】方差.
【分析】列出二个算式的方差表达式进行对比即可.
【解答】解:由题意知,设原来的数据的平均数为![]() 1,每个数据都减小了a,则平均数变为
1,每个数据都减小了a,则平均数变为![]() 1﹣a,原来的方差s12=
1﹣a,原来的方差s12=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2],现在的方差s22=
)2],现在的方差s22=![]() [(x1+a﹣
[(x1+a﹣![]() ﹣a)2+(x2+a﹣
﹣a)2+(x2+a﹣![]() ﹣a)2+…+(xn+a﹣
﹣a)2+…+(xn+a﹣![]() ﹣a)2]=
﹣a)2]=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2],即方差不变.
)2],即方差不变.
故选C.
【点评】本题说明了当一组数据的每一个数都加上(或减去)同一个数a后,得到的新数据的方差不变.
8.一次函数y=x图象向下平移2个单位长度后,对应函数关系式是( )
A.y=2x B.y=x C.y=x+2 D.y=x﹣2
【考点】一次函数图象与几何变换.
【分析】注意平移时k的值不变,只有b发生变化.
【解答】解:原直线的k=1,b=0;向下平移2个单位长度得到了新直线,
那么新直线的k=1,b=0﹣2=﹣2.
∴新直线的解析式为y=x﹣2.
故选D.
【点评】本题考查了一次函数图象的几何变换,难度不大,要注意平移后k值不变.
9.(秦皇岛中考数学)一次函数y=kx+b,经过(1,1),(2,﹣4),则k与b的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【考点】待定系数法求一次函数解析式.
【分析】由于一次函数y=kx+b经过(1,1),(2,﹣4),应用待定系数法即可求出函数的解析式.
【解答】解:把(1,1),(2,﹣4)代入一次函数y=kx+b,
得![]() ,
,
解得:![]() .
.
故选:C.
【点评】本题考查用待定系数法求解函数解析式,只需把所给的点的坐标代入即可.
10.已知△ABC的周长为50cm,中位线DE=8cm,中位线EF=10cm,则另一条中位线DF的长是( )
A.5cm B.7cm C.9cm D.10cm
【考点】三角形中位线定理;平行四边形的判定.
【分析】三角形的中位线等于第三边的一半,所以三条中位线的长为:50÷2=25,所求的中位线为25减去另两条中位线的长.
【解答】解:另一条中位线DF的长为:50÷2﹣(8+10)=7,故选B.
【点评】本题利用了三角形的中位线等于第三边的一半求解.
11.已知x+y=![]() ,xy=
,xy=![]() ,则x2+y2的值为( )
,则x2+y2的值为( )
A.5 B.3 C.2 D.1
【考点】二次根式的化简求值.
【分析】由(x+y)2=x2+y2+2xy,得出x2+y2=(x+y)2﹣2xy,再带入已知数据求解即可.
【解答】解:x2+y2=(x+y)2﹣2xy
=(![]() )2﹣2
)2﹣2![]()
=3+2+2![]() ﹣2
﹣2![]()
=5.
故选A.
【点评】本题考查了二次根式的化简求值,解答本题的关键在于先对原式进行恰当的化简然后代入求值.
12(秦皇岛中考数学).如图,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A 的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是( )
A. B.
B.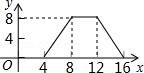 C.
C.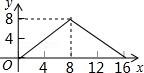 D.
D.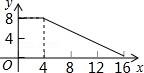
【考点】动点问题的函数图象.
【分析】根据动点从点A出发,首先向点D运动,此时y不随x的增加而增大,当点P在DC山运动时,y随着x的增大而增大,当点P在CB上运动时,y不变,据此作出选择即可.
【解答】解:①当点P由点A向点D运动时,y的值为0;
②当点P在DC上运动时,y随着x的增大而增大;
③当点p在CB上运动时,y=ABAD,y不变;
④当点P在BA上运动时,y随x的增大而减小.
故选B.
【点评】本题考查了动点问题的函数图象,解决动点问题的函数图象问题关键是发现y随x的变化而变化的趋势.
二、填空题
13.(1﹣![]() )2014
)2014![]() 2015= 1+
2015= 1+![]() .
.
【考点】二次根式的混合运算.
【分析】把(1+![]() )2015化成(1+
)2015化成(1+![]() )2014(1+
)2014(1+![]() ),与(1﹣
),与(1﹣![]() )2014,利用积的乘方的逆用得:[(1﹣
)2014,利用积的乘方的逆用得:[(1﹣![]() )(1+
)(1+![]() )]2014=(﹣1)2014=1,最后得出结果.
)]2014=(﹣1)2014=1,最后得出结果.
【解答】解:(1﹣![]() )2014
)2014![]() 2015,
2015,
=(1﹣![]() )2014
)2014![]() 2014(1+
2014(1+![]() ),
),
=[(1﹣![]() )(1+
)(1+![]() )]2014(1+
)]2014(1+![]() ),
),
=1+![]() .
.
【点评】本题考查了二次根式的混合运算,主要运用了积的乘方的逆用,对高次方进行变形,化成1或﹣1的高次方进行计算,从而得出结果.
14.(秦皇岛中考数学)数据3,1,﹣2,5,3的平均数是 2 ,中位数是 3 ,众数是 3 .
【考点】众数;算术平均数;中位数.
【分析】先根据平均数=![]() 求出该组数据的平均数,再将该组数据按照从小到大的顺序排列,根据中位数和众数的概念解答即可.
求出该组数据的平均数,再将该组数据按照从小到大的顺序排列,根据中位数和众数的概念解答即可.
【解答】解:平均数=![]() =
=![]() =2,
=2,
将这组数据按照从小到大的顺序排列为:﹣2,1,3,3,5,
可得出中位数为:3,众数为:3.
故答案为:2,3,3.
【点评】本题考查了众数和中位数的概念:(1)一组数据中出现次数最多的数据叫做众数.(2)将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
15.某中学期中考试,八(1)班第一小组10人数学考试的成绩为:100分3人,90分5人,80分2人,则全组数学平均成绩为 91 分.
【考点】加权平均数.
【分析】首先求出这10人的数学总成绩为多少;然后求出全组数学平均成绩为多少即可.
【解答】解:(100×3+90×5+80×2)÷10
=(300+450+160)÷10
=910÷10
=91(分)
答:全组数学平均成绩为91分.
故答案为:91.
【点评】此题主要考查了平均数的含义和求法,要熟练掌握.
16.在函数![]() 中,自变量x的取值范围是 x≤1且x≠﹣2 .
中,自变量x的取值范围是 x≤1且x≠﹣2 .
【考点】函数自变量的取值范围;分式有意义的条件;二次根式有意义的条件.
【分析】根据二次根式的性质和分式的意义,被开方数大于等于0,分母不等于0,就可以求解.
【解答】解:根据二次根式有意义,分式有意义得:1﹣x≥0且x+2≠0,
解得:x≤1且x≠﹣2.
故答案为:x≤1且x≠﹣2.
【点评】本题考查的知识点为:分式有意义,分母不为0;二次根式的被开方数是非负数.
17.(秦皇岛中考数学)已知直线y=2x+8与x轴和y轴的交点的坐标分别是 (﹣4,0) 、 (0,8) ;与两条坐标轴围成的三角形的面积是 16 .
【考点】一次函数图象上点的坐标特征.
【分析】让直线解析式的纵坐标为0即可得到与x轴的交点坐标;让横坐标为0即可得到与y轴的交点坐标,与两条坐标轴围成的三角形的面积应等于![]() ×x轴上点的横坐标的绝对值×y轴上点的纵坐标.
×x轴上点的横坐标的绝对值×y轴上点的纵坐标.
【解答】解:当y=0时,x=﹣4,
∴直线y=2x+8与x轴的交点坐标为(﹣4,0);
当x=0时,y=8,
∴直线y=2x+8与y轴的交点坐标为(0,8);
∴三角形的底是|﹣4|,高是8,
∴与两条坐标轴围成的三角形的面积是![]() ×|﹣4|×8=16.
×|﹣4|×8=16.
故填(﹣4,0)、(0,8)、16.
【点评】本题考查的知识点为:一次函数与y轴的交点的横坐标为0;一次函数与x轴的交点的纵坐标为0,在求面积的时候注意坐标与线段的转化.
18.如图,直线y=kx+b(k≠0)与x轴的交点为(2,0),与y轴的交点为(0,3),则关于x的不等式0<kx+b<3的解集是 0<x<2 .

【考点】一次函数与一元一次不等式.
【分析】根据一次函数的性质得出y随x的增大而增大,当x<2时,y<0,即可求出答案.
【解答】解:∵直线y=kx+b(k>0)与x轴的交点为(2,0),与y轴的交点为(0,3),
∴y随x的增大而增大,
当x<2时,y<0,
即kx+b<0.
0<kx+b<3的解集为:0<x<2,
故答案为:0<x<2
【点评】本题主要考查对一次函数与一元一次不等式,一次函数的性质等知识点的理解和掌握,能熟练地运用性质进行说理是解此题的关键.
19.已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值= 5 .

【考点】轴对称-最短路线问题;菱形的性质.
【分析】作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,求出CP、PB,根据勾股定理求出BC长,证出MP+NP=QN=BC,即可得出答案.
【解答】(秦皇岛中考数学)解: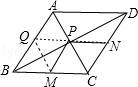
作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,
∵四边形ABCD是菱形,
∴AC⊥BD,∠QBP=∠MBP,
即Q在AB上,
∵MQ⊥BD,
∴AC∥MQ,
∵M为BC中点,
∴Q为AB中点,
∵N为CD中点,四边形ABCD是菱形,
∴BQ∥CD,BQ=CN,
∴四边形BQNC是平行四边形,
∴NQ=BC,
∵四边形ABCD是菱形,
∴CP=![]() AC=3,BP=
AC=3,BP=![]() BD=4,
BD=4,
在Rt△BPC中,由勾股定理得:BC=5,
即NQ=5,
∴MP+NP=QP+NP=QN=5,
故答案为:5.
【点评】本题考查了轴对称﹣最短路线问题,平行四边形的性质和判定,菱形的性质,勾股定理的应用,解此题的关键是能根据轴对称找出P的位置.
20.如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为 3或6 .
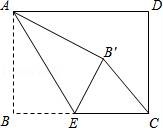
【考点】翻折变换(折叠问题).
【分析】当△CEB′为直角三角形时,有两种情况:
①当点B′落在矩形内部时,如答图1所示.
连结AC,先利用勾股定理计算出AC=10,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=6,可计算出CB′=4,设BE=x,则EB′=x,CE=8﹣x,然后在Rt△CEB′中运用勾股定理可计算出x.
②当点B′落在AD边上时,如答图2所示.此时四边形ABEB′为正方形.
【解答】(秦皇岛中考数学)解:当△CEB′为直角三角形时,有两种情况:
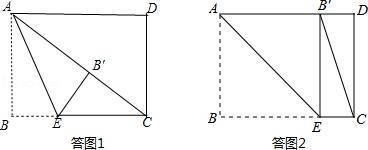
①当点B′落在矩形内部时,如答图1所示.
连结AC,
在Rt△ABC中,AB=6,BC=8,
∴AC=![]() =10,
=10,
∵∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,只能得到∠EB′C=90°,
∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,如图,
∴EB=EB′,AB=AB′=6,
∴CB′=10﹣6=4,
设BE=x,则EB′=x,CE=8﹣x,
在Rt△CEB′中,
∵EB′2+CB′2=CE2,
∴x2+42=(8﹣x)2,
解得x=3,
∴BE=3;
②当点B′落在AD边上时,如答图2所示.
此时ABEB′为正方形,
∴BE=AB=6.
综上所述,BE的长为3或6.
故答案为:3或6.
【点评】本题考查了折叠问题:折叠前后两图形全等,即对应线段相等;对应角相等.也考查了矩形的性质以及勾股定理.注意本题有两种情况,需要分类讨论,避免漏解.
三、(秦皇岛中考数学)解答题
21.为了从甲、乙两名同学中选拔一个参加比赛,对他们的射击水平进行了测验,两个在相同条件下各射靶10次,命中的环数如下(单位:环)
甲:7,8,6,8,6,5,9,10,7,4
乙:9,5,7,8,6,8,7,6,7,7
(1)求![]() 甲,
甲,![]() 乙,S甲2,S乙2;
乙,S甲2,S乙2;
(2)你认为该选拔哪名同学参加射击比赛?为什么?
【考点】方差.
【分析】(1)根据平均数的计算公式先求出平均数,再根据方差公式进行计算即可;
(2)根据方差的意义,方差越小越稳定,即可得出答案.
【解答】解:(1)![]() 甲=(7+8+6+8+6+5+9+10+7+4)÷10=7;
甲=(7+8+6+8+6+5+9+10+7+4)÷10=7;
![]() 乙=(9+5+7+8+6+8+7+6+7+7)÷10=7;
乙=(9+5+7+8+6+8+7+6+7+7)÷10=7;
S甲2=![]() [2(7﹣7)2+2(8﹣7)2+2(6﹣7)2+(5﹣7)2+(9﹣7)2+(10﹣7)2+(4﹣7)2]=3;
[2(7﹣7)2+2(8﹣7)2+2(6﹣7)2+(5﹣7)2+(9﹣7)2+(10﹣7)2+(4﹣7)2]=3;
S乙2=![]() [4(7﹣7)2+2(8﹣7)2+2(6﹣7)2+(5﹣7)2+(9﹣7)2]=1.2;
[4(7﹣7)2+2(8﹣7)2+2(6﹣7)2+(5﹣7)2+(9﹣7)2]=1.2;
(2)∵![]() 甲=
甲=![]() 乙,S甲2>S乙2,
乙,S甲2>S乙2,
∴乙较稳定,
∴该选拔乙同学参加射击比赛.
【点评】本题考查方差的定义:一般地设n个数据,x1,x2,…xn的平均数为![]() ,则方差S2=
,则方差S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
22.如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB,CD的延长线分别交于E,F.
(1)求证:△BOE≌△DOF;
(2)当EF与AC满足什么关系时,以A,E,C,F为顶点的四边形是菱形?证明你的结论.

【考点】菱形的判定;全等三角形的判定;矩形的性质.
【分析】(秦皇岛中考数学)(1)由矩形的性质:OB=OD,AE∥CF证得△BOE≌△DOF;
(2)若四边形EBFD是菱形,则对角线互相垂直,因而可添加条件:EF⊥AC,
当EF⊥AC时,∠EOA=∠FOC=90°,
∵AE∥FC,
∴∠EAO=∠FCO,矩形对角线的交点为O,
∴OA=OC,
∴△AOE≌△COF,
∴OE=OF,根据对角线互相垂直平分的四边形是菱形.
∴四边形EBFD是菱形.
【解答】(1)证明:∵四边形ABCD是矩形,
∴OB=OD(矩形的对角线互相平分),
AE∥CF(矩形的对边平行).
∴∠E=∠F,∠OBE=∠ODF.
∴△BOE≌△DOF(AAS).
(2)解:当EF⊥AC时,四边形AECF是菱形.
证明:∵四边形ABCD是矩形,
∴OA=OC(矩形的对角线互相平分).
又∵由(1)△BOE≌△DOF得,OE=OF,
∴四边形AECF是平行四边形(对角线互相平分的四边形是平行四边形)
又∵EF⊥AC,
∴四边形AECF是菱形(对角线互相垂直的平行四边形是菱形).
【点评】本题利用了:1、矩形的性质,2、全等三角形的判定和性质,3、菱形的判定.
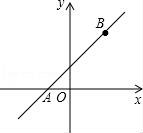
23.已知:如图,直线y1=x+1经过点B(2,n),且与x轴交于点A.
(1)求n及点A坐标;
(2)若函数y2=kx(k≠0)的图象经过点B,请画出这个函数的图象,并结合图象比较函数y1与y2的大小关系.
【考点】一次函数图象上点的坐标特征;正比例函数的图象.
【分析】(1)把B点代入y1=x+1可求得n的值,可求得函数解析式,再令y=0,可求得A点坐标;
(2)把B点坐标代入y2=kx可求得k的值,可求得解析式,利用两点法可画出其图象,再结合图象可比较y1与y2的大小关系.
【解答】(秦皇岛中考数学)解:
(1)把点B坐标代入y1=x+1中,可得n=2+1=3,
当y=0时,x+1=0,解得x=﹣1,
∴A点坐标为(﹣1,0);
(2)由(1)可知B点坐标为(2,3),
把B点坐标代入y2=kx可得3=2k,解k=![]() ,
,
∴y2=![]() x,其图象为过原点的直线,
x,其图象为过原点的直线,
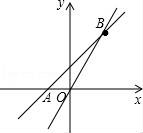
函数y2=![]() x图象如图所示,
x图象如图所示,
当x=2时,y1=y2,
当x>2时,y1<y2,
当x<2时,y1>y2.
【点评】本题主要考查函数图象的交点问题,掌握函数图象上点的坐标满足函数解析式是解题的关键.
24.如图,折线ABC是甲地向乙地打长途电话所需要付的电话费y(元)与通话时间t(分钟)之间关系的图象(注意:通话时间不足1分钟按1分钟计费).
(1)通话1分钟,要付电话费多少元?通话5分钟要付多少电话费?
(2)通话多少分钟内,所支付的电话费一样多?
(3)通话3.2分钟应付电话费多少元?

【考点】一次函数的应用.
【分析】(1)观察图象,可知当0<t≤3时,y=2.5,得出t=1时对应的y值;C点的纵坐标的值即为通话5分钟时要付的电话费;
(2)此段时间内所付电话费不因为时间而改变,即图象与横轴平行,得出结果;
(3)当t≥3时,y是t的一次函数,用待定系数法求出解析式,把t=4代入,求出答案.
【解答】(秦皇岛中考数学)解:(1)根据图象可知,通话1分钟时,要付电话费2.5元,通话5分钟时,要付费4.5元;
(2)根据图象可知,通话3分钟内,所支付的电话费一样多;
(3)当t>3时,设y=kt+b
把B(3,2.5),C(5,4.5)代入
得![]()
解得![]() ,
,
y=t﹣0.5
当T=3.2时,y=4﹣0.5=3.5,
故当t=3.2分钟时,电话费是3.5元.
【点评】此题比较复杂,关键是正确理解题意,然后分析图形要分清不同时间段,电话费的不同找出函数关系式进行解答.
25.抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库.已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A、B两库的路程和运费如下表:(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
| 路程(千米) | 运费(元/吨•千米) | ||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
【考点】一次函数的应用.
【分析】弄清调动方向,再依据路程和运费列出y(元)与x(吨)的函数关系式,最后可以利用一次函数的增减性确定“最省的总运费”.
【解答】解:(1)依题意有:若甲库运往A库粮食x吨,则甲库运到B库(100﹣x)吨,乙库运往A库(70﹣x)吨,乙库运到B库(10+x)吨.
则 ,解得:0≤x≤70.
,解得:0≤x≤70.
y=12×20x+10×25(100﹣x)+12×15(70﹣x)+8×20×[110﹣(100﹣x)]
=﹣30x+39200
其中0≤x≤70
(2)(秦皇岛中考数学)上述一次函数中k=﹣30<0
∴y随x的增大而减小
∴当x=70吨时,总运费最省
最省的总运费为:﹣30×70+39200=37100(元)
答:从甲库运往A库70吨粮食,往B库运送30吨粮食,从乙库运往A库0吨粮食,从乙库运往B库80吨粮食时,总运费最省为37100元.
【点评】本题是一次函数与不等式的综合题,先解不等式确定自变量的取值范围,然后依据一次函数的增减性来确定“最佳方案”.
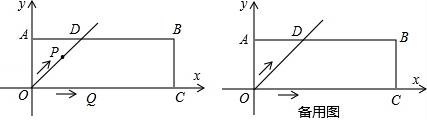
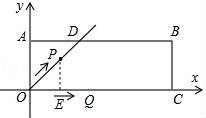
26.在平面直角坐标系xOy中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒![]() 个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.
个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.
(1)当点P移动到点D时,t= 2 秒;
(2)连接点A,C,求直线AC的解析式;
(3)若点M是直线AC上第一象限内一点,是否存在某一时刻,使得四边形OPMQ为平行四边形?若存在,请直接写出t的值及点M的坐标;若不存在,请说明理由.
【考点】一次函数综合题.
【分析】(1)根据矩形以及角平分线的性质可得出△OAD为等腰直角三角形,再根据点A的坐标结合等腰直角三角形的性质即可得出OD的长度,从而可得出t值;
(2)设直线AC解析式为y=kx+b,根据点A、C的坐标利于待定系数法即可求出直线AC的解析式;
(3)假设存在,找出点P、O、Q三点的坐标,根据平行四边形的性质﹣﹣对角线互相平分,分别以OP、OQ、PQ为对角线求出点M的坐标,再根据点M是直线AC上第一象限内一点,即可求出t值以及点M的坐标.
【解答】(秦皇岛中考数学)解:(1)∵四边形OABC为矩形,且∠AOC的平分线交AB于点D,
∴△OAD为等腰直角三角形,
∵点A(0,2),
∴OA=2,OD=2![]() ,
,
点P移动到点D时,t=2![]() ÷
÷![]() =2(秒).
=2(秒).
故答案为:2.
(2)设直线AC解析式为y=kx+b,
将点A(0,2)、C(6,0)代入y=kx+b中,
得:![]() ,解得:
,解得: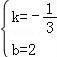 ,
,
∴直线AC解析式为y=﹣![]() x+2.
x+2.
(3)假设存在,过点P作PE⊥x轴于点E,如图所示.
由(1)可知△POE为等腰直角三角形,
∴点P(t,t).
O(0,0),Q(2t,0).
四边形OPMQ为平行四边形分三种情况:
①以OP为对角线时,点M(0+t﹣2t,0+t﹣0),即(﹣t,t),
∵点M在第一象限,
∴此情况不符合要求;
②以OQ为对角线时,点M(0+2t﹣t,0+0﹣t),即(t,﹣t),
∵点M在第一象限,
∴此情况不符合要求;
③以PQ为对角线时,点M(t+2t﹣0,t+0﹣0),即(3t,t),
∵点M在第一象限内,且点M在直线AC上,
∴t=﹣![]() ×3t+2,解得:t=1,
×3t+2,解得:t=1,
此时点M的坐标为(3,1).
综上可知:若点M是直线AC上第一象限内一点,存在某一时刻,使得四边形OPMQ为平行四边形,此时t=1,点M的坐标为(3,1).
【点评】本题考查了矩形的性质、等腰直角三角形的性质、待定系数法求函数解析式以及平行四边形的性质,解题的关键是:(1)求出线段OD的长;(2)利用待定系数法求出函数解析式;(3)分三种情况讨论.本题属于中档题,难度不大,解决该题型题目时,根据平行四边形的性质﹣﹣对角线互相平分,由平行四边形的三个顶点坐标求出第四个顶点的坐标是关键.