请选择
![]() 2018年武汉中考数学压轴真题【精编Word版可下载】
2018年武汉中考数学压轴真题【精编Word版可下载】
由于格式问题,部分试题会存在乱码的现象,请考生点击全屏查看!
第Ⅰ卷(选择题 共30分)
一、选择题(每小题3分,共30分)
下列图形中是中心对称图形的有( )个
A.1 B.2 C.3 D.4
下列一元二次方程中没有实数解的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
关于x的一元二次方程![]() 有两个相等的实数根,则k的值是( )
有两个相等的实数根,则k的值是( )
A.2 B.-2 C.4 D.-4
要得到![]() 的图像,需要抛物线
的图像,需要抛物线![]() 作如下平移( )
作如下平移( )
A.向右平移2个单位,再向上平移3个单位
B.向右平移2个单位,再向下平移3个单位
C.向左平移2个单位,再向上平移3个单位
D.向左平移2个单位,再向下平移3个单位
一个正多边形的每个外角都等于30°,那么这个正多边形的中心角为( )
A.15° B.30° C.45° D.60°
下列说法错误的是( )
A.某种彩票的中奖率为1%,买100张彩票一定有1张中奖
B.从装有10个红球的袋子中,摸出1个白球是不可能事件
C.为了解一批日光灯的使用寿命,可采用抽样调查的方式
D.掷一枚普通的正六面体骰子,出现向上一面点数是2的概率是![]()
某机械长今年生产零件50万个,计划明后两年共生产零件132万个,设该厂每年的平均增长率为x,那么x满足方程( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
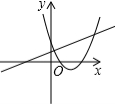
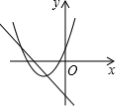
在同一平面直角坐标系中,函数![]() 和函数
和函数![]() (m是常数,且m
(m是常数,且m![]() 0)图像 可能是( )
0)图像 可能是( )

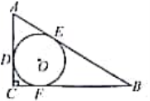
如图,Rt△ABC中,∠C=90°,内切圆⊙O与其三边的切点分别为D、E、F,若AB、BC、AC的长分别为c、a、b,且AE![]() BE =m,a+b+c=n,则⊙O的半径r的值为( )
BE =m,a+b+c=n,则⊙O的半径r的值为( )
![]() B.
B.![]() C.
C.![]() D.
D.![]()
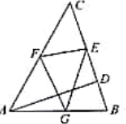
如图,在△ABC中,∠BAC=60°,ADBC于D,且AD=![]() ,E、F、G分别为边BC、CA、AB上的点,则EFG周长的最小值( )
,E、F、G分别为边BC、CA、AB上的点,则EFG周长的最小值( )
A.![]() B.
B.![]() C.3 D.
C.3 D.![]()
二、填空题(每小题3分,共18分)
点M与点N关于原点对称,则a+b=________.
x=1是方程![]() 的一个解,则方程的另一个解是________.
的一个解,则方程的另一个解是________.
武汉市木兰某景区观赏人数逐年增加,据统计,2014约为30万人次,2016年约为2808万人次,设观赏人数年均增长率为x,则列出方程________.
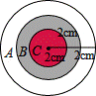
在如图所示(A、B、C三个区域)的图形中随机地撒一把豆子,豆子落在_____区域的可能性最大(填A或B或C) .
已知正六边形的边长为2,则它的内切圆的半径为________.
二次函数![]() 的图像与直线
的图像与直线![]() 和
和![]() 在0≤x≤2内各有一个公共点,则m的取值范围是________.
在0≤x≤2内各有一个公共点,则m的取值范围是________.
三、解答题(共8小题,共72分)
解方程:![]() .
.
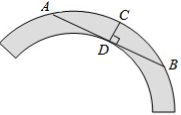
(本题8分)如图是一个古代车轮的碎片,小明为求其外圆半径,连结外圆上的两点A、B,并使AB与车轮内圆相切于点D,作CD垂直AB交外圆于点C,测得CD=10cm,AB=60cm,求这个车轮的外圆半径.
(本题8分)不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(除颜色外其余都相同),其中红球2个,篮球1个,若从中任意摸出一个球,它是蓝球的概率为0.25.
(1)求袋中黄球的个数;
(2)第一次任意摸出一个球(不放回),第二次在摸一个球,请用画树状图或列表格的方法,球两次摸到不同颜色球的概率.
(本题8分)如图,△ABC三个顶点的坐标分别为A(1,1) ,B (4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)若△ABC绕点(2,0)逆时针旋转90°,则B′(,),C′(,).
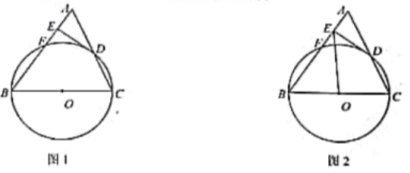
(本题8分)如图1,△ABC中,以BC为直径的⊙O分别与AB、AC交于F、D,过D作DE垂直AB于E,且AE=FE.
(1)求证:DE是⊙O的切线;
(2)如图2,连OE,若OE=![]() ,BC=12,求AE的长.
,BC=12,求AE的长.
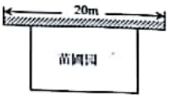
(本题10分)某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成,已知墙长为20米,(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃的面积为108平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于72平方米时,直接写出x的取值范围.
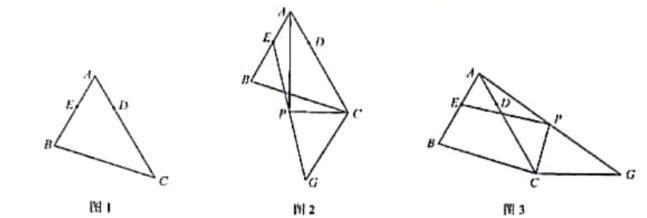
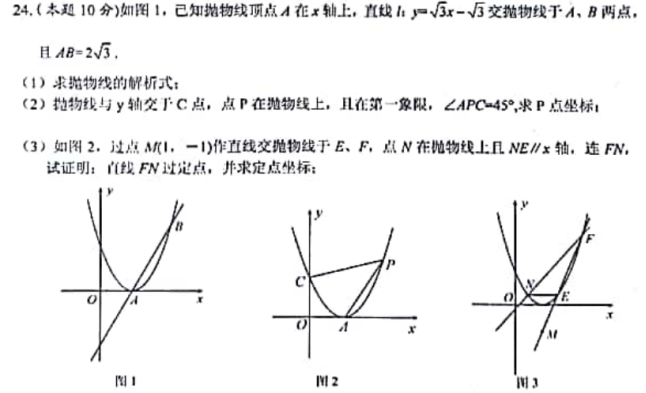
(本题10分)如图1,△ABC中,∠BAC=60°,D、E分别为AC、AB边上两点,且CD=AB,AD=AE,将线段CD绕点C逆时针旋转![]() 角至CG.
角至CG.
(1)如图2,当![]() =120°时,连EG取EG中点P,连AP,CP,求证:AP垂直CP;
=120°时,连EG取EG中点P,连AP,CP,求证:AP垂直CP;
(2)如图3,当![]() =240°时,连AG,取AG中点P,连EP,CP,试判断EP于CP的关系,并证明;
=240°时,连AG,取AG中点P,连EP,CP,试判断EP于CP的关系,并证明;
(3)在图1中,连BD,取BD中点Q,连AQ,则![]() =________.
=________.