请选择
2018年临汾中考数学冲刺试卷【精选word版 可下载】
由于格式问题,部分试题会存在乱码的现象,请考生点击全屏查看!
一、选择题(本大题共10个小题,每小题3分,共30分.)
1.计算![]() 的结果是( )
的结果是( )
A.-3 B.-1 C.1 D.3
2. 将点 A(1,-1)向上平移 2 个单位后,再向左平移 3 个单位,得到点 B,则点 B 的坐标为
A.(-2,1) B.(-2,-1) C.(2,1) D.(2,-1)
3.在体育课上,甲,乙两名同学分别进行了5次跳远测试,经计算他们的平均成绩相同.若要比较这两名同学的成绩哪一个更为稳定![]() ,通常需要比较他们成绩的( )
,通常需要比较他们成绩的( )
A.众数 B.平均数 C.中位数 D.方差
4.某校九年级(1)班在举行元旦联欢会时,班长觉得快要![]() 毕业了,决定临时增加一个节目:班里面任意两名同学都要握手一次.小张同学统 计了一下,全班同学共握手了 465 次.你知道九年级(1)
毕业了,决定临时增加一个节目:班里面任意两名同学都要握手一次.小张同学统 计了一下,全班同学共握手了 465 次.你知道九年级(1)
班有多少名同学吗? 设九年级(1)班有 x 名同学,根据题意列出的方程是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5.下列运算错误的是( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
6.如图,将矩形纸片![]() 沿
沿![]() 折叠,得到
折叠,得到![]() ,
,![]() 与
与![]() 交于点
交于点![]() .若
.若![]() ,则
,则![]() 的度数为( )
的度数为( )
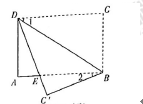
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
7.如图,在正方形 ABCD 中,点 E,F 分别在边 BC,CD 上,且 BE=CF.连接 AE,BF,AE 与BF 交于点 G.下列结论错误的是
A. AE=BF B. ∠DAE=∠BFC
C. ∠AEB+∠BFC=90° D. AE⊥BF

8. 如图所示,线段 AB 切⊙O 于点 A,连接 OA,O![]() B,OB 与⊙O 交于点 C.若 OC=BC=2,则 图中阴影部分的面积为
B,OB 与⊙O 交于点 C.若 OC=BC=2,则 图中阴影部分的面积为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
9.公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数![]() ,导致了第一次数学危机.
,导致了第一次数学危机.![]() 是无理数的证明如下:
是无理数的证明如下:
假设![]() 是有理数,那么它可以表示成
是有理数,那么它可以表示成![]() (
(![]() 与
与![]() 是互质的两个正整数).于是
是互质的两个正整数).于是![]() ,所以,
,所以,![]() .于是
.于是![]() 是偶数,进而
是偶数,进而![]() 是偶数.从而可设
是偶数.从而可设![]() ,所以
,所以![]() ,于是可得
,于是可得![]() 也是偶数.这与“
也是偶数.这与“![]() 与
与![]() 是互质的两个正整数”矛盾,从而可知“
是互质的两个正整数”矛盾,从而可知“![]() 是有理数”的假设不成立,所以,
是有理数”的假设不成立,所以,![]() 是无理数.
是无理数.
这种证明“![]() 是无理数”的方法是( )
是无理数”的方法是( )
A.综合法 B.反证法 C.举反例法 D.数学归纳法
10.如图所示, 在菱形 ABCD 中,∠A=60°,AB=2,E,F 两点分别从A,B 两点同时出发,以相同的速度分别向终点 B,C 移动,连接EF.在移动的过程中,EF 的最小值为( )
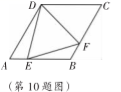
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
二、填空题(本大题共5个小题,每小题3![]() 分,共15分)
分,共15分)
11.计算:![]() .
.
12.如图,已知![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() .将
.将![]() 向右平移4个单位,得到
向右平移4个单位,得到![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]() ,再将
,再将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]() ,则点
,则点![]() 的坐标为 .
的坐标为 .
13. 如图是一组有规律的图案,它们是由边长相同的小正方形组成,第(1)个图案有2个正方形,第(2)个图案共有5个正方形,第(3)个图案共有8个正![]() 方形,…,依此规律,第n(n>1)个图案共有 个正方形(用含n的代数式表示).
方形,…,依此规律,第n(n>1)个图案共有 个正方形(用含n的代数式表示).

14. ![]() 如图,已知反比例函数y=
如图,已知反比例函数y= ![]() 的图象经过点A(3,2),直线l经过点A,
的图象经过点A(3,2),直线l经过点A,![]() 与反比例函数y=的图象 的另外一个 交点为 B,与x轴 的正半轴交 于点C,且AB=2AC, 则 点 B的 坐 标 为 .
与反比例函数y=的图象 的另外一个 交点为 B,与x轴 的正半轴交 于点C,且AB=2AC, 则 点 B的 坐 标 为 .
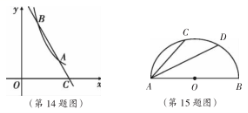
15. 如图所示,半圆O的直径AB=10 cm,弦AC=6 cm.将半圆沿着过点A的直线折叠,折叠后 使得弦AC恰好落在直径AB上.则折痕AD的长为 cm.
16.如图,创新小组要测量公园内一棵树的高度![]() ,其中一名小组成员站在距离树10米的点
,其中一名小组成员站在距离树10米的点![]() 处,测得树顶
处,测得树顶![]() 的仰角为
的仰角为![]() .已知测角仪的架高
.已知测角仪的架高![]() 米,则这颗树的高度为 米(结果保留一位小数.参考数据:
米,则这颗树的高度为 米(结果保留一位小数.参考数据:![]() ,
,![]() ,
,![]() ).
).

17.一副三角板按如图方式摆放,得到![]() 和
和![]() ,其中
,其中![]() ,
,![]() ,
,![]() .
.![]() 为
为![]() 的中点,过点
的中点,过点![]() 作
作![]() 于点
于点![]() .若
.若![]() ,则
,则![]() 的长为
的长为 ![]() .
.
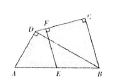
三![]() 、解答题
、解答题![]() (本大题共8个小题,共75分.)
(本大题共8个小题,共75分.)
18.(1)计算:![]() .
.
(![]() 2)分解因式:
2)分解因式:![]() .
.
19.(本题6分)如图,在△ABC中,D为边AB上一点,且AD=2BD。
(1)尺规作图:作∠ADE=∠B,DE与AC边交于点E;(保留作图痕迹, 不写作法![]() ,标明字母)
,标明字母)
(2)在按(1)中要求作图的基础上,若AC=10 cm,求AE的长.
20.如图,在平面直角坐标系中,正方形![]() 的顶点
的顶点![]() 与坐标原点重合,其边长为2,点
与坐标原点重合,其边长为2,点![]() ,点
,点![]() 分别在
分别在![]() 轴,
轴,![]() 轴的正半轴上.函数
轴的正半轴上.函数![]() 的图象与
的图象与![]() 交于点
交于点![]() ,函数
,函数![]() (
(![]() 为常数,
为常数,![]() )的图象经过点
)的图象经过点![]() ,与
,与![]() 交于点
交于点![]() ,与函数
,与函数![]() 的图象在第三象限内交于点
的图象在第三象限内交于点![]() ,连接
,连接![]() .
.
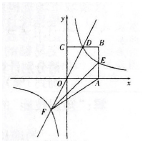
(1)求函数![]() 的表达式,并直接写出
的表达式,并直接写出![]() 两点的坐标.
两点的坐标.
(2)求![]() 的面积.
的面积.
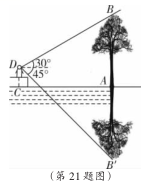
21.(本题9分)如图所示,小华在湖边看到湖中有一棵树 AB,AB与水面AC垂直.此时,小华的眼睛所在 位置D 到湖面的距离DC为4米.她测得树梢B点的仰角为30°,
测得树梢B点在水中的倒影B′点的俯角45°.求树高AB(结果保留根号)
22.如图,![]() 内接于
内接于![]() ,且
,且![]() 为
为![]() 的直径,
的直径,![]() ,与
,与![]() 交于点
交于点![]() ,与过点
,与过点![]() 的
的![]() 的切线交于点
的切线交于点![]() .
.
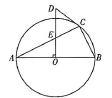
(1)若![]() ,求
,求![]() 的长.
的长.
(2)试判断![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
23.综合与实践
背景阅读 早在三千多年前,我国周朝数学家商高就提出:将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三,股四,弦五”.它被记载于我国古代著名数学著作《周髀算经》中.为了方便,在本题中,我们把三边的比为![]() 的三角形称为(3,4,5)型三角形.例如:三边长分别为9,12,15或
的三角形称为(3,4,5)型三角形.例如:三边长分别为9,12,15或![]() 的三角形就是(3,4,5)型三角形.用矩形纸片按下面的操作方法可以折出这种类型的三角形.
的三角形就是(3,4,5)型三角形.用矩形纸片按下面的操作方法可以折出这种类型的三角形.
实践操作 如图1,在矩形纸片![]() 中,
中,![]() .
.
第一步:如图2,将图1中的矩形纸片![]() 沿过点
沿过点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() ,再沿
,再沿![]() 折叠,然后把纸片展平.
折叠,然后把纸片展平.
第二步:如图3,将图2中的矩形纸片再次折叠,使点![]() 与点
与点![]() 重合,折痕为
重合,折痕为![]() ,然后展平,隐去
,然后展平,隐去![]() .
.
第三步:如图4,将图3中的矩形纸片沿![]() 折叠,得到
折叠,得到![]() ,再沿
,再沿![]() 折叠,折痕为
折叠,折痕为![]() ,
,![]() 与折痕
与折痕![]() 交于点
交于点![]() ,然后展平.
,然后展平.

问题解决
(1)请在图2中证明四边形![]() 是正方形.
是正方形.
(2)请在图4中判断![]() 与
与![]() 的数量关系,并加以证明.
的数量关系,并加以证明.
(3)请在图4中证明![]() 是(3,4,5)型三角形.
是(3,4,5)型三角形.
探索发现
(4)在不添加字母的情况下,图4中还有哪些三角![]() 形是(3,4,5)型三角形?请找出并直接写出它们的名称.
形是(3,4,5)型三角形?请找出并直接写出它们的名称.
24.综合与探究
如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .点
.点![]() 沿
沿![]() 以每秒1个单位长度的速度由点
以每秒1个单位长度的速度由点![]() 向点
向点![]() 运动,同时,点
运动,同时,点![]() 沿
沿![]() 以每秒2个单位长度的速度由点
以每秒2个单位长度的速度由点![]() 向点
向点![]() 运动,当一个点停止运动时,另一个点也随之停止运动,连接
运动,当一个点停止运动时,另一个点也随之停止运动,连接![]() ,过点
,过点![]() 作
作![]() 轴,与抛物线交于点
轴,与抛物线交于点![]() ,与
,与![]() 交于点
交于点![]() .连接
.连接![]() ,与
,与![]() 交于点
交于点![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒(
秒(![]() )
)![]() .
.
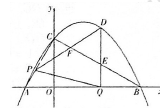
(1)求直线![]() 的函数表达式.
的函数表达式.
(2)①直接写出![]() 两点的坐标(用含
两点的坐标(用含![]() 的代数式表示,结果需化简).
的代数式表示,结果需化简).
②在![]() 点
点![]() 运动的过程中,当
运动的过程中,当![]() 时,求
时,求![]() 的值.
的值.
(3)试探究在点![]() 运动的过程中,是否存在某一时刻,使得点
运动的过程中,是否存在某一时刻,使得点![]() 为
为![]() 的中点.若存在,请直接写出此时
的中点.若存在,请直接写出此时![]() 的值与点
的值与点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.