请选择
2018邵阳中考数学模拟压轴真题【精编Word版】
由于格式问题,部分试题会存在乱码的现象,请考生点击全屏查看!
一、选择题(每小题3分,共30分)
1.下列运算正确的是( )
A.(a﹣b)2=a2﹣b2 B.(a+b)(a﹣b)=a2﹣b2 C.(a3)2=a5 D.a3÷a3=a
2.如果一个正多边形的内角和为720°,那么这个正多边形的每一个外角是( )
A.60° B.120° C.135° D.45°
3.用配方法解一元二次方程x2﹣4x=5时,此方程可变形为( )
A.(x+2)2=1 B.(x﹣2)2=1 C.(x+2)2=9 D.(x﹣2)2=9
4.下列全国各地地铁标志图中,既是轴对称图形又是中心对称图形的是( )
A.![]() B.
B.![]() C.
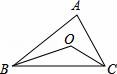
C. D.
D.
5.如图,AB为⊙O直径,CD为弦,AB⊥CD,如果∠BOC=70°,
那么∠A的度数为( )
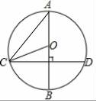
A.70° B.35° C.30° D.20°
6.已知圆锥的底面半径为4cm,母线长为5cm,则这个圆锥的侧面积是( )
A.20πcm2 B.20cm2 C.40πcm2 D.40cm2
7.函数y=kx+1与函数![]() 在同一坐标系中的大致图象是( )
在同一坐标系中的大致图象是( )
![]() A.
A. B.
B. C.
C.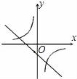 D.
D.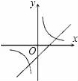
8.某天,学校研究性学习小组的同学从8时起骑自行车外出调查,17时回到学校,小组离开学校的距离与时间的关系可用图中的曲线表示,根据这个曲线图,下列说法错误的是( )
A.在离校最远的地方调查的时间是14~15时
B.第一次调查从9时开始,历时2h
C.中午12~![]() 13时休息的地方离校15km
13时休息的地方离校15km
D.返校的速度最慢
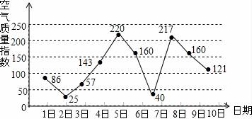
9.如图是某市某月1日至10日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示![]() 空气重度污染,某人随机选择7月1日至7月8日中的某一天到达该市
空气重度污染,某人随机选择7月1日至7月8日中的某一天到达该市![]() ,并连续停留3天.则此人在该市停留期间有且仅有1天空气质量重度污染的概率是( )
,并连续停留3天.则此人在该市停留期间有且仅有1天空气质量重度污染的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.如图,△AOB为等腰三角形,顶点A的坐标(2,![]() ),底边OB在x轴上.
),底边OB在x轴上.![]() 将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )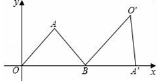
A.(![]() ,
,![]() ) B.(
) B.(![]() ,
,![]() ) C.(
) C.(![]() ,
,![]() ) D.(
) D.(![]() ,4
,4![]() )
)
二、填空题(每小题3分,共30分)
11.Rt△ABC中,∠C=90°,∠A=35°30′,则∠B= °.
12.三角形的中位线把三角形分成两部分面积之比是 .
13.已知O为△ABC的内心,且∠BOC=130°,则∠A= .
14![]() .从﹣4、﹣2、0、2、4这5个数中任取一个数,
.从﹣4、﹣2、0、2、4这5个数中任取一个数,![]() 作为关于x的一元二次方程x2+kx+4=0的k值,则所得的方程中有两个相等的实数根的概率是 .
作为关于x的一元二次方程x2+kx+4=0的k值,则所得的方程中有两个相等的实数根的概率是 .
15.一组数据按从小到大的顺序排列为1,2,3,3,4,5,
则这组数据的方差是 .
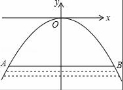
16.拱桥截![]() 面是一条抛物线,如图所示,现测得水面宽AB=16m,
面是一条抛物线,如图所示,现测得水面宽AB=16m,
拱顶O到水面的距离为8m,在图中的直角坐标系内,拱桥所
在抛物线的解析式是 .
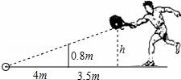
17.如图,小明在打网球时,使球恰好能打过网,而且落在
离网4米的位置上,则球拍击球的高度h为
18.已知关于x的方程![]() 的解是正数,则m的范围是 .
的解是正数,则m的范围是 .
19.环境空气质量问题已经成为人们日常生活所关心的重要问题,我国新修订的《环境空气质量标准》中增加了PM2.5检测指标,“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物,2.5微米即0.0000025米,用科学记数法表示0.0000025是 _.
20.一辆货车从甲地匀速驶往乙地,到达后用了半小时卸货,随即匀速返回,已知货车返回的速度是它从甲地驶往乙地的速度的1.5倍.货车离甲地的距离y(千米)关于时间x(小时)的函数图象如图所示.则a= (小时).

三、解答题(共60分)
21.计算:(![]() )﹣2﹣20150+
)﹣2﹣20150+![]() ÷
÷![]() ﹣2sin45°.
﹣2sin45°.
22.已知x=1,y=﹣2.求![]() ÷(x﹣y)﹣
÷(x﹣y)﹣![]() 的值.
的值.
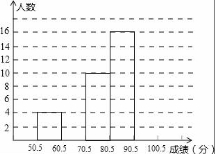
23.为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保![]() 知识竞赛”,共有850名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)进行统计.请你根据尚未完成并有局部污染的频率分布表和频率分布直方图,解答下列问题:(1)填充频率分布表的空格;
知识竞赛”,共有850名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)进行统计.请你根据尚未完成并有局部污染的频率分布表和频率分布直方图,解答下列问题:(1)填充频率分布表的空格;
(2)补全频数直方图,并在此图上直接绘制频数分布折线图;
(3)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?
(4)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
分 组 | 频数 | 频率 |
50.5~60.5 | 4 | 0.08 |
60.5~70.5 |
| 0.16 |
70.5~80.5 | 10 |
|
80.5~90.5 | 16 | 0.32 |
90.5~100.5 |
|
|
合 计 | 50 | 1.00 |
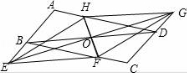
24.如图,过平行四边形ABCD的对角线BD的中点O作两条互相垂直的直线,且交AB、CD的延长线于点E,G,交BC,AD于点F,H,连接EF,FG,GH,EH
(1)求证:△BEO≌△DGO;(2)试判断![]() 四边形EFGH的形状,并说明理由.
四边形EFGH的形状,并说明理由.
25.在我国民间流传着许多诗歌形式的数学算题,这些题目叙述生动、活泼,它们大都是关于方程或方程组的应用题.由于诗歌的语言通俗易懂、雅俗![]() 共赏,因而一扫纯数学的枯燥无味之感,令人耳目一新,回味无穷.请根据下列诗意列方程组解应用题.
共赏,因而一扫纯数学的枯燥无味之感,令人耳目一新,回味无穷.请根据下列诗意列方程组解应用题.
(1)周瑜寿属:而立之年督东吴,早逝英年两位数;十比个位正小三,个位六倍与寿符;哪位同学算得快,多少年寿属周瑜?诗的意思是:周瑜病逝时的年龄是一个大于30的两位数,其十位数上的数字比个位上的数字小3,![]() 个位上的数字的6倍正好等于这个两位数,求这个两位数.
个位上的数字的6倍正好等于这个两位数,求这个两位数.
(2)悟空顺风探妖踪,千里只用四分钟,归时四分行六百,风速多少请算清.
26.某学校计划用180 000元从厂家那里购买A型、B型、C型三种型号的电脑,其中A型出厂价为5 400元,B型出厂价为3 600元,C型出厂价为1 800元.
(1)若学校同时购进其中两种不同型号的电脑共40部,并将180 000元恰好用完.请你帮助![]() 学校计算一下如何购买;
学校计算一下如何购买;
(2)若学校同时购进三种不同型号的电脑共40部,并将180 000元恰好用![]() 完,并且要求C型电脑的购买数量不少于6部且不多于8部,请你设计几种不同购买方案供学校选择,并说明理由.
完,并且要求C型电脑的购买数量不少于6部且不多于8部,请你设计几种不同购买方案供学校选择,并说明理由.
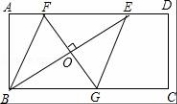
27.如图,矩形ABCD中,AD=2AB,E是AD边上一点,![]() AD(n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.
AD(n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.
(1)试判断四边形B![]() FEG的形状,并说明理由;
FEG的形状,并说明理由;
(2)当AB=a(a为常数),n=3时,求FG的长;
(3)记四边形BFEG的面积为S1,矩形ABCD的面积为S2,当![]() 时,求n的值.(直接写出结果,不必写出解答过程)
时,求n的值.(直接写出结果,不必写出解答过程)
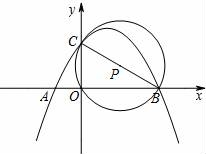
28.如图,抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0)、B(3,0)、C(0,![]() )三点.
)三点.
(1)求抛物线的函数表达式;(2)求证:点C在以AB为直径的圆上;
(3)以BC为直径作⊙P,点D为抛物线上一动点,是否存在点D使直线OD与⊙P相切?若存在,请求出点D的坐标;若不存在,请说明理由.