平面平行的性质定理

1、两平面平行，其中一个平面内的直线必平行于另一个平面。2、如果两个平行平面同时和第三个平面相交，那么它们的交线平行。3、一条直线垂直于两个平行平面中的一个平面，它也垂直于另一个平面。

两平面平行定义

两平面平行是两平面间的一种位置关系，如果两个平面没有公共点，我们说这两个平面互相平行，一个平面称为另一个平面的平行平面。

证明

如图，在正方体ABCD-A₁B₁C₁D₁中，M，N，P分别是C₁C，B₁C₁，C₁D₁的中点，求证：

(1)AP⊥MN；

(2)平面MNP∥平面A1BD。

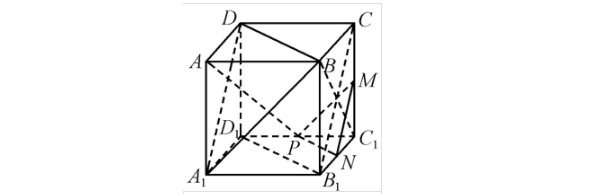
证明(1)连结BC₁，B₁C，则B₁C⊥BC₁，BC₁是AP在面BB₁C₁C上的射影，

∴AP⊥B1C.

又B1C∥MN，

∴AP⊥MN.

(2)连结B₁D₁.

∵P，N分别是D₁C₁，B₁C₁的中点，

∴PN∥B₁D₁.又B₁D₁∥BD，

∴PN∥BD.

又PN不在平面A1BD上，

∴PN∥平面A₁BD.

同理，MN∥平面A₁BD.

又PN∩MN=N，

∴平面PMN∥平面A₁BD。

说明将空间问题转化为平面问题，是解决立体几何问题的重要策略.解决这类问题关键在于选择或添加适当的平面或线。由于M，N，P都为中点，故添加B1C，BC1作为联系的桥梁。