二项式定理系数

二项式定理，又称牛顿二项式定理，由艾萨克·牛顿于1664、1665年间提出。在数学里，二项式系数，或组合数，是定义为形如(1+x)ⁿ展开后x的系数（其中n为自然数，k为整数）。

二项式系数对组合数学很重要，因它的意义是从n件物件中，不分先后地选取k件的方法总数，因此也叫做组合数。从定义出发，把n个(1+x)项的乘积展开，其中任意k项的x和n−k项的1相乘得出一个x，故此x的系数是从n个选取k个的方法总数。把各项的x标记可以更清楚看出：当n=4, k=2时，

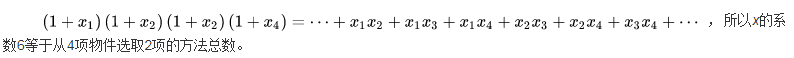
二项式系数是杨辉三角的第n+1行从左起第k+1个数，它最先由杨辉发现。

二项式系数符合等式可以由其公式证出，也可以从其在组合数学的意义推导出来。如第一式左项表示从n+1件选取k件的方法数，这些方法可分为没有选取第n+1件，即是从其余n件选取k件；和有选取第n+1件，即是从其余n件选取k−1件。而第二式则是每个从n件选取k件的方法，也可看为选取其余n−k件的方法。