邻边相等的平行四边形是菱形吗

是的。菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的对角线互相垂直平分且平分每一组对角；菱形是轴对称图形，对称轴有两条，即两条对角线所在直线；菱形是中心对称图形。

求证：有一组邻边相等的平行四边形为菱形，那么由菱形的定义可知：四条边均相等的四边形是菱形。所以，如下图：

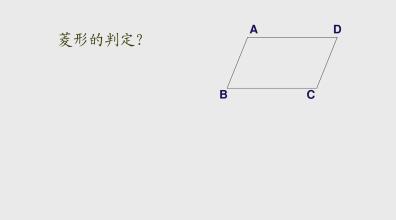
可设在平行四边形ABCD中，AB=BC，求证四边形ABCD是菱形。

证明:

∵四边形ABCD是平行四边形，

∴AB=CD，AD=BC（平行四边形对边相等），

∵AB=BC，

∴AB=BC=CD=AD，

∴四边形ABCD是菱形（原始定义：四条边都相等的四边形叫菱形）。

判定

在同一平面内，

一组邻边相等的平行四边形是菱形；

对角线互相垂直的平行四边形是菱形；

四条边均相等的四边形是菱形；

对角线互相垂直平分的四边形；

两条对角线分别平分每组对角的四边形；

有一对角线平分一个内角的平行四边形；

菱形是在平行四边形的前提下定义的，首先它是平行四边形，而且是特殊的平行四边形，特殊之处就是“有一组邻边相等”，因而增加了一些特殊的性质和判定方法。

菱形的一条对角线必须与x轴平行，另一条对角线与y轴平行。

不满足此条件的几何学菱形在计算机图形学上被视作一般四边形。