请选择
请点击全屏查看
数学试题
一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.-5的倒数是( )
A. ![]() B.
B. ![]() C. 5 D. -5
C. 5 D. -5
2.下列各数中,为无理数的是( )
A. ![]() B.
B. ![]() C.
C.![]() D.
D.![]()
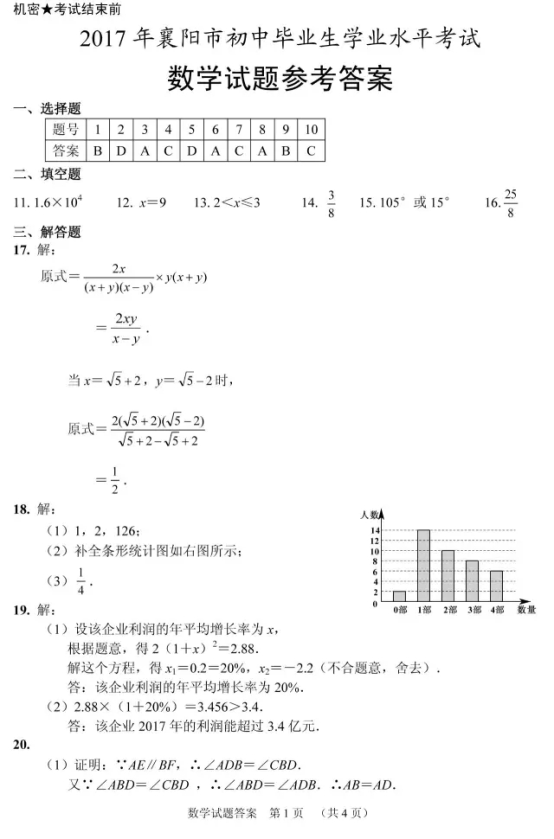
3. (2017襄阳数学)如图,![]() 平分
平分![]() ,交
,交![]()
![]() 于点
于点![]() .若
.若![]() ,则
,则![]() 的度数为( )
的度数为( )
A. 65° B. 60° C.55° D. 50°
4. 下列运算正确的是( )
A.![]()
![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
5. 下列调查中,调查方式选择合理的是(![]() )
)
A.为了解襄阳市初中生每天锻炼所用的时间,选择全面调查
B.为了解襄阳电视台《襄阳新闻》栏目的收视率,选择全面调查
C. 为了解神舟飞船设备零件的质量情况,选择抽样调查
D.为了解一批节能灯的使用寿命,选择抽样调查
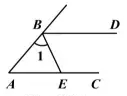
6.(2017襄阳数学) 如图所示的几何体是由6个大小完全一样的正方体组合而成的,它的俯视图是( )
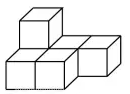
A.
![]() B.
B.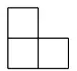 C.
C. 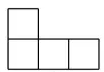 D.
D.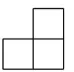
7.下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B.
B.  C.
C.  D.
D.
8. 将抛物线![]() 先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为( )
先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为( )
A. ![]() B.
B.![]() C.
C. ![]() D.
D.![]()
9. (2017襄阳数学)如图,在![]() 中,
中,![]() .以点
.以点![]() 为圆心,
为圆心,![]() 长为半径作弧,交
长为半径作弧,交![]() 于点
于点![]() ;再分别以点
;再分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧相交于点
的长为半径作弧,两弧相交于点![]() ;作射线
;作射线![]() 交
交![]() 于点
于点![]() .则
.则![]() 的长为( )
的长为( )
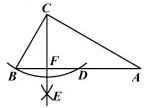
A. 5 ![]() B. 6 C. 7 D.8
B. 6 C. 7 D.8
10. “赵爽弦图”巧妙地利用面积关系证![]() 明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为
明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为![]() ,较短直角边长为
,较短直角边长为![]() ,若
,若![]() ,大正方形的面积为13,则小正方形的面积为( )
,大正方形的面积为13,则小正方形的面积为( )
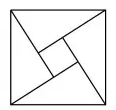
A. 3 B. 4 C. 5 D.6
二、(2017襄阳数学)填空题(本大题共6个小题,每小题3分,共18分,将答案填在答题纸上)
11.某天到襄阳某镇观赏桃花的游客近16000人,数据16000用科学计数法表示为___________.
12.分式方程![]() 的解是____________.
的解是____________.
13.不等式组![]() 的解集为 .
的解集为 .
14.同时抛掷三枚质地均匀的硬币,出现两枚正面向上,一枚正面向下的概率是 .
15.在半径为1的![]() 中,弦
中,弦![]() 的长分别为1和
的长分别为1和![]() ,则
,则![]() 的度数为 .
的度数为 .
16.如图,在![]() 中,
中,![]() ,点
,点![]() 分别在
分别在![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 折
折
叠,点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处,若
处,若![]() ,则
,则![]() 的长为 .
的长为 .
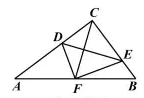
三、(2017襄阳数学)解答题 (本大题共9小题,共72分.解答应写出文字说明、证明过程或演算步骤.)
17.先化简,再求值:![]() ,其中
,其中![]() .
.
18.中华文化,源远流长.在文学方面,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查.根据调查结果绘制成如所示的两个不完整的统计图,请结合图中信息解决下列问题:
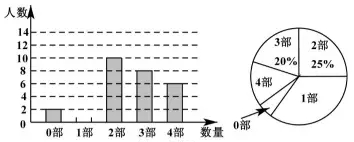
(1)本次调查所得数据的众数是____________部,中位数是___________部;扇形统计图中“1部”所在扇形的圆心角为____________度;
(2)请将条形统计图补充完整;
(3)没有读过四大名著的两名学生准备从四大古典名著中各自随机选择一部来阅读,则他们选中同一名著的概率为______________.
19.受益于国家支持新能源汽车发展和“一带一路”发展战略等多重利好因素,我市某汽车零部件生产企业的利润逐年提高.据统计,2014年利润为2亿元,2016年利润为2.88亿元.
(1)求该企业从2014年到2016年利润的年平均增长率;
(2)若2017年保持前两年利润的年平均增长率不变,该企业2017年的利润能否超过3.4亿元?
20.(2017襄阳数学)如图,![]() ,
,![]() 平均
平均![]() ,且交
,且交![]() 于点
于点![]() 平分
平分![]() ,且交
,且交![]() 于点
于点![]() ,连接
,连接![]() .
.
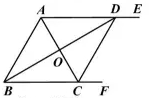
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,求
,求![]() 的长.
的长.
21. 如图,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的纵坐标为6,点
的纵坐标为6,点![]() 的坐标为
的坐标为![]() .
.
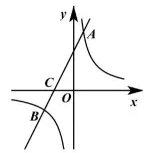
(1)求直线和双曲线的解析式;
(2)求点![]() 的坐标,并结合图象直接写出
的坐标,并结合图象直接写出![]() 时
时![]() 的取值范围.
的取值范围.
22.(2017襄阳数学)如图,![]() 为
为![]() 的直径,
的直径,![]() 为
为![]() 上两点,
上两点,![]() ,过点
,过点![]() 作直线
作直线![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
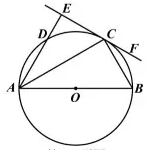
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,求劣弧
,求劣弧![]() 的长
的长![]() .
.
23. 为了“创建文明城市,建设美丽家园”,我市某社区将辖![]() 区内的一块面积为
区内的一块面积为![]() 的空地进行绿化,一部分种草,剩余部分栽花.设种草部分的面积为
的空地进行绿化,一部分种草,剩余部分栽花.设种草部分的面积为![]() ,种草所需费用
,种草所需费用![]() (元)与
(元)与![]() 的函数关系式为
的函数关系式为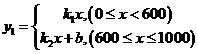 ,其图象如图所示;栽花所需费用
,其图象如图所示;栽花所需费用![]() (元)与
(元)与![]() 的函数关系式
的函数关系式![]() .
.
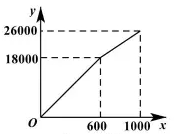
(1)请直接写出![]() 和
和![]() 的值;
的值;
(2)设这块![]() 空地的绿化总费用为
空地的绿化总费用为![]() (元),请利用
(元),请利用![]() 与
与![]() 的函数关系式,求出绿化总费用
的函数关系式,求出绿化总费用![]() 的最大值;
的最大值;
(3)若种草部分的面积![]() 不少于
不少于![]() ,栽花部分的面积不少于
,栽花部分的面积不少于![]() ,请求出绿化总费用
,请求出绿化总费用![]() 的最小值.
的最小值.
24.如图,在![]() 中,
中,![]() ,
,![]() 是中线,
是中线,![]() .一个以点
.一个以点![]() 为顶点的45°角绕点
为顶点的45°角绕点![]() 旋转,使角的两边分别与
旋转,使角的两边分别与![]() 的延长线相交,交点分别为点
的延长线相交,交点分别为点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
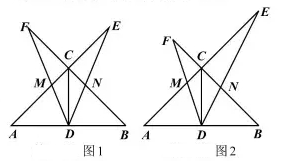
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
(2)如图2,在![]() 绕点
绕点![]() 旋转的过程中:
旋转的过程中:
①探究三条线段![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
②若![]() ,求
,求![]() 的长.
的长.
25.(2017襄阳数学)如图,矩形![]() 的两边在坐标轴上,点
的两边在坐标轴上,点![]() 的坐标为
的坐标为![]() ,抛物线
,抛物线![]() 过
过![]() 两点,且与
两点,且与![]() 轴的一个交点为
轴的一个交点为![]() ,点
,点![]() 是线段
是线段![]() 上的动点,设
上的动点,设![]() .
.
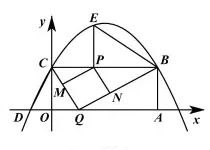
(1)请直接写出![]() 两点的坐标及抛物线的解析式;
两点的坐标及抛物线的解析式;
(2)过点![]() 作
作![]() ,交抛物线于点
,交抛物线于点![]() ,连接
,连接![]() ,当
,当![]() 为何值时,
为何值时,![]() ?
?
(3)点![]() 是
是![]()
![]() 轴上的动点,过点
轴上的动点,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,作
,作![]() ,交
,交![]() 于点
于点![]() .当
.当![]() 四边形
四边形![]() 为正方形时,请求出
为正方形时,请求出![]() 的值.
的值.