请选择
各位同学在查看时请点击全屏查看
2018年太原中考数学模拟试题
(满分:120分 时间:120分钟)
第Ⅰ卷 选择题(共30分)
一、模拟试题选择题(本大题共10小题,每小题3分,共30分)
1.-的倒数是( B )
A.- B.-![]() C. D.
C. D.
2.由2016年8月25日上午召开的教育部新闻发布会上获悉,去年我国学生资助资金继续保持增长势头,首次突破1500亿元,增长近10%,将“1500亿”用科学记数法表示为( C )
A.1.5×1010 B.15.0×109 C.1.5×1011 D.15.0×1011
3.下列运算正确的是( D )
A.(ab)2=ab2 B.3a+2a2=5a2 C.2(a+b)=2a+b D.a·a=a2
4.如图是由5个相同的小正方体组成的立体图形,这个立体图形的俯视图是( C )

5.下列说法正确的是( C )
A.为了审核书稿中的错别字,选择抽样调查
B.为了了解春节联欢晚会的收视率,选择全面调查
C.“射击运动员射击一次,命中靶心”是随机事件
D.“经过有交通信号灯的路口,遇到红灯”是必然事件
6.甲、乙两人进行飞镖比赛,每人各投5次,所得平均环数相等,其中甲所得环数的方差为15,乙所得环数如下:0,1,5,9,10,那么成绩较稳定的是( A )
A.甲 B.乙 C.都一样 D.无法确定
7.根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”、“无字证明”可用于验证数与代数、
图形与几何等领域中的许多数学公式和规律,体现了数形结合的思想方法,展现了数学美,上面图形验证的内容是( B )
A.乘法公式 B.勾股定理
C.直角三角形中的三角函数 D.中位线定理
8.按照山西省“改薄工程”规划,我省5年投入85亿元用于改造农村县(市、区)薄弱学校,促进义务教育均衡发展,其中某项“改薄工程”建设,甲队单独完成需要20天,若由甲队先做![]() 13天,则剩下的工程由甲、乙两队合作3天完成.问乙队单独完成这项工程需要多少天?若设乙队单独完成这项工程需要x天,根据题意可列方程为( B )
13天,则剩下的工程由甲、乙两队合作3天完成.问乙队单独完成这项工程需要多少天?若设乙队单独完成这项工程需要x天,根据题意可列方程为( B )
A.13+3+x=20 B.+3(+)=1 C.+=1 D.(1-)+x=3
9.关于抛物线y=x2-(a+1)x+a-2,下列说法错误的是( C )
A.开口向上 B.当a=2时,经过坐标原点O[来源:学#科#网Z#X#X#K]
C.a>0时,对称轴在y轴左侧 D.不论a为何值,都经过定点(1,-2)

10.如图,平行四边形AB![]() CD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数y=(x>0)的图象经过点D.已知S△BCE=2,则k的值是( D )
CD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数y=(x>0)的图象经过点D.已知S△BCE=2,则k的值是( D )
A.2 B.-2 C.3 D.4
第Ⅱ卷 非选择题(共90分)
二、填空题(本大题5小题,每小题3分,共15分)
11.已知点P(2-a,2a-7)(其中a为整数)位于第三象限,则点P坐标为__(-1,-1)__.
12.某地体育测试用抽签的方式决定考试分组和考试项目,具体操作流程是:①每位考生从写有A、B、C的三张纸片中随机抽取一张确定考试分组;②再从写有“引体向上”、“立定跳远”、“800米”的三张纸片中随机抽取一张确定考试项目,则考生小明抽到A组“引体向上”的概率等于____.
13.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是2,则点B的横坐标是__-2.5__.
 ,第13题图)
,第13题图) 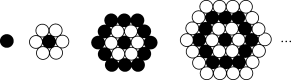 ,第14题图)
,第14题图)  ,第15题图)
,第15题图)
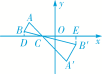
解析:如图,过点B、B′分别作BD⊥x轴于D,B′E⊥x轴于E,∴∠BDC=∠B′EC=90°.∵△ABC的位似图形是△A′B′C,∴点B、C、B′在一条直线上,∴∠BCD=∠B′CE,∴△BCD∽△B′CE.∴=,设点B的横坐标为x,则DC=-1-x,EC=2+1=3,又∵=,∴=,∴2(-1-x)=3,∴x=-2.5,∴点B的横坐标为-2.5.
14.如图,小宇用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成,按照这样的规律排列下去![]() ,则第10个图案中共有__121__个黑子.
,则第10个图案中共有__121__个黑子.
解析:第1、2图案中黑子有1个,第3、4图案中黑子有1+![]() 2×6=13个,第5、6图案中黑子有1+2×6+4×6=37个,第7、8图案中黑子有1+2×6+4×6+6×6=73个,第9、10图案中黑子有1+2×6+4×6+6×6+8×6=121个
2×6=13个,第5、6图案中黑子有1+2×6+4×6=37个,第7、8图案中黑子有1+2×6+4×6+6×6=73个,第9、10图案中黑子有1+2×6+4×6+6×6+8×6=121个
15.如图,在菱形ABCD中,AB=5,AC=8,点P是对角线AC上的一个动点,过点P作EF⊥AC分别交AD、AB于点E、F,将△AEF沿EF折叠,点A落在点A′处,当△A′BC是等腰三角形时,AP的长为__或__.[来源:Z.xx.k.Com]
解析:∵四边形ABCD是菱形,∴AB=BC=CD=AD=5,∠DAC=∠BAC,∵EF⊥AA′,∴∠EPA=∠FPA=90°,∴∠EAP+∠AEP=90°,∠FAP+∠AFP=90°,∴∠AEP=∠AFP,∴AE=AF,∵△A′EF是由△AEF翻折,∴AE=EA′,AF=FA′,∴AE=EA′=A′F=FA,∴四边形AEA′F是菱形,∴AP=PA′.①当CB=CA′时,∵AA′=AC-CA′=3,∴AP=AA′=.②当A′C=A′B时,∵∠A′CB=∠A′BC=∠BAC,∴△A′CB∽△BAC,∴=,∴A′C=,∴A![]() A′=8-=,∴AP=AA′=
A′=8-=,∴AP=AA′=
三、解答题(本大题共8小题,共75分,解答应写出文字说明、证明过程或演算步骤)
16.(本题共2小题,每小题5分,共10分)
(1)计算:(-)-1-|-3|-(3-π)0+2cos45°.
解:原式=-4-3-1+=-8+.
(2)分解因式:(x2-x)2-12(x2-x)+36.
解:原式=(x2-x-6)2=[(x+2)(x-3)]2=(x+2)2(x-3)2
17.(本题7分)解分式方程:-=.
解:原方程可化为3(3x-1)-4x=7,
整理得:5x=10,
解得:x=2,
经检验x=2是原方程的解,
则原分式方程的解为x=2 ![]()
18.(本题7分)近几年来,国家对购买新能源汽车实行补助政策,2016年某省对新能源汽车中的“插电式混合动力汽车”实行每辆3万元的补助,小刘对该省2016年“纯电动乘用车”和“插电式混合动力车”的销售计划进行了研究,绘制出如图所示的两幅不完整的统计图.
(1)补全条形统计图;
(2)求出“D”所在扇形的圆心角的度数;
(3)为进一步落实该政策,该省计划再补助4.5千万元用于推广上述两大类产品,请你预测,该省2016年计划大约共销售“插电式混合动力汽车”多少辆?
注:R为纯电动续航行驶里程,图中A表示“纯电动乘用车”(100km≤R<150km),B表示“纯电动乘用车”(150km≤R<250km),C表示“纯电动乘用车”(R≥250km),D为“插电式混合动力汽车”.
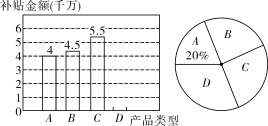
解:(1)补贴总金额为:4÷20%=20(千万元),
则D类产品补贴金额为:20-4-4.5-5.5=6(千万元),补全条形统计图如图:
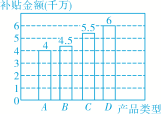
(2)360°×=108°,
答:“D”所在扇形的圆心角的度数为108°;
(3)根据题意,2016年补贴D类“插电式混合动力汽车”金额为:6+4.5×=7.35(千万元),
∴7350÷3=2450(辆),
答:预测该省2016年计划大约共销售“插电式混合动力汽车”2450辆
19.(本题7分)请阅读以下材料,并完成相应的任务.[来源:Z。xx。k.Com]
传说古希腊毕达哥拉斯(Pythagonas,约公元570年-约公元前500年)学派的数学家经常在沙滩上研究数学问题.他们在沙滩上画点或用小石子来表示数,比如,他们研究过1、3、6、10、…,由于这些数可以用如图所示的三角形点阵表示,他们就将其称为三角形数,第n个三角形数可以用(n≥1)表示.

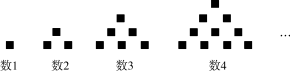
任务:请根据上面材料,证明以下结论.
(1)任意一个三角形数乘8再加1是一个完全平方数;
(2)连续两个三角形数的和是一个完全平方数.
证明:(1)∵×8+1=4n2+4n+1=(2n+1)2,∴任意一个三角形数乘8再加1是一个完全平方数;
(2)∵第n个三角形数为,第n+1个三角形数为,
∴这两个三角形数的和为:+==(n+1)2,
即连续两个三角形数的和是一个完全平方数
20.(本题8分)某校准备组织学生及家长代表到桂林进行社会实践活动,为便于管理,所有人员必须乘坐同一列高铁,高铁单程票价格如表所示,二等座学生票可打7.5折,已知所有人员都买一等座单程火车票需6175元,都买二等座单程火车票需3150元;如果家长代表与教师的人数之比为2∶1.
运行区间 | 票价 |
|
|
起点站 | 终点站 | 一等座 | 二等座 |
都匀 | 桂林 | 95(元) | 60(元) |
(1)参加社会实践活动的老师、家长代表与学生各有多少人?
(2)由于各种原因,二等座单程火车票只能买x张(x<参加社会实践的总人数),其余的须买一等座单程火车票,在保证所有人员都有座位的前提下,请你设计最经济的购票方案,并写出购买单程火车票的总费用y与x之间的函数关系式;
(3)在(2)的方案下,请求出当x=30时,购买单程火车票的总费用.
解:(1)设参加社会实践的老师有m人,学生有n人,则学生家长有2m人,
根据题意得:,
解得:,则2m=10.
答:参加社会实践的老师、家长与学生各有5、10与50人;
(2)由(1)知所有参与人员总共有65人,其中学生有50人,
①当50≤x<65时,最经济的购票方案为:
学生都买学生票共50张,(x-50)名成年人买二等座火车票,(65-x)名成年人买一等座火车票.
∴火车票的总费用(单程)y与x之间的函数关系式为:y=60×0.75×50+60(x-50)+95(65-x),
即y=-35x+5425(50≤x<65);
②当0<x<50时,最经济的购票方案为:一部分学生买学生票共x张,其余的学生与家长老师一起购买一等座火车票共(65-x)张.
∴火车票的总费用(单程)y与x之间的函数关系式为:y=60×0.75x+95(65-x),
即y=-50x+6175(0<x<50),
∴购买单程火车票的总费用y与x之间的函数关系式为:y=;
(3)∵x=30<50,
∴y=-50x+6175=-50×30+6185=4675,[来源:Zxxk.Com]
答:当x=30时,购买单程火车票的总费用为4675元
21.(本题10分)放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段,≈1.414,≈1.732,最后结果精确到1米).
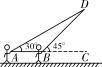
解:如图,作DH⊥BC于H,设DH=x米.
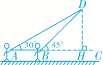
∵∠AHD=90°,
∴在Rt△ADH中,∠DAH=30°,AD=2DH=2x,AH==x,
在Rt△BDH中,∠DBH=45°,BH=DH=x,BD=x,
∵AH-BH=AB=10,
即x-x=10,
∴x=5(+1),
则小明此时所收回的风筝的长度为:
AD-BD=2x-x=(2-)×5(+1)≈(2-1.414)×5×(1.732+1)≈8米.
答:小明此时所收回的风筝线的长度约是8米
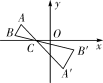
22.(本题12分)△ABC和△DBE是绕点B旋转的两个相似三角形,其中∠ABC与∠DBE、∠A与∠D为对应角.
(1)如图①,若△ABC和△DBE分别是以∠ABC与∠DBE为顶角的等腰直角三角形,且两三角形旋转到使点B、C、D在同一条直线上的位置时,请直接写出线段AD与线段EC的关系;[来源:学科网]
(2)若△ABC和△DBE为含有30°角的直角三角形,且两个三角形旋转到如图②的位置时,试确定线段AD与线段EC的关系,并说明理由;
(3)若△ABC和△DBE为如图③的两个三角形,且∠ACB=α,∠BDE=β,在绕点B旋转的过程中,直线AD与EC夹角的度数是否改变?若不改变,直接用含α、β的式子表示夹角的度数;若改变,请说明理由.
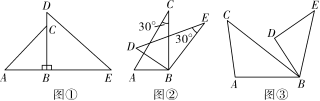
解:(1)线段AD与线段CE的关系是AD⊥EC,AD=EC;
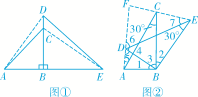
(2)如图②,连接AD、EC并延长,设交点为点F,∵△ABC∽△DBE,∴=,∴=.∵∠ABC=∠DBE=90°,∴∠1+∠3=90°,∠2+∠3=90°,∴∠1=∠2,∴△ABD∽△CBE.∴=.在Rt△ACB中,∠ACB=30°,tan∠ACB=,∵tan30°=,∴=.又∵∠DBE=90°,∠DEB=30°,∴∠4=60°,∴∠5+∠6=120°.∵△ABD∽△CBE,∴∠5=∠CEB=30°+∠7,![]() ∴∠7=∠5-30°,∠6=120°-∠5,∴∠7+∠6=90°,∴∠DFE=90°即AD⊥CE;(3)在绕点B旋转的过程中,直线AD与EC夹角的度数不改变,且夹角度数为(180-α-β)度
∴∠7=∠5-30°,∠6=120°-∠5,∴∠7+∠6=90°,∴∠DFE=90°即AD⊥CE;(3)在绕点B旋转的过程中,直线AD与EC夹角的度数不改变,且夹角度数为(180-α-β)度
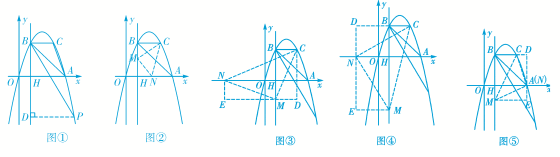
23.(本题14分)如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
(1)求抛物线的表达式,并求出△ABC的面积;
(2)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;
(3)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角![]() 形为等腰直角
形为等腰直角![]() 三角形时,请直接写出此时△CMN的面积.
三角形时,请直接写出此时△CMN的面积.
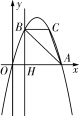
解:(1)把点A(4,0),B(1,3)代入y=ax2+bx,得,解得;∴该抛物线的表达式为y=-x2+4x;∴对称轴为x=2,∴点C的坐标为(3,3),又∵点B的坐标为(1,3),∴BC=2,∴S△ABC=×2×3=3;(2)如图①,过P点作PD⊥BH交BH于点D,设点P(m,-m2+4m),根据题意,得![]() BH=AH=3,HD=m2-4m,PD=m-1,∴S△ABP=S△ABH+S四边形HAPD-S△BPD,即6=×3×3+(3+
BH=AH=3,HD=m2-4m,PD=m-1,∴S△ABP=S△ABH+S四边形HAPD-S△BPD,即6=×3×3+(3+![]() m-1)(m2-4m)-(m-1)(3+m2-4m),∴3m2-15m=0
m-1)(m2-4m)-(m-1)(3+m2-4m),∴3m2-15m=0![]() ,m1=0(舍去),m2=5,∴点P坐标为(5,-5);
,m1=0(舍去),m2=5,∴点P坐标为(5,-5);
(3)以点C、M、N为顶点的三角形为等腰直角三角形时,分三类情况讨论:①以点M为直角顶点且M在x轴上方时,如图②,CM=MN,∠CMN=90°,
则△CBM≌△MHN,∴BC=MH=2,BM=HN=3-2=1,∴M(1,2),N(2,0),由勾股定理得:MC==,∴S△CMN=××=;②以点M为直角顶点且M在x轴下方时,如图③,作辅助线,构建如图③的两直角三角形:Rt△NEM和Rt△MDC,得Rt△NEM≌Rt△MDC,∴EM=CD=5,MD=ME=2,由勾股定理得:CM==,∴S△CMN=××=;③以点N为直角顶点且N在y轴左侧时,如图④,CN=MN,∠MNC=90°,作辅助线,同理得:CN==,∴S△CMN=××=17;④以点N为直角顶点且N在y轴右侧时,作辅助线,如图⑤,同理得:CN===,此时点N与点A重合,∴S![]() △CMN=××=5;⑤以C
△CMN=××=5;⑤以C![]() 为直角顶点时,不能构成满足条件的等腰直角三角形;综上所述:△CMN的面积为:或或17或5
为直角顶点时,不能构成满足条件的等腰直角三角形;综上所述:△CMN的面积为:或或17或5