请选择
请点击全屏查看
2017山东济南中考试题
一、选择题(本大题共15小题,每小题3分,共45分)
1.(2017济南,1,3分)在实数0,-2,,3中,最大的是( )
A.0 B.-2 C. D.3
【答案】D
2.(2017济南,2,3分)如图所示的几何体,它的左视图是( )
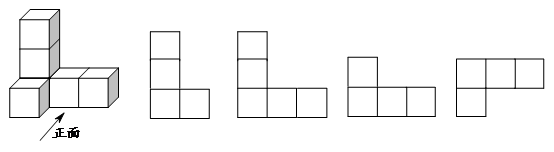 A.B. C.D.
A.B. C.D.
【答案】A
3.(2017济南,3,3分)2017年5月5日国产大型客机C919首飞成功,圆了中国人的“大飞机梦”,它颜值高性能好,全长近39米,最大载客人数168人,最大航程约5550公里.数字5550用科学记数法表示为( )
A.0.555×104 B.5.55×104 C.5.55×103 D.55.5×103
【答案】C
4.(2017济南,4,3分)如图,直线a∥b,直线l与a,b分别相交于A,B两点,AC⊥AB交b于点C,∠1=40°,则∠2的度数是( )
A.40° B.45° C.50° D.60°

【答案】C
5.(2017济南,5,3分)中国古代建筑中的窗格图案美观大方,寓意吉祥,下列绘出的图案中既是轴对称图形又是中心对称图形是( )

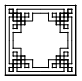
![C:\Users\Administrator.DNISO-20160425G\AppData\Roaming\Tencent\Users\1770413824\QQ\WinTemp\RichOle\2RV26KN2D]Y5ZMILRYGXE58.png](http://img.chusan.com/upLoad/doc2017/y01klev0/090703.005.png)

B.C. D.
【答案】B
6.(2017济南,6,3分)化简÷的结果是( )
A.a2B. C. D.
【答案】D
7.(2017济南,7,3分)关于x的方程x2+5x+m=0的一个根为-2,则另一个根是( )
A.-6 B.-3 C.3 D.6
【答案】B
8.(2017济南,8,3分)《九章算术》是中国传统数学的重要著作,方程术是它的最高成就.其中记载:今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?译文:今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又会差4钱,问人数、物价各是多少?设合伙人数为x人,物价为y钱,以下列出的方程组正确的是( )
A.B.C.D.
【答案】C
9.(2017济南,9,3分)如图,五一旅游黄金周期间,某景区规定A和B为入口,C,D,E为出口,小红随机选一个入口进入景区,游玩后任选一个出口离开,先她选择从A入口进入、从C,D出口离开的概率是( )
A. B. C. D.
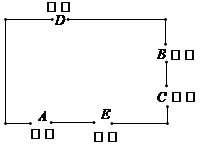
【答案】B
10.(2017济南数学)把直尺、三角尺和圆形螺母按如图所示放置于桌面上,∠CAB=60°,若量出AD=6cm,则圆形螺母的外直径是( )
A.12cm B.24cm C.6cm D.12cm

【答案】C
11.(2017济南,11,3分)将一次函数y=2x的图象向上平移2个单位后,当y>0时,x的取值范围是( )
A.x>-1 B.x>1 C.x>-2 D.x>2
【答案】A
12.(2017济南数学3分)如图,为了测量山坡护坡石坝的坡度(坡面的铅直高度与水平宽度的比称为坡度),把一根长5m的竹竿AC斜靠在石坝旁,量出杆长1m处的D点离地面的高度DE=0.6m,又量的杆底与坝脚的距离AB=3m,则石坝的坡度为( )
A. B.3 C. D.4

【答案】B
13.(2017济南,13,3分)如图,正方形ABCD的对角线AC,BD相较于点O,AB=3,E为OC上一点,OE=1,连接BE,过点A作AF⊥BE于点F,与BD交于点G,则BF的长是( )
A. B.2 C. D.

【答案】A
14.(2017济南,14,3分)二次函数y=ax2+bx+c(a≠0)的图象经过点(-2,0),(x0,0),1<x0<2,与y轴的负半轴相交,且交点在(0,-2)的上方,下列结论:①b>0;②2a<b;③2a-b-1<0;④2a+c<0.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
【答案】C
15.(2017济南数学3分)如图,有一正方形广场ABCD,图形中的线段均表示直行道路,表示一条以A为圆心,以AB为半径的圆弧形道路.如图2,在该广场的A处有一路灯,O是灯泡,夜晚小齐同学沿广场道路散步时,影子长度随行走路线的变化而变化,设他步行的路程为x (m)时,相应影子的长度为y (m),根据他步行的路线得到y与x之间关系的大致图象如图3,则他行走的路线是( )
A.A→B→E→GB.A→E→D→C C.A→E→B→F D.A→B→D→C



【答案】D
二、填空题(本大题共6小题,每小题3分,共18分)
16.(2017济南,16,3分)分解因式:x2-4x+4=__________.
【答案】(x-2)2
17.(2017济南,17,3分)计算:│-2-4│+()0=________________.
【答案】7
18.(2017济南数学)在学校的歌咏比赛中,10名选手的成绩如统计图所示,则这10名选手成绩的众数是_________________.
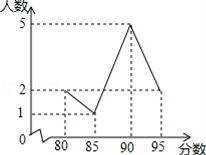
【答案】90
19.(2017济南,19,3分)如图,扇形纸叠扇完全打开后,扇形ABC的面积为300πcm2,∠BAC=120°,BD=2AD,则BD的长度为____________cm.
【答案】20

20.(2017济南数学3分)如图,过点O的直线AB与反比例函数y=的图象交于A,B两点,A(2,1),直线BC∥y轴,与反比例函数y=(x<0)的图象交于点C,连接AC,则△ABC的面积为_________________.

【答案】8
21.(2017济南,21,3分)定义:在平面直角坐标系xOy中,把从点P出发沿综或横方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若P(-1,1),Q(2,3),则P,Q的“实际距离”为5,即PS+SQ=5或PT+TQ=5.环保低碳的共享单车,正式成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为A(3,1),B(5,-3),C(-1,-5),若点M表示单车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标为______________.
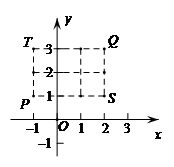
【答案】(1,-2)
三、(2017济南数学)解答题(本大题共7小题,共57分)
22.(2017济南,22,7分)
(1)先化简,再求值:(a+3)2-(a+2)(a+3),其中a=3.
【解】原式=a2+6a+9-(a2+2a+3a+6)
=a2+6a+9-a2-2a-3a-6)
=a+3.
当a=3时,
原式=3+3=6.
(2)解不等式组:
【解】由①,得x≥1.
由②,得x<2.
∴不等式组的解集为:1≤x<2.
23.(2017济南,23,7分)
(1)如图,在矩形ABCD,AD=AE,DF⊥AE于点F.求证:AB=DF.

证明:∵四边形ABCD是矩形,
∴∠B=90°,AD∥BC.
∴∠DAF=∠BEA.
∵DF⊥AE,
∴∠AFD=90°.
∴∠B=∠AFD=90°.
又∵AD=AE,
∴△ADF≌△EBA.
∴AB=DF.
(2)如图,AB是⊙O的直径,∠ACD=25°,求∠BAD的度数.
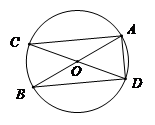
【解】∵AB是⊙O的直径,
∴∠ADB=90°.
∵∠B=∠C=25°,
∴∠BAD=90°-25°=65°.
24.(2017济南,24,8分)
某小区响应济南市提出的“建绿透绿”号召,购买了银杏树和玉兰树共150棵用来美化小区环境,购买银杏树用了12000元,购买玉兰树用了9000元.已知玉兰树的单价是银杏树单价的1.5倍,那么银杏树和玉兰树的单价各是多少?
【解】设银杏树的单价是x元,玉兰树的单价是1.5x元,则
+=150.
解得x=120.
经检验x=120是方程的解.
∴1.5x=180.
答:银杏树的单价是120元,玉兰树的单价是180元,
25.(2017济南,25,8分)
中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本书最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表,如下所示:
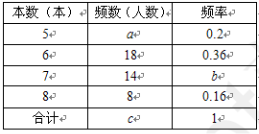

(1)统计表中的a=________,b=___________,c=____________;
(2)请将频数分布表直方图补充完整;
(3)求所有被调查学生课外阅读的平均本数;
(4)若该校八年级共有1200名学生,请你分析该校八年级学生课外阅读7本及以上的人数.
【解】(1)a=10,b=0.28,c=50;
(2)将频数分布表直方图补充完整,如图所示:

(3)所有被调查学生课外阅读的平均本数为:
(5×10+6×18+7×14+8×8)÷50=320÷50=6.4(本).
(4)该校八年级学生课外阅读7本及以上的人数为:
(0.28+0.16)×1200=528(人).
26.(2017济南数学9分)
如图1,□OABC的边OC在y轴的正半轴上,OC=3,A(2,1),反比例函数y=(x>0)的图象经过的B.
(1)求点B的坐标和反比例函数的关系式;
(2)如图2,直线MN分别与x轴、y轴的正半轴交于M,N两点,若点O和点B关于直线MN成轴对称,求线段ON的长;
(3)如图3,将线段OA延长交y=(x>0)的图象于点D,过B,D的直线分别交x轴、y轴于E,F两点,请探究线段ED与BF的数量关系,并说明理由.

【解】(1)过点A作AP⊥x轴于点P,则AP=1,OP=2.
又∵AB=OC=3,
∴B(2,4).
∵反比例函数y=(x>0)的图象经过的B,
∴4=.∴k=8.
∴反比例函数的关系式为y=.


(2)设MN交OB于点H,过点B作BG⊥y轴于点G,则BG=2,OG=4.
∴OB==2.
∵点H是OB的中点,∴点H(1,2).∴OH==.
∵∠OHN=∠OGB=90°,∠HON=∠GOB,
∴△OHN∽△OGB,∴=.∴=.∴ON=2.5.
(3)ED=BF.
(2017济南数学)理由:由点A(2,1)可得直线OA的解析式为y=x.
解方程组,得,.
∵点D在第一象限,∴D(4,2).
由B(2,4),点D(4,2)可得直线BD的解析式为y=-x+6.
把y=0代入上式,得0=-x+6.解得x=6.
∴E(6,0).
∵ED==2,BF==2.
∴ED=BF.
27.(2017济南,27,9分)
某学习小组的学生在学习中遇到了下面的问题:
如图1,在△ABC和△ADE中,∠ACB=∠AED=90°,∠CAB=∠EAD=60°,点E,A,C在同一条直线上,连接BD,点F是BD的中点,连接EF,CF,试判断△CEF的形状并说明理由.
问题探究:
(1)小婷同学提出解题思路:先探究△CEF的两条边是否相等,如EF=CF,以下是她的证明过程
证明:延长线段EF交CB的延长线于点G. ∵F是BD的中点, ∴BF=DF. ∵∠ACB=∠AED=90°, ∴ED∥CG. | ∴∠BGF=∠DEF. 又∵∠BFG=∠DFE, ∴△BGF≌△DEF( ). ∴EF=FG. ∴CF=EF=EG. |
请根据以上证明过程,解答下列两个问题:
①在图1中作出证明中所描述的辅助线;
②在证明的括号中填写理由(请在SAS,ASA,AAS,SSS中选择).
(2)在(1)的探究结论的基础上,请你帮助小婷求出∠CEF的度数,并判断△CEF的形状.
问题拓展:
(3)如图2,当△ADE绕点A逆时针旋转某个角度时,连接CE,延长DE交BC的延长线于点P,其他条件不变,判断△CEF的形状并给出证明.
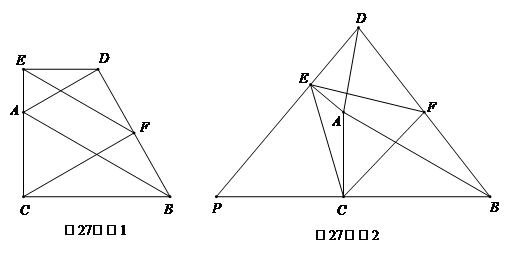
【解】(1)①证明中所叙述的辅助线如下图所示:

②证明的括号中的理由是:AAS.
(2)△CEF是等边三角形.证明如下:
设AE=a,AC=b,则AD=2a,AB=2b,DE=a,BC=b,CE=a+b.
∵△BGF≌△DEF,∴BG=DE=a.∴CG=BC+BG=(a+b).
∵==,=,∴=.
又∵∠ACB=∠ECG,∴△ACE∽△ECG.
∴∠CEF=∠CAB=60°.
又∵CF=EF(已证),
∴△CEF是等边三角形.
(3)△CEF是等边三角形.
证明方法一:
如答案图2,过点B作BN∥DE,交EF的延长线于点N,连接CN,则∠DEF=∠FNB.
又∵DF=BF,∠DFE=∠BFN,∴△DEF≌△BNF.∴BN=DE,EF=FN.
设AC=a,AE=b,则BC=a,DE=b.
∵∠AEP=∠ACP=90°,∴∠P+∠EAC=180°.
∵DP∥BN,∴∠P+∠CBN=180°.∴∠CBN=∠EAC.
在△AEC和△BNC中,
∵===,∠CBN=∠EAC,
∴△AEC∽△BNC.∴∠ECA=∠NCB.∴∠ECN=90°.
又∵EF=FN,
∴CF=EN=EF.
又∵∠CEF=60°,
∴△CEF是等边三角形.


证明方法二:
如答案图3,取AB的中点M,并连接CM,FM,则CM=AB=AC.
又∵∠CAM=60°,∴△ACM是等边三角形.
∴∠ACM=∠AMC=60°.
∵AM=BM,DF=BF,∴MF是△ABD的中位线.∴MF=AD=AE且MF∥AD.
∴∠DAB+∠AMF=180°.
∴∠DAB+∠AMF+∠AMC=180°+60°=240°.
即∠DAB+∠CMF=180°+60°=240°.
又∵∠CAE+∠DAB=360°-∠DAE-∠BAC=360°-60°-60=240°,
∴∠DAB+∠CMF=∠CAE+∠DAB
∴∠CMF=∠CAE.
又∵CM=AC,MF=AE,
∴△CAE≌△CMF.∴CE=CF,∠ECA=∠FCM.
又∵∠ACM=∠ACF+∠FCM=60°,
∴∠ACF+∠ECA=60°.即∠ECF=60°.
又∵CE=CF,
∴△CEF是等边三角形.
28.(2017济南数学9分)
如图1,矩形OABC的顶点A,C的坐标分别为(4,0),(0,6),直线AD交BC于点D,tan∠OAD=2,抛物线M1:y=ax2+bx(a≠0)过A,D两点.
(1)求点D的坐标和抛物线M1的表达式;
(2)点P是抛物线M1对称轴上一动点,当∠CPA=90°时,求所有符合条件的点P的坐标;
(3)如图2,点E(0,4),连接AE,将抛物线M1的图象向下平移m(m>0)个单位得到抛物线M2.
①设点D平移后的对应点为点D′,当点D′恰好在直线AE上时,求m的值;
②当1≤x≤m(m>1)时,若抛物线M2与直线AE有两个交点,求m的取值范围.
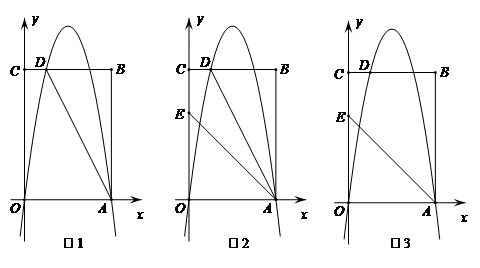
【解】
(1)过点D作DF⊥OA于点F,则DF=6.
∵tan∠OAD==2,∴AF=3.∴OF=1.
∴D(1,6).
把A(4,0),D(1,6)分别代入 y=ax2+bx(a≠0),得
.解得.
∴抛物线M1的表达式为:y=-2x2+8x.


(2)连接AC,则AC==2.
∵y=-2x2+8x=-2(x-2)2+8,
∴抛物线M1的对称轴是直线x=2.
设直线x=2交OA于点N,则N(2,0).
以AC为半径作⊙M,交直线x=2于P1、P2两点,分别连接P1C、P1A、P2C、P2A,则点P1、P2两点就是符合题意的点,且这两点的横坐标都是2.
∵点M是AC的中点,∴点M(2,3).∴MN=2.
∵P1M是Rt△CP1A的斜边上的中线,∴P1M=AC=.
∴P1N=MN+P1M=3+.
∴点P1(2,3+).
同理可得点P2(2,3-).
(3)由A(4,0),点E(0,4)可得直线AE的解析式为y=-x+4.
①点D(1,6)平移后的对应点为点D′(1,6-m),
∵点D′恰好在直线AE上
∴6-m=-1+4.
解得m=3.
∴D′(1,3),m=3.


②如答案图4,作直线x=1,它与直线AE的交点就是点D′(1,3).作直线x=m交直线AE于点Q(m,-m+4).
设抛物线M2的解析式为y=-2x2+8x-m.
若要直线AE与抛物线M2有两个交点N1、N2,则关于x的一元二次方程-2x2+8x-m=-x+4有两个不相等的实数根,
将该方程整理,得2x2+9x+m+4=0.
由△=92-4×2(m+4)>0,
解得m<.
又∵m>1,
∴1<m<…………………………………………………………………………①
∵1≤x≤m(m>1),
∴抛物线M2与直线AE有两个交点N1、N2要在直线x=1与直线x=m所夹的区域内(含左、右边界).
当点N1与点D′(1,3)重合时,把D′(1,3)的坐标代入y=-2x2+8x-m,可得m=3.
∴m≥3…………………………………………………………………………②
当点N2与点Q(m,-m+4)重合时,把点Q(m,-m+4)的坐标代入y=-2x2+8x-m,可得
-m+4=-2m2+8m-m.解得m1=2+,m2=2-(不合题意,舍去).
∴m≥2+…………………………………………………………………………③
由①、②、③可得符合题意的m的取值范围为:
2+≤m<.