请选择
各位同学在查看时请点击全屏查看
2018年吕梁中考数学二次函数专项训练
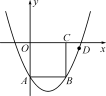
1.如图,在平面直角坐标系xOy中,正方形OABC的边长为2,点A,C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A,B和D(4,-),求抛物线的解析式.
2.如图,二次函数y=ax2+bx+c的图象与x轴交于A,B两点,其中点A(-1,0),点C(0,5),D(1,8)都在抛物线上,M为抛物线的顶点.
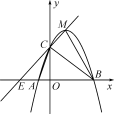
(1)求抛物线的函数解析式;
(2)求直线CM的解析式;
(3)求△MCB的面积.
3.已知一个二次函数,当x=1时,y有最大值8,其图象的形状、开口方向与抛物线y=-2x2相同,则这个二次函数的解析式是( )
A.y=-2x2-x+3 B.y=-2x2+4
C.y=-2x2+4x+8 D.y=-2x2+4x+6
4.已知某二次函数的最大值为2,图象的顶点在直线y=x+1上,并且图象经过点(2,1),求二次函数的解析式.
5.已知二次函数y=ax2+bx+c的x与y的部分对应值如下表:
x | … | -4 | -3 | -2 | -1 | 0 | … |
y | … | -5 | 0 | 3 | 4 | 3 | … |
(1)求此二次函数的解析式;
(2)画出此函数图象;
(3)结合函数图象,当-4<x≤1时,写出y的取值范围.
6.已知一个二次函数的图象经过点A(-1,0),B(3,0)和C(0,-3)三点;
(1)求此二次函数的解析式;
(2)对于实数m,点M(m,-5)是否在这个二次函数的图象上?说明理由.
7.已知抛物线在x轴上截得的线段长是4,对称轴是x=-1,且过点(-2,-6),求该抛物线的解析式.
8.已知y=x2+bx+c的图象向右平移2个单位长度,再向下平移3个单位长度,得到的图象对应的函数解析式为y=x2-2x-3.
(1)b=____,c=____;
(2)求原函数图象的顶点坐标;
(3)求两个图象顶点之间的距离.
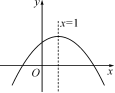
9.如图,已知抛物线y=-x2+bx+c的对称轴为直线x=1,且与x轴的一个交点为(3,0),
那么它对应的函数解析式是 .
10.如图,抛物线与x轴交于A,B两点,与y轴交于C点,点A的坐标为(2,0),点C的坐标为(0,3),它的对称轴是直线x=-.
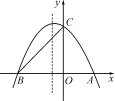
(1)求抛物线的解析式;
(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,
求M点的坐标.
2018年吕梁中考数学二次函数专项训练参考答案
1. 解:y=x2-x-2
2. 解:(1)y=-x2+4x+5
(2)y=-x2+4x+5=-(x-2)2+9,则M点坐标为(2,9),
可求直线MC的解析式为y=2x+5
(3)把y=0代入y=2x+5得2x+5=0,解得x=-,则E点坐标为(-,0),把y=0代入y=-x2+4x+5得-x2+4x+5=0,
解得x1=-1,x2=5,则B点坐标为(5,0),
所以S△MCB=S△MBE-S△CBE=××9-××5=15
3. D
4. 解:∵函数的最大值是2,则此函数顶点的纵坐标是2,又顶点在y=x+1上,那么顶点的横坐标是1,设此函数的解析式是y=a(x-1)2+2,再把(2,1)代入函数中可得a(2-1)2+2=1,解得a=-1,故函数解析式是y=-(x-1)2+2,即y=-x2+2x+1
5. 解:(1)由表知,抛物线的顶点坐标为(-1,4),
设y=a(x+1)2+4,把(0,3)代入得a(0+1)2+4=3,
解得a=-1,∴抛物线的解析式为y=-(x+1)2+4,
即y=-x2-2x+3
(2)图象略
(3)-5<y≤4
6. 解:(1)设二次函数的解析式为y=a(x+1)(x-3),由于抛物线的图象经过C(0,-3),则有-3=a(0+1)(0-3),解得a=1,∴二次函数的解析式为y=(x+1)(x-3),即y=x2-2x-3
(2)由(1)可知y=x2-2x-3=(x-1)2-4,则y的最小值为-4>-5,因此无论m取何值,点M都不在这个二次函数的图象上
7. 解:∵抛物线的对称轴为x=-1,在x轴上截得的线段长为4,∴抛物线与x轴的交点坐标为(-3,0),(1,0),设抛物线解析式为y=a(x+3)(x-1),把(-2,-6)代入得a·(-2+3)·(-2-1)=-6,解得a=2,所以抛物线解析式为y=2(x+3)(x-1),即y=2x2+4x-6
8. (1) 2 0
(2)(-1,-1)
(3)由平移知两个图象顶点之间的距离==
9. y=-x2+2x+3
10. 解:(1)y=-x2-x+3
(2)由y=0得-(x+)2+=0,解得x1=2,x2=-3,
∴B(-3,0).①当CM=BM时,∵BO=CO=3,即△BOC是等腰直角三角形,∴当M点在原点O时,△MBC是等腰三角形,∴M点坐标为(0,0);②当BC=BM时,在Rt△BOC中,BO=CO=3,由勾股定理得BC==3,∴BM=3,∴M点坐标(3-3,0).
综上所述,M点坐标为(3-3,0)或(0,0)
1