请选择
各位同学在查看时请点击全屏查看
2017年黔东南州中考数学试题
一、数学试题选择题(本大题共10小题,每小题4分,共40分)
1.|﹣2|的值是()
A.﹣2 B.2 C.﹣![]() D.
D.![]()
2.如图,∠ACD=120°,∠B=20°,则∠A的度数是()
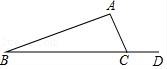
A.120° B.90° C.100° D.30°
3.下列运算结果正确的是()
A.3a﹣a=2 B.(a﹣b)2=a2﹣b2
C.6ab2÷(﹣2ab)=﹣3b D.a(a+b)=a2+b
4.如图所示,所给的三视图表示的几何体是()
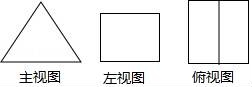
A.圆锥 B.正三棱锥 C.正四棱锥 D.正三棱柱
5.如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=15°,半径为2,则弦CD的长为()

A.2 B.﹣1 C.![]() D.4
D.4
6.已知一元二次方程x2﹣2x﹣1=0的两根分别为x1,x2,则![]() +
+![]() 的值为()
的值为()
A.2 B.﹣1 C.![]() D.﹣2
D.﹣2
7.分式方程![]() =1﹣
=1﹣![]() 的根为()
的根为()
A.﹣1或3 B.﹣1 C.3 D.1或﹣3
8.如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为()
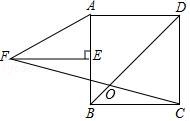
A.60° B.67.5° C.75° D.54°
9.如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:
①b2=4ac;②abc>0;③a>c;④4a﹣2b+c>0,其中正确的个数有()

A.1个 B.2个 C.3个 D.4个
10.我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.

根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为()
A.2017 B.2016 C.191 D.190
二、填空题(本大题共6小题,每小题4分,共24分)
11.在平面直角坐标系中有一点A(﹣2,1),将点A先向右平移3个单位,再向下平移2个单位,则平移后点A的坐标为 .
12.如图,点B、F、C、E在一条直线上,已知FB=CE,AC∥DF,请你添加一个适当的条件 使得△ABC≌△DEF.
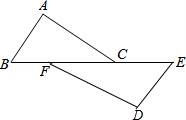
13.在实数范围内因式分解:x5﹣4x= .
14.黔东南下司“蓝每谷”以盛产“优质蓝莓”而吸引来自四面八方的游客,某果农今年的蓝莓得到了丰收,为了了解自家蓝莓的质量,随机从种植园中抽取适量蓝莓进行检测,发现在多次重复的抽取检测中“优质蓝莓”出现的频率逐渐稳定在0.7,该果农今年的蓝莓总产量约为800kg,由此估计该果农今年的“优质蓝莓”产量约是 kg.
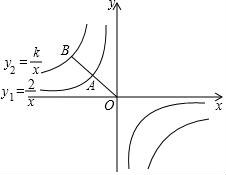
15.如图,已知点A,B分别在反比例函数y1=﹣![]() 和y2=
和y2=![]() 的图象上,若点A是线段OB的中点,则k的值为 .
的图象上,若点A是线段OB的中点,则k的值为 .
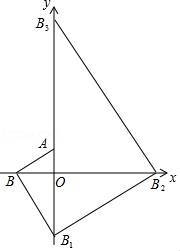
16.把多块大小不同的30°直角三角板如图所示,摆放在平面直角坐标系中,第一块三角板AOB的一条直角边与y轴重合且点A的坐标为(0,1),∠ABO=30°;第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交y轴于点B1;第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交x轴于点B2;第四块三角板的斜边B2B3与第三块三角板的斜边B1B2C垂直且交y轴于点B3;…按此规律继续下去,则点B2017的坐标为 .
三、解答题(本大题共8小题,共86分)
17.计算:﹣1﹣2+|![]() ﹣
﹣![]() |+(π﹣3.14)0﹣tan60°+
|+(π﹣3.14)0﹣tan60°+![]() .
.
18.先化简,再求值:(x﹣1﹣![]() )÷
)÷![]() ,其中x=
,其中x=![]() +1.
+1.
19.解不等式组 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
![]()
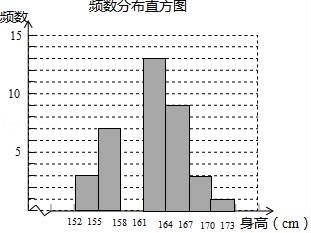
20.某体育老师测量了自己任教的甲、乙两班男生的身高,并制作了如下不完整的统计图表.
身高分组 | 频数 | 频率 |
152≤x<155 | 3 | 0.06 |
155≤x<158 | 7 | 0.14 |
158≤x<161 | m | 0.28 |
161≤x<164 | 13 | n |
164≤x<167 | 9 | 0.18 |
167≤x<170 | 3 | 0.06 |
170≤x<173 | 1 | 0.02 |
根据以上统计图表完成下列问题:
(1)统计表中m= ,n= ,并将频数分布直方图补充完整;
(2)在这次测量中两班男生身高的中位数在: 范围内;
(3)在身高≥167cm的4人中,甲、乙两班各有2人,现从4人中随机推选2人补充到学校国旗护卫队中,请用列表或画树状图的方法求出这两人都来自相同班级的概率.
21.如图,已知直线PT与⊙O相切于点T,直线PO与⊙O相交于A,B两点.
(1)求证:PT2=PA•PB;
(2)若PT=TB=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

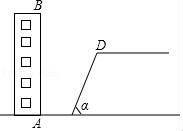
22.如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)
23.某校为了在九月份迎接高一年级的新生,决定将学生公寓楼重新装修,现学校招用了甲、乙两个工程队.若两队合作,8天就可以完成该项工程;若由甲队先单独做3天后,剩余部分由乙队单独做需要18天才能完成.
(1)求甲、乙两队工作效率分别是多少?
(2)甲队每天工资3000元,乙队每天工资1400元,学校要求在12天内将学生公寓楼装修完成,若完成该工程甲队工作m天,乙队工作n天,求学校需支付的总工资w(元)与甲队工作天数m(天)的函数关系式,并求出m的取值范围及w的最小值.
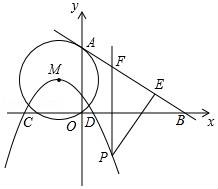
24.如图,⊙M的圆心M(﹣1,2),⊙M经过坐标原点O,与y轴交于点A,经过点A的一条直线l解析式为:y=﹣![]() x+4与x轴交于点B,以M为顶点的抛物线经过x轴上点D(2,0)和点C(﹣4,0).
x+4与x轴交于点B,以M为顶点的抛物线经过x轴上点D(2,0)和点C(﹣4,0).
(1)求抛物线的解析式;
(2)求证:直线l是⊙M的切线;
(3)点P为抛物线上一动点,且PE与直线l垂直,垂足为E,PF∥y轴,交直线l于点F,是否存在这样的点P,使△PEF的面积最小?若存在,请求出此时点P的坐标及△PEF面积的最小值;若不存在,请说明理由.
2017年黔东南中考数学试题参考答案
一、选择题(本大题共10小题,每小题4分,共40分)
1.|﹣2|的值是()
A.﹣2 B.2 C.﹣![]() D.
D.![]()
【考点】15:绝对值.
【分析】根据绝对值的性质作答.
【解答】解:∵﹣2<0,
∴|﹣2|=2.
故选B.
2.如图,∠ACD=120°,∠B=20°,则∠A的度数是()
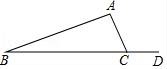
A.120° B.90° C.100° D.30°
【考点】K8:三角形的外角性质.
【分析】根据三角形的外角的性质计算即可.
【解答】解:∠A=∠ACD﹣∠B
=120°﹣20°
=100°,
故选:C.
3.下列运算结果正确的是()
A.3a﹣a=2 B.(a﹣b)2=a2﹣b2
C.6ab2÷(﹣2ab)=﹣3b D.a(a+b)=a2+b
【考点】4I:整式的混合运算.
【分析】各项计算得到结果,即可作出判断.
【解答】解:A、原式=2a,不符合题意;
B、原式=a2﹣2ab+b2,不符合题意;
C、原式=﹣3b,符合题意;
D、原式=a2+ab,不符合题意,
故选C
4.如图所示,所给的三视图表示的几何体是()

A.圆锥 B.正三棱锥 C.正四棱锥 D.正三棱柱
【考点】U3:由三视图判断几何体.
【分析】由左视图和俯视图可得此几何体为柱体,根据主视图是三角形可判断出此几何体为正三棱柱.
【解答】解:∵左视图和俯视图都是长方形,
∴此几何体为柱体,
∵主视图是一个三角形,
∴此几何体为正三棱柱.
故选:D.
5.如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=15°,半径为2,则弦CD的长为()
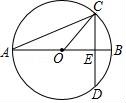
A.2 B.﹣1 C.![]() D.4
D.4
【考点】M5:圆周角定理;KQ:勾股定理;M2:垂径定理.
【分析】根据垂径定理得到CE=DE,∠CEO=90°,根据圆周角定理得到∠COE=30°,根据直角三角形的性质得到CE=![]() OC=1,最后由垂径定理得出结论.
OC=1,最后由垂径定理得出结论.
【解答】解:∵⊙O的直径AB垂直于弦CD,
∴CE=DE,∠CEO=90°,
∵∠A=15°,
∴∠COE=30°,
∵OC=2,
∴CE=![]() OC=1,
OC=1,
∴CD=2OE=2,
故选A.
6.已知一元二次方程x2﹣2x﹣1=0的两根分别为x1,x2,则![]() +
+![]() 的值为()
的值为()
A.2 B.﹣1 C.![]() D.﹣2
D.﹣2
【考点】AB:根与系数的关系.
【分析】根据根与系数的关系得到x1+x2=2,x1x2=﹣1,利用通分得到![]() +
+![]() =
=![]() ,然后利用整体代入的方法计算
,然后利用整体代入的方法计算
【解答】解:根据题意得x1+x2=2,x1x2=﹣1,
所以![]() +
+![]() =
=![]() =
=![]() =﹣2.
=﹣2.
故选D.
7.分式方程![]() =1﹣
=1﹣![]() 的根为()
的根为()
A.﹣1或3 B.﹣1 C.3 D.1或﹣3
【考点】B3:解分式方程.
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
【解答】解:去分母得:3=x2+x﹣3x,
解得:x=﹣1或x=3,
经检验x=﹣1是增根,分式方程的根为x=3,
故选C
8.如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为()
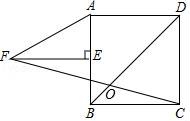
A.60° B.67.5° C.75° D.54°
【考点】LE:正方形的性质.
【分析】如图,连接DF、BF.如图,连接DF、BF.首先证明∠FDB=![]() ∠FAB=30°,再证明△FAD≌△FBC,推出∠ADF=∠FCB=15°,由此即可解决问题.
∠FAB=30°,再证明△FAD≌△FBC,推出∠ADF=∠FCB=15°,由此即可解决问题.
【解答】解:如图,连接DF、BF.
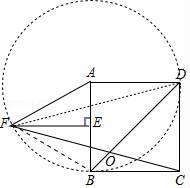
∵FE⊥AB,AE=EB,
∴FA=FB,
∵AF=2AE,
∴AF=AB=FB,
∴△AFB是等边三角形,
∵AF=AD=AB,
∴点A是△DBF的外接圆的圆心,
∴∠FDB=![]() ∠FAB=30°,
∠FAB=30°,
∵四边形ABCD是正方形,
∴AD=BC,∠DAB=∠ABC=90°,∠ADB=∠DBC=45°,
∴∠FAD=∠FBC,
∴△FAD≌△FBC,
∴∠ADF=∠FCB=15°,
∴∠DOC=∠OBC+∠OCB=60°.
故选A.
9.如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:
①b2=4ac;②abc>0;③a>c;④4a﹣2b+c>0,其中正确的个数有()
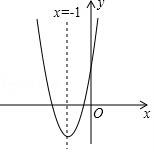
A.1个 B.2个 C.3个 D.4个
【考点】H4:二次函数图象与系数的关系.
【分析】①利用抛物线与x轴有2个交点和判别式的意义对①进行判断;
②由抛物线开口方向得到a>0,由抛物线对称轴位置确定b>0,由抛物线与y轴交点位置得到c>0,则可作判断;
③利用x=﹣1时a﹣b+c<0,然后把b=2a代入可判断;
④利用抛物线的对称性得到x=﹣2和x=0时的函数值相等,即x=﹣2时,y>0,则可进行判断.
【解答】解:①∵抛物线与x轴有2个交点,
∴△=b2﹣4ac>0,
所以①错误;
②∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴在y轴的右侧,
∴a、b同号,
∴b>0,
∵抛物线与y轴交点在x轴上方,
∴c>0,
∴abc>0,
所以②正确;
③∵x=﹣1时,y<0,
即a﹣b+c<0,
∵对称轴为直线x=﹣1,
∴﹣![]() =﹣1,
=﹣1,
∴b=2a,
∴a﹣2a+c<0,即a>c,
所以③正确;
④∵抛物线的对称轴为直线x=﹣1,
∴x=﹣2和x=0时的函数值相等,即x=﹣2时,y>0,
∴4a﹣2b+c>0,
所以④正确.
所以本题正确的有:②③④,三个,
故选C.
10.我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.

根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为()
A.2017 B.2016 C.191 D.190
【考点】4C:完全平方公式.
【分析】根据图形中的规律即可求出(a+b)20的展开式中第三项的系数;
【解答】解:找规律发现(a+b)3的第三项系数为3=1+2;
(a+b)4的第三项系数为6=1+2+3;
(a+b)5的第三项系数为10=1+2+3+4;
不难发现(a+b)n的第三项系数为1+2+3+…+(n﹣2)+(n﹣1),
∴(a+b)20第三项系数为1+2+3+…+20=190,
故选 D.
二、填空题(本大题共6小题,每小题4分,共24分)
11.在平面直角坐标系中有一点A(﹣2,1),将点A先向右平移3个单位,再向下平移2个单位,则平移后点A的坐标为 (1,﹣1) .
【考点】Q3:坐标与图形变化﹣平移.
【分析】根据坐标平移规律即可求出答案.
【解答】解:由题意可知:A的横坐标+3,纵坐标﹣2,即可求出平移后的坐标,
∴平移后A的坐标为(1,﹣1)
故答案为:(1,﹣1)
12.如图,点B、F、C、E在一条直线上,已知FB=CE,AC∥DF,请你添加一个适当的条件 ∠A=∠D 使得△ABC≌△DEF.

【考点】KB:全等三角形的判定.
【分析】根据全等三角形的判定定理填空.
【解答】解:添加∠A=∠D.理由如下:
∵FB=CE,
∴BC=EF.
又∵AC∥DF,
∴∠ACB=∠DFE.
∴在△ABC与△DEF中,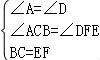 ,
,
∴△ABC≌△DEF(AAS).
故答案是:∠A=∠D.

13.在实数范围内因式分解:x5﹣4x= x(x2+3)(x+![]() )(x﹣
)(x﹣![]() ) .
) .
【考点】58:实数范围内分解因式.
【分析】先提取公因式x,再把4写成22的形式,然后利用平方差公式继续分解因式.
【解答】解:原式=x(x4﹣22),
=x(x2+2)(x2﹣2)
=x(x2+2)(x+![]() )(x﹣
)(x﹣![]() ),
),
故答案是:x(x2+3)(x+![]() )(x﹣
)(x﹣![]() ).
).
14.黔东南下司“蓝每谷”以盛产“优质蓝莓”而吸引来自四面八方的游客,某果农今年的蓝莓得到了丰收,为了了解自家蓝莓的质量,随机从种植园中抽取适量蓝莓进行检测,发现在多次重复的抽取检测中“优质蓝莓”出现的频率逐渐稳定在0.7,该果农今年的蓝莓总产量约为800kg,由此估计该果农今年的“优质蓝莓”产量约是 560 kg.
【考点】X8:利用频率估计概率.
【分析】根据题意可以估计该果农今年的“优质蓝莓”产量.
【解答】解:由题意可得,
该果农今年的“优质蓝莓”产量约是:800×0.7=560kg,
故答案为:560.
15.如图,已知点A,B分别在反比例函数y1=﹣![]() 和y2=
和y2=![]() 的图象上,若点A是线段OB的中点,则k的值为 ﹣8 .
的图象上,若点A是线段OB的中点,则k的值为 ﹣8 .
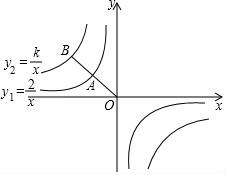
【考点】G6:反比例函数图象上点的坐标特征.
【分析】设A(a,b),则B(2a,2b),将点A、B分别代入所在的双曲线方程进行解答.
【解答】解:设A(a,b),则B(2a,2b),
∵点A在反比例函数y1=﹣![]() 的图象上,
的图象上,
∴ab=﹣2;
∵B点在反比例函数y2=![]() 的图象上,
的图象上,
∴k=2a•2b=4ab=﹣8.
故答案是:﹣8.
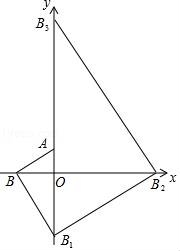
16.把多块大小不同的30°直角三角板如图所示,摆放在平面直角坐标系中,第一块三角板AOB的一条直角边与y轴重合且点A的坐标为(0,1),∠ABO=30°;第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交y轴于点B1;第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交x轴于点B2;第四块三角板的斜边B2B3与第三块三角板的斜边B1B2C垂直且交y轴于点B3;…按此规律继续下去,则点B2017的坐标为 (0,﹣![]() ) .
) .
【考点】D2:规律型:点的坐标.
【分析】根据题意和图象可以发现题目中的变化规律,从而可以求得点B2017的坐标.
【解答】解:由题意可得,
OB=OA•tan60°=1×![]() =
=![]() ,
,
OB1=OB•tan60°=![]() =(
=(![]() )2=3,
)2=3,
OB2=OB1•tan60°=(![]() )3,
)3,
…
∵2017÷4=506…1,
∴点B2017的坐标为(0,﹣![]() ),
),
故答案为:(0,﹣![]() ).
).
三、解答题(本大题共8小题,共86分)
17.计算:﹣1﹣2+|![]() ﹣
﹣![]() |+(π﹣3.14)0﹣tan60°+
|+(π﹣3.14)0﹣tan60°+![]() .
.
【考点】2C:实数的运算;6E:零指数幂;6F:负整数指数幂;T5:特殊角的三角函数值.
【分析】原式利用零指数幂、负整数指数幂法则,特殊角的三角函数值,以及绝对值的代数意义化简,计算即可得到结果.
【解答】解:原式=1+(![]() )+1﹣
)+1﹣![]()
![]()
=2![]()
18.先化简,再求值:(x﹣1﹣![]() )÷
)÷![]() ,其中x=
,其中x=![]() +1.
+1.
【考点】6D:分式的化简求值.
【分析】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
【解答】解:原式=![]() •
•![]() =
=![]() •
•![]() =x﹣1,
=x﹣1,
当x=![]() +1时,原式=
+1时,原式=![]() .
.
19.解不等式组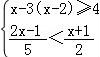 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
![]()
【考点】CB:解一元一次不等式组;C4:在数轴上表示不等式的解集.
【分析】先解不等式组中的每一个不等式,再根据大大取较大,小小取较小,大小小大取中间,大大小小无解,把它们的解集用一条不等式表示出来.
【解答】解:由①得:﹣2x≥﹣2,即x≤1,
由②得:4x﹣2<5x+5,即x>﹣7,
所以﹣7<x≤1.
在数轴上表示为:
![]()
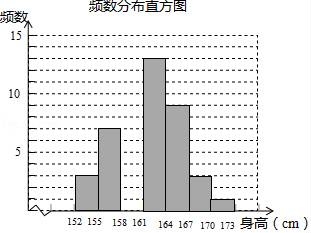
20.某体育老师测量了自己任教的甲、乙两班男生的身高,并制作了如下不完整的统计图表.
身高分组 | 频数 | 频率 |
152≤x<155 | 3 | 0.06 |
155≤x<158 | 7 | 0.14 |
158≤x<161 | m | 0.28 |
161≤x<164 | 13 | n |
164≤x<167 | 9 | 0.18 |
167≤x<170 | 3 | 0.06 |
170≤x<173 | 1 | 0.02 |
根据以上统计图表完成下列问题:
(1)统计表中m= 14 ,n= 0.26 ,并将频数分布直方图补充完整;
(2)在这次测量中两班男生身高的中位数在: 161≤x<164 范围内;
(3)在身高≥167cm的4人中,甲、乙两班各有2人,现从4人中随机推选2人补充到学校国旗护卫队中,请用列表或画树状图的方法求出这两人都来自相同班级的概率.
【考点】X6:列表法与树状图法;V7:频数(率)分布表;V8:频数(率)分布直方图;W4:中位数.
【分析】(1)设总人数为x人,则有![]() =0.06,解得x=50,再根据频率公式求出m,n.画出直方图即可;
=0.06,解得x=50,再根据频率公式求出m,n.画出直方图即可;
(2)根据中位数的定义即可判断;
(3)画出树状图即可解决问题;
【解答】解:(1)设总人数为x人,则有![]() =0.06,解得x=50,
=0.06,解得x=50,
∴m=50×0.28=14,n=![]() =0.26.
=0.26.
故答案为14,0.26.
频数分布直方图:
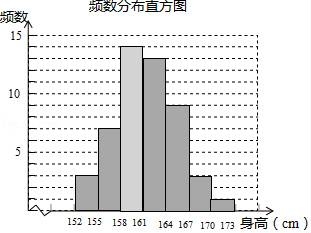
(2)观察表格可知中位数在 161≤x<164内,
故答案为 161≤x<164.
(3)将甲、乙两班的学生分别记为甲1、甲2、乙1、乙2树状图如图所示:
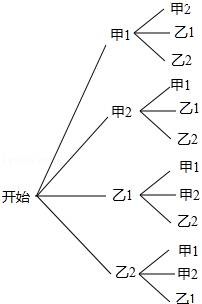
所以P(两学生来自同一所班级)=![]() =
=![]() .
.
21.如图,已知直线PT与⊙O相切于点T,直线PO与⊙O相交于A,B两点.
(1)求证:PT2=PA•PB;
(2)若PT=TB=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

【考点】S9:相似三角形的判定与性质;MC:切线的性质;MO:扇形面积的计算.
【分析】(1)连接OT,只要证明△PTA∽△PBT,可得![]() =
=![]() ,由此即可解决问题;
,由此即可解决问题;
(2)首先证明△AOT是等边三角形,根据S阴=S扇形OAT﹣S△AOT计算即可;
【解答】(1)证明:连接OT.
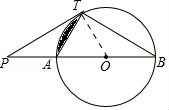
∵PT是⊙O的切线,
∴PT⊥OT,
∴∠PTO=90°,
∴∠PTA+∠OTA=90°,
∵AB是直径,
∴∠ATB=90°,
∴∠TAB+∠B=90°,
∵OT=OA,
∴∠OAT=∠OTA,
∴∠PTA=∠B,∵∠P=∠P,
∴△PTA∽△PBT,
∴![]() =
=![]() ,
,
∴PT2=PA•PB.
(2)∵TP=TB=![]() ,
,
∴∠P=∠B=∠PTA,
∵∠TAB=∠P+∠PTA,
∴∠TAB=2∠B,
∵∠TAB+∠B=90°,
∴∠TAB=60°,∠B=30°,
∴tanB=![]() =
=![]() ,
,
∴AT=1,
∵OA=OT,∠TAO=60°,
∴△AOT是等边三角形,
∴S阴=S扇形OAT﹣S△AOT=![]() ﹣
﹣![]() •12=
•12=![]() ﹣
﹣![]() .
.
22.如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

【考点】T9:解直角三角形的应用﹣坡度坡角问题.
【分析】假设点D移到D′的位置时,恰好∠α=39°,过点D作DE⊥AC于点E,作D′E′⊥AC于点E′,根据锐角三角函数的定义求出DE、CE、CE′的长,进而可得出结论.
【解答】解:假设点D移到D′的位置时,恰好∠α=39°,过点D作DE⊥AC于点E,作D′E′⊥AC于点E′,
∵CD=12米,∠DCE=60°,
∴DE=CD•sin60°=12×![]() =6
=6![]() 米,CE=CD•cos60°=12×
米,CE=CD•cos60°=12×![]() =6米.
=6米.
∵DE⊥AC,D′E′⊥AC,DD′∥CE′,
∴四边形DEE′D′是矩形,
∴DE=D′E′=6![]() 米.
米.
∵∠D′CE′=39°,
∴CE′=![]() ≈
≈![]() ≈12.8,
≈12.8,
∴EE′=CE′﹣CE=12.8﹣6=6.8(米).
答:学校至少要把坡顶D向后水平移动6.8米才能保证教学楼的安全.

23.某校为了在九月份迎接高一年级的新生,决定将学生公寓楼重新装修,现学校招用了甲、乙两个工程队.若两队合作,8天就可以完成该项工程;若由甲队先单独做3天后,剩余部分由乙队单独做需要18天才能完成.
(1)求甲、乙两队工作效率分别是多少?
(2)甲队每天工资3000元,乙队每天工资1400元,学校要求在12天内将学生公寓楼装修完成,若完成该工程甲队工作m天,乙队工作n天,求学校需支付的总工资w(元)与甲队工作天数m(天)的函数关系式,并求出m的取值范围及w的最小值.
【考点】FH:一次函数的应用;B7:分式方程的应用.
【分析】(1)设甲队单独完成需要x天,乙队单独完成需要y天.列出分式方程组即可解决问题;
(2)设乙先工作x天,再与甲合作正好如期完成.则![]() +
+![]() =1,解得x=6.由此可得m的范围,因为乙队每天的费用小于甲队每天的费用,所以让乙先工作6天,再与甲合作6天正好如期完成,此时费用最小;
=1,解得x=6.由此可得m的范围,因为乙队每天的费用小于甲队每天的费用,所以让乙先工作6天,再与甲合作6天正好如期完成,此时费用最小;
【解答】解:(1)设甲队单独完成需要x天,乙队单独完成需要y天.
由题意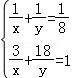 ,解得
,解得![]() ,
,
经检验![]() 是分式方程组的解,
是分式方程组的解,
∴甲、乙两队工作效率分别是![]() 和
和![]() .
.
(2)设乙先工作x天,再与甲合作正好如期完成.
则![]() +
+![]() =1,解得x=6.
=1,解得x=6.
∴甲工作6天,
∵甲12天完成任务,
∴6≤m≤12.
∵乙队每天的费用小于甲队每天的费用,
∴让乙先工作6天,再与甲合作6天正好如期完成,此时费用最小,
∴w的最小值为12×1400+6×3000=34800元.
24.如图,⊙M的圆心M(﹣1,2),⊙M经过坐标原点O,与y轴交于点A,经过点A的一条直线l解析式为:y=﹣![]() x+4与x轴交于点B,以M为顶点的抛物线经过x轴上点D(2,0)和点C(﹣4,0).
x+4与x轴交于点B,以M为顶点的抛物线经过x轴上点D(2,0)和点C(﹣4,0).
(1)求抛物线的解析式;
(2)求证:直线l是⊙M的切线;
(3)点P为抛物线上一动点,且PE与直线l垂直,垂足为E,PF∥y轴,交直线l于点F,是否存在这样的点P,使△PEF的面积最小?若存在,请求出此时点P的坐标及△PEF面积的最小值;若不存在,请说明理由.

【考点】HF:二次函数综合题.
【分析】(1)设抛物线的解析式为y=a(x﹣2)(x+4),将点M的坐标代入可求得a的值,从而得到抛物线的解析式;
(2)连接AM,过点M作MG⊥AD,垂足为G.先求得点A和点B的坐标,可求得,可得到AG、ME、OA、OB的长,然后利用锐角三角函数的定义可证明∠MAG=∠ABD,故此可证明AM⊥AB;
(3))先证明∠FPE=∠FBD.则PF:PE:EF=![]() :2:1.则△PEF的面积=
:2:1.则△PEF的面积=![]() PF2,设点P的坐标为(x,﹣
PF2,设点P的坐标为(x,﹣![]() x2﹣
x2﹣![]() x+
x+![]() ),则F(x,﹣
),则F(x,﹣![]() x+4).然后可得到PF与x的函数关系式,最后利用二次函数的性质求解即可.
x+4).然后可得到PF与x的函数关系式,最后利用二次函数的性质求解即可.
【解答】解:(1)设抛物线的解析式为y=a(x﹣2)(x+4),将点M的坐标代入得:﹣9a=2,解得:a=﹣![]() .
.
∴抛物线的解析式为y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() .
.
(2)连接AM,过点M作MG⊥AD,垂足为G.
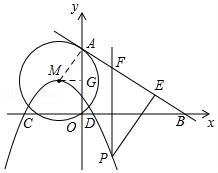
把x=0代入y=﹣![]() x+4得:y=4,
x+4得:y=4,
∴A(0,4).
将y=0代入得:0=﹣![]() x+4,解得x=8,
x+4,解得x=8,
∴B(8,0).
∴OA=4,OB=8.
∵M(﹣1,2),A(0,4),
∴MG=1,AG=2.
∴tan∠MAG=tan∠ABO=![]() .
.
∴∠MAG=∠ABO.
∵∠OAB+∠ABO=90°,
∴∠MAG+∠OAB=90°,即∠MAB=90°.
∴l是⊙M的切线.
(3)∵∠PFE+∠FPE=90°,∠FBD+∠PFE=90°,
∴∠FPE=∠FBD.
∴tan∠FPE=![]() .
.
∴PF:PE:EF=![]() :2:1.
:2:1.
∴△PEF的面积=![]() PE•EF=
PE•EF=![]() ×
×![]() PF•
PF•![]() PF=
PF=![]() PF2.
PF2.
∴当PF最小时,△PEF的面积最小.
设点P的坐标为(x,﹣![]() x2﹣
x2﹣![]() x+
x+![]() ),则F(x,﹣
),则F(x,﹣![]() x+4).
x+4).
∴PF=(﹣![]() x+4)﹣(﹣
x+4)﹣(﹣![]() x2﹣
x2﹣![]() x+
x+![]() )=﹣
)=﹣![]() x+4+
x+4+![]() x2+
x2+![]() x﹣
x﹣![]() =
=![]() x2﹣
x2﹣![]() x+
x+![]() =
=![]() (x﹣
(x﹣![]() )2+
)2+![]() .
.
∴当x=![]() 时,PF有最小值,PF的最小值为
时,PF有最小值,PF的最小值为![]() .
.
∴P(![]() ,
,![]() ).
).
∴△PEF的面积的最小值为=![]() ×(
×(![]() )2=
)2=![]() .
.
第1页(共26页)