请选择
返回
各位同学在查看时请点击全屏查看
2018年铜仁中考数学冲刺试题
题号 | 一 | 二 | 三 | 四 | 总分 |
得分 |
|
|
|
|
|
一、选择题3’*10
1．若双曲线y＝
的图象经过第二、四象限，则k的取值范围是( )
A．k＞0 B．k＜0 C．k≠0 D．不存在
2．已知点A（
）、B（
）是反比例函数
（
）图象上的两点，若
，则有（ ）
A．
B．
C．
D．
3．二次函数y=（x-1）2+2 的最小值是 （ ）
A、2 B、-2 C、-1 D、1
4．井冈山景区为估计该地区国家保护动物穿山甲的只数，先捕捉20只穿山甲给它们分别作上标志，然后放回，待有标志的穿山甲完全回归山林后，第二次捕捉40只穿山甲，发现其中2只有标志。从而估计该地区有穿山甲( )
A．400只 B．600只 C．800只 D．1000只
5．如图，抛物线
的对称轴是直线x=1，且经过点P（3，0），则
的值为（ ）
A、0 B、－1 C、 1 D、 2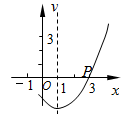 
第5题 第6题
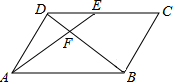
6．如图，在▱ABCD中，E为CD上一点，连接AE、BD，且AE、BD交于点F，S△DEF：S△ABF=4：25，则DE：EC=（ ）
A、2：5 B、2:3 C、3:5 D、3:2
7．在Rt△ABC中，∠C＝90°，若tan A＝
，则sin A等于( )．
A.
B.
C.
D.
8．在相同时刻的物高与影长成比例，如果高为1.5m的测杆的影长为2.5m，那么影长为30m的旗杆的高是（ ）
A．20m B．16m C．18m D．15m
9．方程
的解是（ ）
A．
B．
C．
D．
10．某种药品原价为36元/盒.经过连续两次降价后售价为25元/盒.设平均每次降价的百分率为x，根据题意所列方程正确的是( )
A．36（1－x）2=36－25 B．36 (1－2x) =25
C．36（1－x）2=25 D．36（1－x2）=25
二、填空题3’*8
11．若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根，则实数k的取值范围是
12．若两个连续偶数的积是224，则这两个数的和是__________
13．已知抛物线y=x2+bx+c的部分图象如图所示，若y>0，则x的取值范围是 。
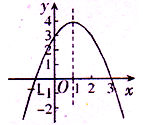
13 15 17
14．函数
的图像是开口向下的抛物线，则
。
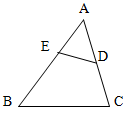
15．如图，已知△ADE∽△ABC，且AD=3，DC=4，AE=2，则BE=________.
16．△ABC中，∠A、∠B都是锐角，若sinA=
，cosB=
，则∠C= ．
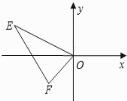
17．已知，直角坐标系中，点E（-4，2），F（-1，-1），以O为位似中心，按比例尺2：1把△EFO缩小，则点E的对应点E′的坐标为 ．
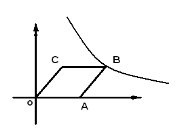
18．如下图，菱形OABC的顶点C的坐标为（3,4），顶点A在x轴的正半轴上，反比例函数y=
（k>0）的图像过顶点B，则k= 。
三、计算题6’*2
19．计算：（π﹣3.14）0+（﹣1）2015+|1﹣
|﹣3tan30°
20．解方程：
四、解答题
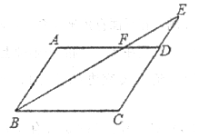21．（10分）如图所示在平行四边形ABCD中，E是CD的延长线上一点，BE与AD交于点F，DE＝
CD.
（1）求证：△ABF∽△CEB；
（2）若S△DEF面积为2，求S平行四边形ABCD的面积。
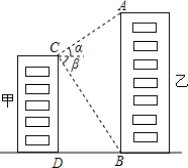
22．（10分）如图，甲、乙两栋高楼的水平距离BD为90米，从甲楼顶部C点测得乙楼顶部A点的仰角α为30°，测得乙楼底部B点的俯角β为60°，求甲、乙两栋高楼各有多高？（计算过程和结果都不取近似值）
23．（10分）某商场销售某品牌童装，平均每天可以售出20件，每件盈利40元，为了扩大销售，增加利润，尽量减少库存，经调查发现，每件童装每降价1元，商场平均可多销售2件，若商场每天想盈利1200元，则童装应降价多少元？
24．（本题满分（10分）分） 为进一步促进青少年科技模型教育的普及和发展，丰富校园科技体育活动，某市6月份将举行中小学科技运动会。下图为某校将参加科技运动会航模比赛（包括空模、海模、车模、建模四个类别）的参赛人数统计图：
（1）该校参加航模比赛的总人数是 人，空模所在扇形的圆心角的度数是 ；
（2）把条形统计图补充完整；
（3）从全市中小学参加航模比赛选手中随机抽取80人，其中有32人获奖．今年该市中小学参加航模比赛人数共2485人，请你估算今年参加航模比赛的获奖人数约是多少人?
25．如图，有长为24米的篱笆，围成中间隔有一道篱笆的长方形的花圃，且花圃的长可借用一段墙体（墙体的最大可用长度a=10米）：如果AB的长为x，面积为y，
（1）求面积y与x的函数关系（写出x的取值范围）（8分）
（2）x取何值时，面积最大？面积最大是多少？（6分）
试卷第3页，总4页
；
．
）；
m时，面积有最大值为46
m2