请选择
2017年江西省萍乡中考数学试题(word版 含答案)
为了方便您的阅读请点击全屏查看
一、选择题(本大题共6个小题,每小题3分,共18分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.﹣6的相反数是()
A.![]() B.﹣
B.﹣![]() C.6 D.﹣6
C.6 D.﹣6
2.在国家“一带一路”战略下,我国与欧洲开通了互利互惠的中欧班列.行程最长,途经城市和国家最多的一趟专列全程长13000km,将13000用科学记数法表示应为()
A.0.13×105 B.1.3×104 C.1.3×105 D.13×103
3.下列图形中,是轴对称图形的是()
A. B.
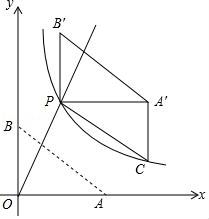
B. C.
C. D.
D.
4.下列运算正确的是()
A.(﹣a5)2=a10 B.2a•3a2=6a2
C.﹣2a+a=﹣3a D.﹣6a6÷2a2=﹣3a3
5.已知一元二次方程2x2﹣5x+1=0的两个根为x1,x2,下列结论正确的是()
A.x1+x2=﹣![]() B.x1•x2=1
B.x1•x2=1
C.x1,x2都是有理数 D.x1,x2都是正数
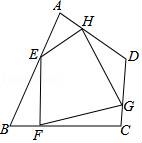
6.如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是()

A.当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形
B.当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形
C.当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形
D.当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形
二、填空题(本大题共6小题,每小题3分,满分18分,将答案填在答题纸上)
7.函数y=![]() 中,自变量x的取值范围是 .
中,自变量x的取值范围是 .
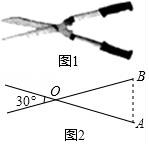
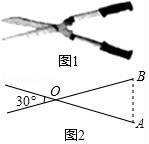
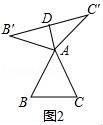
8.如图1是一把园林剪刀,把它抽象为图2,其中OA=OB.若剪刀张开的角为30°,则∠A= 度.
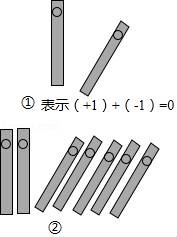
9.中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为 .
10.如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是 .

11.已知一组从小到大排列的数据:2,5,x,y,2x,11的平均数与中位数都是7,则这组数据的众数是 .
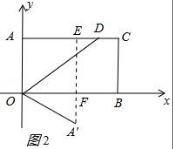
12.已知点A(0,4),B(7,0),C(7,4),连接AC,BC得到矩形AOBC,点D的边AC上,将边OA沿OD折叠,点A的对应边为A'.若点A'到矩形较长两对边的距离之比为1:3,则点A'的坐标为 .
三、解答题(本大题共5小题,每小题6分,共30分.解答应写出文字说明、证明过程或演算步骤.)
13.(1)计算:![]() ÷
÷![]() ;
;
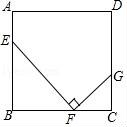
(2)如图,正方形ABCD中,点E,F,G分别在AB,BC,CD上,且∠EFG=90°.求证:△EBF∽△FCG.
14.解不等式组:![]() ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
![]()
15.端午节那天,小贤回家看到桌上有一盘粽子,其中有豆沙粽、肉粽各1个,蜜枣粽2个,这些粽子除馅外无其他差别.
(1)小贤随机地从盘中取出一个粽子,取出的是肉粽的概率是多少?
(2)小贤随机地从盘中取出两个粽子,试用画树状图或列表的方法表示所有可能的结果,并求出小贤取出的两个都是蜜枣粽的概率.
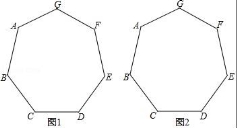
16.如图,已知正七边形ABCDEFG,请仅用无刻度的直尺,分别按下列要求画图.
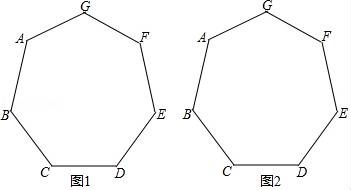
(1)在图1中,画出一个以AB为边的平行四边形;
(2)在图2中,画出一个以AF为边的菱形.
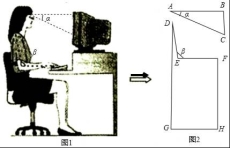
17.如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈![]() ,cos21°≈
,cos21°≈![]() ,tan20°≈
,tan20°≈![]() ,tan43°≈
,tan43°≈![]() ,所有结果精确到个位)
,所有结果精确到个位)

四、(本大题共3小题,每小题8分,共24分).
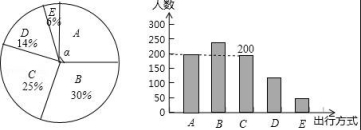
18.为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |

根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
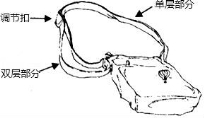
19.如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
单层部分的长度x(cm) | … | 4 | 6 | 8 | 10 | … | 150 |
双层部分的长度y(cm) | … | 73 | 72 | 71 |
| … |
|
(1)根据表中数据的规律,完成以下表格,并直接写出y关于x的函数解析式;
(2)根据小敏的身高和习惯,挎带的长度为120cm时,背起来正合适,请求出此时单层部分的长度;
(3)设挎带的长度为lcm,求l的取值范围.

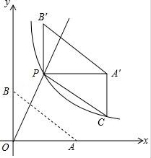
20.如图,直线y=k1x(x≥0)与双曲线y=![]() (x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A'PB'.过点A'作A'C∥y轴交双曲线于点C.
(x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A'PB'.过点A'作A'C∥y轴交双曲线于点C.
(1)求k1与k2的值;
(2)求直线PC的表达式;
(3)直接写出线段AB扫过的面积.
五、(本大题共2小题,每小题9分,共18分).
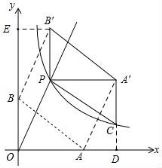
21.如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,过点P作PD⊥OP交⊙O于点D.
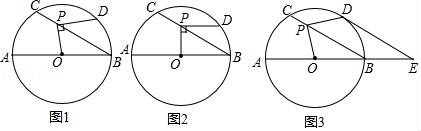
(1)如图2,当PD∥AB时,求PD的长;
(2)如图3,当![]() =
=![]() 时,延长AB至点E,使BE=
时,延长AB至点E,使BE=![]() AB,连接DE.
AB,连接DE.
①求证:DE是⊙O的切线;
②求PC的长.
22.已知抛物线C1:y=ax2﹣4ax﹣5(a>0).
(1)当a=1时,求抛物线与x轴的交点坐标及对称轴;
(2)①试说明无论a为何值,抛物线C1一定经过两个定点,并求出这两个定点的坐标;
②将抛物线C1沿这两个定点所在直线翻折,得到抛物线C2,直接写出C2的表达式;
(3)若(2)中抛物线C2的顶点到x轴的距离为2,求a的值.

六、(本大题共12分)
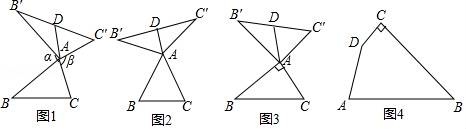
23.我们定义:如图1,在△ABC看,把AB点绕点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
拓展应用
(3)如图4,在四边形ABCD,∠C=90°,∠D=150°,BC=12,CD=2![]() ,DA=6.在四边形内部是否存在点P,使△PDC是△PAB的“旋补三角形”?若存在,给予证明,并求△PAB的“旋补中线”长;若不存在,说明理由.
,DA=6.在四边形内部是否存在点P,使△PDC是△PAB的“旋补三角形”?若存在,给予证明,并求△PAB的“旋补中线”长;若不存在,说明理由.
2017年江西省萍乡中考数学试题参考答案与试题解析
一、选择题(本大题共6个小题,每小题3分,共18分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.﹣6的相反数是()
A.![]() B.﹣
B.﹣![]() C.6 D.﹣6
C.6 D.﹣6
【考点】14:相反数.
【分析】求一个数的相反数,即在这个数的前面加负号.
【解答】解:﹣6的相反数是6,
故选C
2.在国家“一带一路”战略下,我国与欧洲开通了互利互惠的中欧班列.行程最长,途经城市和国家最多的一趟专列全程长13000km,将13000用科学记数法表示应为()
A.0.13×105 B.1.3×104 C.1.3×105 D.13×103
【考点】1I:科学记数法—表示较大的数.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:将13000用科学记数法表示为:1.3×104.
故选B.
3.下列图形中,是轴对称图形的是()
A. B.
B. C.
C. D.
D.
【考点】P3:轴对称图形.
【分析】根据轴对称图形的概念求解.
【解答】解:A、不是轴对称图形,故A不符合题意;
B、不是轴对称图形,故B不符合题意;
C、是轴对称图形,故C符合题意;
D、不是轴对称图形,故D不符合题意;
故选:C.
4.下列运算正确的是()
A.(﹣a5)2=a10 B.2a•3a2=6a2
C.﹣2a+a=﹣3a D.﹣6a6÷2a2=﹣3a3
【考点】4I:整式的混合运算.
【分析】根据整式的运算法则即可求出答案.
【解答】解:(B)原式=6a3,故B错误;
(C)原式=a,故C错误;
(D)原式=﹣3a4,故D错误;
故选(A)
5.已知一元二次方程2x2﹣5x+1=0的两个根为x1,x2,下列结论正确的是()
A.x1+x2=﹣![]() B.x1•x2=1
B.x1•x2=1
C.x1,x2都是有理数 D.x1,x2都是正数
【考点】AB:根与系数的关系.
【分析】先利用根与系数的关系得到x1+x2=![]() >0,x1x2=
>0,x1x2=![]() >0,然后利用有理数的性质可判定两根的符合.
>0,然后利用有理数的性质可判定两根的符合.
【解答】解:根据题意得x1+x2=![]() >0,x1x2=
>0,x1x2=![]() >0,
>0,
所以x1>0,x2>0.
故选D.
6.如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是()
A.当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形
B.当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形
C.当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形
D.当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形
【考点】LN:中点四边形.
【分析】连接四边形各边中点所得的四边形必为平行四边形,根据中点四边形的性质进行判断即可.
【解答】解:A.当E,F,G,H是各边中点,且AC=BD时,EF=FG=GH=HE,故四边形EFGH为菱形,故A正确;
B.当E,F,G,H是各边中点,且AC⊥BD时,∠EFG=∠FGH=∠GHE=90°,故四边形EFGH为矩形,故B正确;
C.当E,F,G,H不是各边中点时,EF∥HG,EF=HG,故四边形EFGH为平行四边形,故C正确;
D.当E,F,G,H不是各边中点时,四边形EFGH可能为菱形,故D错误;
故选:D.
二、填空题(本大题共6小题,每小题3分,满分18分,将答案填在答题纸上)
7.函数y=![]() 中,自变量x的取值范围是 x≥2 .
中,自变量x的取值范围是 x≥2 .
【考点】E4:函数自变量的取值范围.
【分析】根据二次根式的性质,被开方数大于等于0,就可以求解.
【解答】解:依题意,得x﹣2≥0,
解得:x≥2,
故答案为:x≥2.
8.如图1是一把园林剪刀,把它抽象为图2,其中OA=OB.若剪刀张开的角为30°,则∠A= 75 度.
【考点】KH:等腰三角形的性质.
【分析】根据等腰三角形的性质和三角形的内角和即可得到结论.
【解答】解:∵OA=OB,∠AOB=30°,
∴∠A=![]() =75°,
=75°,
故答案为:75.
9.中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为 ﹣3 .

【考点】11:正数和负数.
【分析】根据有理数的加法,可得答案.
【解答】解:图②中表示(+2)+(﹣5)=﹣3,
故答案为:﹣3.
10.如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是 8 .

【考点】U2:简单组合体的三视图;I9:截一个几何体.
【分析】根据从上边看得到的图形是俯视图,可得答案.
【解答】解:从上边看是一个梯形:上底是1,下底是3,两腰是2,
周长是1+2+2+3=8,
故答案为:8.
11.已知一组从小到大排列的数据:2,5,x,y,2x,11的平均数与中位数都是7,则这组数据的众数是 5 .
【考点】W5:众数;W1:算术平均数;W4:中位数.
【分析】根据平均数与中位数的定义可以先求出x,y的值,进而就可以确定这组数据的众数即可.
【解答】解:∵一组从小到大排列的数据:2,5,x,y,2x,11的平均数与中位数都是7,
∴![]() (2+5+x+y+2x+11)=
(2+5+x+y+2x+11)=![]() (x+y)=7,
(x+y)=7,
解得y=9,x=5,
∴这组数据的众数是5.
故答案为5.
12.已知点A(0,4),B(7,0),C(7,4),连接AC,BC得到矩形AOBC,点D的边AC上,将边OA沿OD折叠,点A的对应边为A'.若点A'到矩形较长两对边的距离之比为1:3,则点A'的坐标为 :(![]() ,3)或(
,3)或(![]() ,1)或(2
,1)或(2![]() ,﹣2) .
,﹣2) .
【考点】PB:翻折变换(折叠问题);D5:坐标与图形性质;LB:矩形的性质.
【分析】由已知得出∠A=90°,BC=OA=4,OB=AC=7,分两种情况:(1)当点A'在矩形AOBC的内部时,过A'作OB的垂线交OB于F,交AC于E,当A'E:A'F=1:3时,求出A'E=1,A'F=3,由折叠的性质得:OA'=OA=4,∠OA'D=∠A=90°,在Rt△OA'F中,由勾股定理求出OF=![]() =
=![]() ,即可得出答案;
,即可得出答案;
②当A'E:A'F=3:1时,同理得:A'(![]() ,1);
,1);
(2)当点A'在矩形AOBC的外部时,此时点A'在第四象限,过A'作OB的垂线交OB于F,交AC于E,由A'F:A'E=1:3,则A'F:EF=1:2,求出A'F=![]() EF=
EF=![]() BC=2,在Rt△OA'F中,由勾股定理求出OF=2
BC=2,在Rt△OA'F中,由勾股定理求出OF=2![]() ,即可得出答案.
,即可得出答案.
【解答】解:∵点A(0,4),B(7,0),C(7,4),
∴BC=OA=4,OB=AC=7,
分两种情况:
(1)当点A'在矩形AOBC的内部时,过A'作OB的垂线交OB于F,交AC于E,如图1所示:
①当A'E:A'F=1:3时,
∵A'E+A'F=BC=4,
∴A'E=1,A'F=3,
由折叠的性质得:OA'=OA=4,
在Rt△OA'F中,由勾股定理得:OF=![]() =
=![]() ,
,
∴A'(![]() ,3);
,3);
②当A'E:A'F=3:1时,同理得:A'(![]() ,1);
,1);
(2)当点A'在矩形AOBC的外部时,此时点A'在第四象限,过A'作OB的垂线交OB于F,交AC于E,如图2所示:∵A'F:A'E=1:3,则A'F:EF=1:2,
∴A'F=![]() EF=
EF=![]() BC=2,
BC=2,
由折叠的性质得:OA'=OA=4,
在Rt△OA'F中,由勾股定理得:OF=![]() =2
=2![]() ,
,
∴A'(2![]() ,﹣2);
,﹣2);
故答案为:(![]() ,3)或(
,3)或(![]() ,1)或(2
,1)或(2![]() ,﹣2).
,﹣2).
三、解答题(本大题共5小题,每小题6分,共30分.解答应写出文字说明、证明过程或演算步骤.)
13.(1)计算:![]() ÷
÷![]() ;
;
(2)如图,正方形ABCD中,点E,F,G分别在AB,BC,CD上,且∠EFG=90°.求证:△EBF∽△FCG.

【考点】S8:相似三角形的判定;6A:分式的乘除法;LE:正方形的性质.
【分析】(1)先把分母因式分解,再把除法运算化为乘法运算,然后约分即可;
(2)先根据正方形的性质得∠B=∠C=90°,再利用等角的余角相等得∠BEF=∠CFG,然后根据有两组角对应相等的两个三角形相似可判定△EBF∽△FCG.
【解答】(1)解:原式=![]() •
•![]()
=![]() ;
;
(2)证明:∵四边形ABCD为正方形,
∴∠B=∠C=90°,
∴∠BEF+∠BFE=90°,
∵∠EFG=90°,
∴∠BFE+∠CFG=90°,
∴∠BEF=∠CFG,
∴△EBF∽△FCG.
14.解不等式组:![]() ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
![]()
【考点】CB:解一元一次不等式组;C4:在数轴上表示不等式的解集.
【分析】分别求出每一个不等式的解集,根据解集在数轴上的表示即可确定不等式组的解集.
【解答】解:解不等式﹣2x<6,得:x>﹣3,
解不等式3(x﹣2)≤x﹣4,得:x≤1,
将不等式解集表示在数轴如下:
![]()
则不等式组的解集为﹣3<x≤1
15.端午节那天,小贤回家看到桌上有一盘粽子,其中有豆沙粽、肉粽各1个,蜜枣粽2个,这些粽子除馅外无其他差别.
(1)小贤随机地从盘中取出一个粽子,取出的是肉粽的概率是多少?
(2)小贤随机地从盘中取出两个粽子,试用画树状图或列表的方法表示所有可能的结果,并求出小贤取出的两个都是蜜枣粽的概率.
【考点】X6:列表法与树状图法;X4:概率公式.
【分析】(1)直接利用概率公式求出取出的是肉粽的概率;
(2)直接列举出所有的可能,进而利用概率公式求出答案.
【解答】解:(1)∵有豆沙粽、肉粽各1个,蜜枣粽2个,
∴随机地从盘中取出一个粽子,取出的是肉粽的概率是:![]() ;
;
(2)如图所示:
 ,
,
一共有12种可能,取出的两个都是蜜枣粽的有2种,
故取出的两个都是蜜枣粽的概率为:![]() =
=![]() .
.
16.如图,已知正七边形ABCDEFG,请仅用无刻度的直尺,分别按下列要求画图.
(1)在图1中,画出一个以AB为边的平行四边形;
(2)在图2中,画出一个以AF为边的菱形.
【考点】N3:作图—复杂作图;L5:平行四边形的性质;L8:菱形的性质.
【分析】(1)连接AF、BE、CG,CG交AF于M,交BE于N.四边形ABNM是平行四边形.
(2)连接AF、BE、CG,CG交AF于M,交BE于N,连接DF交BE于H,四边形MNHF是菱形
【解答】解:(1)连接AF、BE、CG,CG交AF于M,交BE于N.四边形ABNM是平行四边形.
(2)连接AF、BE、CG,CG交AF于M,交BE于N,连接DF交BE于H,四边形MNHF是菱形.
17.如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
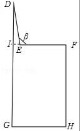
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈![]() ,cos21°≈
,cos21°≈![]() ,tan20°≈
,tan20°≈![]() ,tan43°≈
,tan43°≈![]() ,所有结果精确到个位)
,所有结果精确到个位)
【考点】T8:解直角三角形的应用.
【分析】(1)Rt△ABC中利用三角函数即可直接求解;
(2)延长FE交DG于点I,利用三角函数求得∠DEI即可求得β的值,从而作出判断.
【解答】解:(1)∵Rt△ABC中,tanA=![]() ,
,
∴AB=![]() =
=![]() =
=![]() =55(cm);
=55(cm);
(2)延长FE交DG于点I.
则DI=DG﹣FH=100﹣72=28(cm).
在Rt△DEI中,sin∠DEI=![]() =
=![]() =
=![]() ,
,
∴∠DEI=69°,
∴∠β=180°﹣69°=111°≠100°,
∴此时β不是符合科学要求的100°.
四、(本大题共3小题,每小题8分,共24分).
18.为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |

根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 800 人,其中选择B类的人数有 240 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
【考点】VC:条形统计图;V5:用样本估计总体;VA:统计表;VB:扇形统计图.
【分析】(1)由C类别人数及其百分比可得总人数,总人数乘以B类别百分比即可得;
(2)根据百分比之和为1求得A类别百分比,再乘以360°和总人数可分别求得;
(3)总人数乘以样本中A、B、C三类别百分比之和可得答案.
【解答】解:(1)本次调查的市民有200÷25%=800(人),
∴B类别的人数为800×30%=240(人),
故答案为:800,240;
(2)∵A类人数所占百分比为1﹣(30%+25%+14%+6%)=25%,
∴A类对应扇形圆心角α的度数为360°×25%=90°,A类的人数为800×25%=200(人),
补全条形图如下:
(3)12×(25%+30%+25%)=9.6(万人),
答:估计该市“绿色出行”方式的人数约为9.6万人.
19.如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
单层部分的长度x(cm) | … | 4 | 6 | 8 | 10 | … | 150 |
双层部分的长度y(cm) | … | 73 | 72 | 71 |
| … |
|
(1)根据表中数据的规律,完成以下表格,并直接写出y关于x的函数解析式;
(2)根据小敏的身高和习惯,挎带的长度为120cm时,背起来正合适,请求出此时单层部分的长度;
(3)设挎带的长度为lcm,求l的取值范围.
【考点】FH:一次函数的应用.
【分析】(1)观察表格可知,y是x使得一次函数,设y=kx+b,利用待定系数法即可解决问题;
(2)列出方程组即可解决问题;
(3)由题意当y=0,x=150,当x=0时,y=75,可得75≤l≤150.
【解答】解:(1)观察表格可知,y是x使得一次函数,设y=kx+b,
则有![]() ,解得
,解得![]() ,
,
∴y=﹣![]() x+75.
x+75.
(2)由题意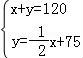 ,解得
,解得![]() ,
,
∴单层部分的长度为90cm.
(3)由题意当y=0,x=150,当x=0时,y=75,
∴75≤l≤150.
20.如图,直线y=k1x(x≥0)与双曲线y=![]() (x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A'PB'.过点A'作A'C∥y轴交双曲线于点C.
(x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A'PB'.过点A'作A'C∥y轴交双曲线于点C.
(1)求k1与k2的值;
(2)求直线PC的表达式;
(3)直接写出线段AB扫过的面积.
【考点】G8:反比例函数与一次函数的交点问题;FA:待定系数法求一次函数解析式;Q3:坐标与图形变化﹣平移.
【分析】(1)把点P(2,4)代入直线y=k1x,把点P(2,4)代入双曲线y=![]() ,可得k1与k2的值;
,可得k1与k2的值;
(2)根据平移的性质,求得C(6,![]() ),再运用待定系数法,即可得到直线PC的表达式;
),再运用待定系数法,即可得到直线PC的表达式;
(3)延长A'C交x轴于D,过B'作B'E⊥y轴于E,根据△AOB≌△A'PB',可得线段AB扫过的面积=平行四边形POBB'的面积+平行四边形AOPA'的面积,据此可得线段AB扫过的面积.
【解答】解:(1)把点P(2,4)代入直线y=k1x,可得4=2k1,
∴k1=2,
把点P(2,4)代入双曲线y=![]() ,可得k2=2×4=8;
,可得k2=2×4=8;
(2)∵A(4,0),B(0,3),
∴AO=4,BO=3,
如图,延长A'C交x轴于D,
由平移可得,A'P=AO=4,
又∵A'C∥y轴,P(2,4),
∴点C的横坐标为2+4=6,
当x=6时,y=![]() =
=![]() ,即C(6,
,即C(6,![]() ),
),
设直线PC的解析式为y=kx+b,
把P(2,4),C(6,![]() )代入可得
)代入可得
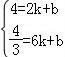 ,解得
,解得![]() ,
,
∴直线PC的表达式为y=﹣![]() x+
x+![]() ;
;
(3)如图,延长A'C交x轴于D,
由平移可得,A'P∥AO,
又∵A'C∥y轴,P(2,4),
∴点A'的纵坐标为4,即A'D=4,
如图,过B'作B'E⊥y轴于E,
∵PB'∥y轴,P(2,4),
∴点B'的横坐标为2,即B'E=2,
又∵△AOB≌△A'PB',
∴线段AB扫过的面积=平行四边形POBB'的面积+平行四边形AOPA'的面积=BO×B'E+AO×A'D=3×2+4×4=22.
五、(本大题共2小题,每小题9分,共18分).
21.如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,过点P作PD⊥OP交⊙O于点D.

(1)如图2,当PD∥AB时,求PD的长;
(2)如图3,当![]() =
=![]() 时,延长AB至点E,使BE=
时,延长AB至点E,使BE=![]() AB,连接DE.
AB,连接DE.
①求证:DE是⊙O的切线;
②求PC的长.
【考点】MR:圆的综合题.
【分析】(1)根据题意首先得出半径长,再利用锐角三角三角函数关系得出OP,PD的长;
(2)①首先得出△OBD是等边三角形,进而得出∠ODE=∠OFB=90°,求出答案即可;
②首先求出CF的长,进而利用直角三角形的性质得出PF的长,进而得出答案.
【解答】解:(1)如图2,连接OD,
∵OP⊥PD,PD∥AB,
∴∠POB=90°,
∵⊙O的直径AB=12,
∴OB=OD=6,
在Rt△POB中,∠ABC=30°,
∴OP=OB•tan30°=6×![]() =2
=2![]() ,
,
在Rt△POD中,
PD=![]() =
=![]() =2
=2![]() ;
;
(2)①证明:如图3,连接OD,交CB于点F,连接BD,
∵![]() =
=![]() ,
,
∴∠DBC=∠ABC=30°,
∴∠ABD=60°,
∵OB=OD,
∴△OBD是等边三角形,
∴OD⊥FB,
∵BE=![]() AB,
AB,
∴OB=BE,
∴BF∥ED,
∴∠ODE=∠OFB=90°,
∴DE是⊙O的切线;
②由①知,OD⊥BC,
∴CF=FB=OB•cos30°=6×![]() =3
=3![]() ,
,
在Rt△POD中,OF=DF,
∴PF=![]() DO=3(直角三角形斜边上的中线,等于斜边的一半),
DO=3(直角三角形斜边上的中线,等于斜边的一半),
∴CP=CF﹣PF=3![]() ﹣3.
﹣3.
22.已知抛物线C1:y=ax2﹣4ax﹣5(a>0).
(1)当a=1时,求抛物线与x轴的交点坐标及对称轴;
(2)①试说明无论a为何值,抛物线C1一定经过两个定点,并求出这两个定点的坐标;
②将抛物线C1沿这两个定点所在直线翻折,得到抛物线C2,直接写出C2的表达式;
(3)若(2)中抛物线C2的顶点到x轴的距离为2,求a的值.
【考点】HA:抛物线与x轴的交点;H6:二次函数图象与几何变换.
【分析】(1)将a=1代入解析式,即可求得抛物线与x轴交点;
(2)①化简抛物线解析式,即可求得两个点定点的横坐标,即可解题;
②根据抛物线翻折理论即可解题;
(3)根据(2)中抛物线C2解析式,分类讨论y=2或﹣2,即可解题;
【解答】解:(1)当a=1时,抛物线解析式为y=x2﹣4x﹣5=(x﹣2)2﹣9,
∴对称轴为y=2;
∴当y=0时,x﹣2=3或﹣3,即x=﹣1或5;
∴抛物线与x轴的交点坐标为(﹣1,0)或(5,0);
(2)①抛物线C1解析式为:y=ax2﹣4ax﹣5,
整理得:y=ax(x﹣4)﹣5;
∵当ax(x﹣4)=0时,y恒定为﹣5;
∴抛物线C1一定经过两个定点(0,﹣5),(4,﹣5);
②这两个点连线为y=﹣5;
将抛物线C1沿y=﹣5翻折,得到抛物线C2,开口方向变了,但是对称轴没变;
∴抛物线C2解析式为:y=﹣ax2+4ax﹣5,
(3)抛物线C2的顶点到x轴的距离为2,
则x=2时,y=2或者﹣2;
当y=2时,2=﹣4a+8a﹣5,解得,a=![]() ;
;
当y=﹣2时,﹣2=﹣4a+8a﹣5,解得,a=![]() ;
;
∴a=![]() 或
或![]() ;
;
六、(本大题共12分)
23.我们定义:如图1,在△ABC看,把AB点绕点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
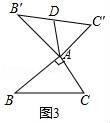
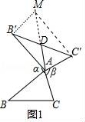
特例感知:
(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= ![]() BC;
BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 4 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
拓展应用
(3)如图4,在四边形ABCD,∠C=90°,∠D=150°,BC=12,CD=2![]() ,DA=6.在四边形内部是否存在点P,使△PDC是△PAB的“旋补三角形”?若存在,给予证明,并求△PAB的“旋补中线”长;若不存在,说明理由.
,DA=6.在四边形内部是否存在点P,使△PDC是△PAB的“旋补三角形”?若存在,给予证明,并求△PAB的“旋补中线”长;若不存在,说明理由.
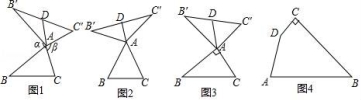
【考点】LO:四边形综合题.
【分析】(1)①首先证明△ADB′是含有30°是直角三角形,可得AD=![]() AB′即可解决问题;
AB′即可解决问题;
②首先证明△BAC≌△B′AC′,根据直角三角形斜边中线定理即可解决问题;
(2)结论:AD=![]() BC.如图1中,延长AD到M,使得AD=DM,连接E′M,C′M,首先证明四边形AC′MB′是平行四边形,再证明△BAC≌△AB′M,即可解决问题;
BC.如图1中,延长AD到M,使得AD=DM,连接E′M,C′M,首先证明四边形AC′MB′是平行四边形,再证明△BAC≌△AB′M,即可解决问题;
(3)存在.如图4中,延长AD交BC的延长线于M,作BE⊥AD于E,作线段BC的垂直平分线交BE于P,交BC于F,连接PA、PD、PC,作△PCD的中线PN.连接DF交PC于O.想办法证明PA=PD,PB=PC,再证明∠APD+∠BPC=180°,即可;
【解答】解:(1)①如图2中,
∵△ABC是等边三角形,
∴AB=BC=AB=AB′=AC′,
∵DB′=DC′,
∴AD⊥B′C′,
∵∠BAC=60°,∠BAC+∠B′AC′=180°,
∴∠B′AC′=120°,
∴∠B′=∠C′=30°,
∴AD=![]() AB′=
AB′=![]() BC,
BC,
故答案为![]() .
.
②如图3中,
∵∠BAC=90°,∠BAC+∠B′AC′=180°,
∴∠B′AC′=∠BAC=90°,
∵AB=AB′,AC=AC′,
∴△BAC≌△B′AC′,
∴BC=B′C′,
∵B′D=DC′,
∴AD=![]() B′C′=
B′C′=![]() BC=4,
BC=4,
故答案为4.
(2)结论:AD=![]() BC.
BC.
理由:如图1中,延长AD到M,使得AD=DM,连接E′M,C′M
∵B′D=DC′,AD=DM,
∴四边形AC′MB′是平行四边形,
∴AC′=B′M=AC,
∵∠BAC+∠B′AC′=180°,∠B′AC′+∠AB′M=180°,
∴∠BAC=∠MB′A,∵AB=AB′,
∴△BAC≌△AB′M,
∴BC=AM,
∴AD=![]() BC.
BC.
(3)存在.
理由:如图4中,延长AD交BC的延长线于M,作BE⊥AD于E,作线段BC的垂直平分线交BE于P,交BC于F,连接PA、PD、PC,作△PCD的中线PN.
连接DF交PC于O.

∵∠ADC=150°,
∴∠MDC=30°,
在Rt△DCM中,∵CD=2![]() ,∠DCM=90°,∠MDC=30°,
,∠DCM=90°,∠MDC=30°,
∴CM=2,DM=4,∠M=60°,
在Rt△BEM中,∵∠BEM=90°,BM=14,∠MBE=30°,
∴EM=![]() BM=7,
BM=7,
∴DE=EM﹣DM=3,
∵AD=6,
∴AE=DE,∵BE⊥AD,
∴PA=PD,PB=PC,
在Rt△CDF中,∵CD=2![]() ,CF=6,
,CF=6,
∴tan∠CDF=![]() ,
,
∴∠CDF=60°=∠CPF,
易证△FCP≌△CFD,
∴CD=PF,∵CD∥PF,
∴四边形CDPF是矩形,
∴∠CDP=90°,
∴∠ADP=∠ADC﹣∠CDP=60°,
∴△ADP是等边三角形,
∴∠ADP=60°,∵∠BPF=∠CPF=60°,
∴∠BPC=120°,
∴∠APD+∠BPC=180°,
∴△PDC是△PAB的“旋补三角形”,
在Rt△PDN中,∵∠PDN=90°,PD=AD=6,DN=![]() ,
,
∴PN=![]() =
=![]() =
=![]() .
.
2017年7月4日