请选择
返回
此试题可能存在乱码情况，在查看时请点击右上角全屏查看
2018年衡阳中考数学冲刺试题
一、选择题（本题共12小题，每题只有一个正确答案，共36分）
1．下列各数中，比﹣1小1的数为（ ）
A．0 B．1 C．﹣2 D．2
2．下列等式成立的是（ ）
A．（a+4）（a﹣4）=a2﹣4 B．2a2﹣3a=﹣a C．a6÷a3=a2 D．（a2）3=a6
3．将数412000用科学记数法表示为（ ）
A．4.12×106 B．4.12×105 C．41.2×104 D．0.412×106
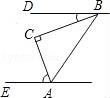
4．如图，在△ABC中，∠C=90°，若BD∥AE，∠DBC=20°，则∠CAE的度数是（ ）
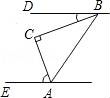
A．40° B．60° C．70° D．80°
5．如图，在一张正六边形纸片中剪下两个全等的直角三角形（阴影部分），拼成一个四边形，若拼成的四边形的面积为2，则纸片的剩余部分拼成的五边形的面积为（ ）
A．5 B．6 C．8 D．10
6．不等式组
的解集在数轴上表示正确的是（ ）
A．
B．
C
D．
7．如图，四边形OABC是矩形，四边形CDEF是正方形，点C，D在x轴的正半轴上，点A在y轴的正半轴上，点F在BC上，点B，E在反比例函数y=
的图象上，OA=2，OC=1，则正方形CDEF的面积为（ ）
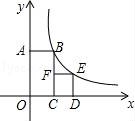
A．4 B．1 C．3 D．2
8．在一个不透明的盒子中装有m个除颜色外完全相同的球，这m个球中只有3个红球，从中随机摸出一个小球，恰好是红球的概率为
，那么m的值是（ ）
A．12 B．15 C．18 D．21
9．某商品原价为180元，连续两次提价x%后售价为300元，下列所列方程正确的是（ ）
A．180（1+x%）=300 B．180（1+x%）2=300 C．180（1﹣x%）=300 D．180（1﹣x%）2=300
10．如图，已知△ABC，按如下步骤作图：
（1）以A圆心，AB长为半径画弧；
（2）以C为圆心，CB长为半径画弧，两弧相交于点D；
（3）连接BD，与AC交于点E，连接AD，CD．
①四边形ABCD是中心对称图形；
②△ABC≌△ADC；
③AC⊥BD且BE=DE；
④BD平分∠ABC．
其中正确的是（ ）
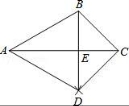
A．①② B．②③ C．①③ D．③④
11．如图，在等边△ABC中，AB=10，BD=4，BE=2，点P从点E出发沿EA方向运动，连接PD，以PD为边，在PD右侧按如图方式作等边△DPF，当点P从点E运动到点A时，点F运动的路径长是（ ）
A．8 B．10 C．3π D．5π
12．如图①，在△ABC中，∠ACB=90°，∠CAB=30°，△ABD是等边三角形．如图②，将四边形ACBD折叠，使D与C重合，EF为折痕，则∠ACE的正弦值为（ ）
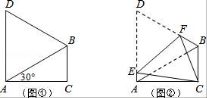
A．
B．
C．
D．
二、填空题（本大题共有6小题，每小题3分，共18分）
13．计算：|﹣5|= ．
14．若分式
有意义，则x的取值范围是 ．
15．因式分解：﹣2x2y+12xy﹣18y= ．
16．已知关于x的一元二次方程（a﹣1）x2﹣2x+1=0有两个不相等的实数根，则a的取值范围是 ．
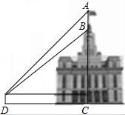
17．如图，某建筑物BC上有一旗杆AB，从与BC相距38m的D处观测旗杆顶部A的仰角为50°，观测旗杆底部B的仰角为45°，则旗杆的高度约为 m．（结果精确到0.1m，参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19）
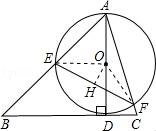
18．如图，△ABC中，∠BAC=60°，∠ABC=45°，AB=
，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB、AC于E、F，连接EF，则线段EF长度的最小值为 ．
三、解答题（共66分）
19．计算：﹣12+（﹣
）﹣2﹣20160+
．
20．先化简，再求值：
，其中x=3．
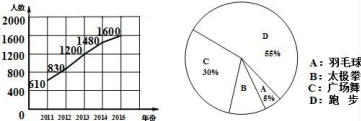
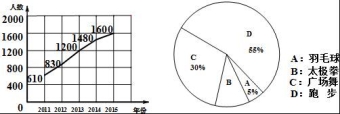
21．某社区从2011年开始，组织全民健身活动，结合社区条件，开展了广场舞、太极拳、羽毛球和跑步四个活动项目，现将参加项目活动总人数进行统计，并绘制成每年参加总人数折线统计图和2015年各活动项目参与人数的扇形统计图，请你根据统计图解答下列题
（1）2015年比2011年增加 人；
（2）请根据扇形统计图求出2015年参与跑步项目的人数；
（3）组织者预计2016年参与人员人数将比2015年的人数增加15%，各活动项目参与人数的百分比与2016年相同，请根据以上统计结果，估计2016年参加太极拳的人数．
22．某市对初二综合素质测评中的审美与艺术进行考核，规定如下：考核综合评价得分由测试成绩（满分100分）和平时成绩（满分100分）两部分组成，其中测试成绩占80%，平时成绩占20%，并且当综合评价得分大于或等于80分时，该生综合评价为A等．
（1）孔明同学的测试成绩和平时成绩两项得分之和为185分，而综合评价得分为91分，则孔明同学测试成绩和平时成绩各得多少分？
（2）某同学测试成绩为70分，他的综合评价得分有可能达到A等吗？为什么？
（3）如果一个同学综合评价要达到A等，他的测试成绩至少要多少分？
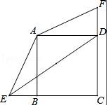
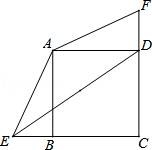
23．已知正方形ABCD中，BC=3，点E、F分别是CB、CD延长线上的点，DF=BE，连接AE、AF，过点A作AH⊥ED于H点．
（1）求证：△ADF≌△ABE；
（2）若BE=1，求tan∠AED的值．
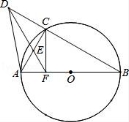
24．已知AB是半径为1的圆O直径，C是圆上一点，D是BC延长线上一点，过点D的直线交AC于E点，且△AEF为等边三角形
（1）求证：△DFB是等腰三角形；
（2）若DA=
AF，求证：CF⊥AB．
25．如图，点A（1，0）、B（4，0）、M（5，3）．动点P从A点出发，沿x轴以每秒1个单位的速度向右移动，过点P的直线l：y=﹣x+b也随之移动．设移动时间为t秒．
（1）当t=1时，求直线l的解析式．
（2）若直线l与线段BM有公共点，求t的取值范围．
（3）当点M关于直线l的对称点落在坐标轴上时，求t的值．
26．如图，抛物线y=ax2+c经过点A（0，2）和点B（﹣1，0）．
（1）求此抛物线的解析式；
（2）将此抛物线平移，使其顶点坐标为（2，1），平移后的抛物线与x轴的两个交点分别为点C，D（点C在点D的左边），求点C，D的坐标；
（3）将此抛物线平移，设其顶点的纵坐标为m，平移后的抛物线与x轴两个交点之间的距离为n，若1＜m＜3，直接写出n的取值范围．
2018年衡阳中考数学冲刺试题参考答案
一、选择题（本题共12小题，每题只有一个正确答案，共36分）
1．下列各数中，比﹣1小1的数为（ ）
A．0 B．1 C．﹣2 D．2
【考点】1A：有理数的减法．
【分析】根据有理数的减法，即可解答．
【解答】解：﹣1﹣1=﹣2，
故选：C．
2．下列等式成立的是（ ）
A．（a+4）（a﹣4）=a2﹣4 B．2a2﹣3a=﹣a C．a6÷a3=a2 D．（a2）3=a6
【考点】4F：平方差公式；35：合并同类项；47：幂的乘方与积的乘方；48：同底数幂的除法．
【分析】A、原式利用平方差公式化简得到结果，即可作出判断；
B、原式不能合并，错误；
C、原式利用同底数幂的除法法则计算得到结果，即可作出判断；
D、原式利用幂的乘方运算法则计算得到结果，即可作出判断．
【解答】解：A、原式=a2﹣16，不成立；
B、原式不能合并，不成立；
C、原式=a3，不成立；
D、原式=a6，成立．
故选D．
3．将数412000用科学记数法表示为（ ）
A．4.12×106 B．4.12×105 C．41.2×104 D．0.412×106
【考点】1I：科学记数法—表示较大的数．
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．
【解答】解：将412000用科学记数法表示为：4.12×105．
故选：B．
4．如图，在△ABC中，∠C=90°，若BD∥AE，∠DBC=20°，则∠CAE的度数是（ ）
A．40° B．60° C．70° D．80°
【考点】JA：平行线的性质．
【分析】过点C作CF∥BD，根据两直线平行，内错角相等即可求解．
【解答】解：过点C作CF∥BD，则CF∥BD∥AE．
∴∠BCF=∠DBC=20°，
∵∠C=90°，
∴∠FCA=90﹣20=70°．
∵CF∥AE，
∴∠CAE=∠FCA=70°．
5．如图，在一张正六边形纸片中剪下两个全等的直角三角形（阴影部分），拼成一个四边形，若拼成的四边形的面积为2，则纸片的剩余部分拼成的五边形的面积为（ ）
A．5 B．6 C．8 D．10
【考点】MM：正多边形和圆．
【分析】由题意得出拼成的四边形的面积是正六边形面积的六分之一，求出正六边形的面积，即可得出结果．
【解答】解：根据题意得：正六边形的面积=6×2=12，
故纸片的剩余部分拼成的五边形的面积=12﹣2=10；
故选：D．
6．不等式组
的解集在数轴上表示正确的是（ ）
A．
B．
C．
D．
【考点】C4：在数轴上表示不等式的解集；CB：解一元一次不等式组．
【分析】首先求不等式组中每个不等式的解集，再利用解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到，找到不等式组的公共解集，再用数轴表示公共部分．
【解答】解：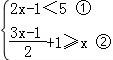
，
由①得：x＜3，
由②得：x≥﹣1，
∴不等式组的解集为：﹣1≤x＜3，
在数轴上表示为：
．
故选：A．
7．如图，四边形OABC是矩形，四边形CDEF是正方形，点C，D在x轴的正半轴上，点A在y轴的正半轴上，点F在BC上，点B，E在反比例函数y=
的图象上，OA=2，OC=1，则正方形CDEF的面积为（ ）
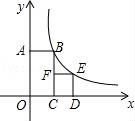
A．4 B．1 C．3 D．2
【考点】G5：反比例函数系数k的几何意义．
【分析】先确定B点坐标（2，1），根据反比例函数图象上点的坐标特征得到k=2，则反比例函数解析式为y=
，设CD=t，则OD=1+t，所以E点坐标为（1+t，t），再根据反比例函数图象上点的坐标特征得（1+t）•t=2，利用因式分解法可求出t的值．
【解答】解：∵OA=2，OC=1，
∴B点坐标为（2，1），
∴k=2×1=2，
∴反比例函数解析式为y=，
设CD=t，则OD=1+t，
∴E点坐标为（1+t，t），
∴（1+t）•t=2，
整理为t2+t﹣2=0，
解得t1=﹣2（舍去），t2=1，
∴正方形ADEF的边长为1．
故选B．
8．在一个不透明的盒子中装有m个除颜色外完全相同的球，这m个球中只有3个红球，从中随机摸出一个小球，恰好是红球的概率为
，那么m的值是（ ）
A．12 B．15 C．18 D．21
【考点】X4：概率公式．
【分析】根据摸到红球的概率为列出方程，求解即可．
【解答】解：由题意得
=
，解得m=15．
故选B．
9．某商品原价为180元，连续两次提价x%后售价为300元，下列所列方程正确的是（ ）
A．180（1+x%）=300 B．180（1+x%）2=300 C．180（1﹣x%）=300 D．180（1﹣x%）2=300
【考点】AC：由实际问题抽象出一元二次方程．
【分析】本题可先用x%表示第一次提价后商品的售价，再根据题意表示第二次提价后的售价，然后根据已知条件得到关于x%的方程．
【解答】解：当商品第一次提价x%时，其售价为180+180x%=180（1+x%）；
当商品第二次提价x%后，其售价为180（1+x%）+180（1+x%）x%=180（1+x%）2．
∴180（1+x%）2=300．
故选B．
10．如图，已知△ABC，按如下步骤作图：
（1）以A圆心，AB长为半径画弧；
（2）以C为圆心，CB长为半径画弧，两弧相交于点D；
（3）连接BD，与AC交于点E，连接AD，CD．
①四边形ABCD是中心对称图形；
②△ABC≌△ADC；
③AC⊥BD且BE=DE；
④BD平分∠ABC．
其中正确的是（ ）
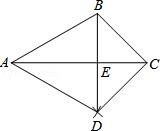
A．①② B．②③ C．①③ D．③④
【考点】N3：作图—复杂作图；KD：全等三角形的判定与性质；R5：中心对称图形．
【分析】利用作法可判断ACAC垂直平分BD，则可对①③进行判断；利用“SSS”可对③进行判断；通过说明∠ABD≠∠CBD可对④进行判断．
【解答】解：由作法得AB=AD，CB=CD，则AC垂直平分BD，点B与点D关于点E对称，而点A与点C不关于E对称，所以①错误，③正确；
利用AB=AC，CD=CB，AC为公共边，所以△ABC≌△ADC，所以②正确；
由于AD与BC不平行，则∠ADB≠∠CBD，而∠ADB=∠ABD，则∠ABD≠∠CBD，所以④错误．
故选B．
11．如图，在等边△ABC中，AB=10，BD=4，BE=2，点P从点E出发沿EA方向运动，连接PD，以PD为边，在PD右侧按如图方式作等边△DPF，当点P从点E运动到点A时，点F运动的路径长是（ ）
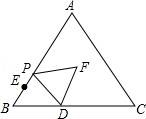
A．8 B．10 C．3π D．5π
【考点】O4：轨迹．
【分析】连结DE，作FH⊥BC于H，如图，根据等边三角形的性质得∠B=60°，过D点作DE′⊥AB，则BE′=
BD=2，则点E′与点E重合，所以∠BDE=30°，DE=
BE=2，接着证明△DPE≌△FDH得到FH=DE=2，于是可判断点F运动的路径为一条线段，此线段到BC的距离为2，当点P在E点时，作等边三角形DEF1，则DF1⊥BC，当点P在A点时，作等边三角形DAF2，作F2Q⊥BC于Q，则△DF2Q≌△ADE，所以DQ=AE=8，所以F1F2=DQ=8，于是得到当点P从点E运动到点A时，点F运动的路径长为8．
【解答】解：连结DE，作FH⊥BC于H，如图，
∵△ABC为等边三角形，
∴∠B=60°，
过D点作DE′⊥AB，则BE′=BD=2，
∴点E′与点E重合，
∴∠BDE=30°，DE=BE=2，
∵△DPF为等边三角形，
∴∠PDF=60°，DP=DF，
∴∠EDP+∠HDF=90°
∵∠HDF+∠DFH=90°，
∴∠EDP=∠DFH，
在△DPE和△FDH中，
，
∴△DPE≌△FDH，
∴FH=DE=2
，
∴点P从点E运动到点A时，点F运动的路径为一条线段，此线段到BC的距离为2，
当点P在E点时，作等边三角形DEF1，∠BDF1=30°+60°=90°，则DF1⊥BC，
当点P在A点时，作等边三角形DAF2，作F2Q⊥BC于Q，则△DF2Q≌△ADE，所以DQ=AE=10﹣2=8，
∴F1F2=DQ=8，
∴当点P从点E运动到点A时，点F运动的路径长为8．
故选：A
12．如图①，在△ABC中，∠ACB=90°，∠CAB=30°，△ABD是等边三角形．如图②，将四边形ACBD折叠，使D与C重合，EF为折痕，则∠ACE的正弦值为（ ）
A．
B．
C．
D．
【考点】PB：翻折变换（折叠问题）．
【分析】在Rt△ABC中，设AB=2a，已知∠ACB=90°，∠CAB=30°，即可求得AB、AC的值，由折叠的性质知：DE=CE，可设出DE、CE的长，然后表示出AE的长，进而可在Rt△AEC中，由勾股定理求得AE、CE的值，即可求∠ACE的正弦值．
【解答】解：∵△ABC中，∠ACB=90°，∠BAC=30°，设AB=2a，
∴AC=a，BC=a；
∵△ABD是等边三角形，
∴AD=AB=2a；
设DE=EC=x，则AE=2a﹣x；
在Rt△AEC中，由勾股定理，得：（2a﹣x）2+3a2=x2，解得x=
；
∴AE=
，EC=，
∴sin∠ACE=
=．
故选：B．
二、填空题（本大题共有6小题，每小题3分，共18分）
13．计算：|﹣5|= 5 ．
【考点】15：绝对值．
【分析】根据绝对值定义去掉这个绝对值的符号即可．
【解答】解：|﹣5|=5．
故答案为：5
14．若分式
有意义，则x的取值范围是 x≠3 ．
【考点】62：分式有意义的条件．
【分析】根据分式有意义，分母不等于0列式计算即可得解．
【解答】解：由题意得，x﹣3≠0，
解得，x≠3．
故答案为：x≠3．
15．因式分解：﹣2x2y+12xy﹣18y= ﹣2y（x﹣3）2 ．
【考点】55：提公因式法与公式法的综合运用．
【分析】原式提取公因式，再利用完全平方公式分解即可．
【解答】解：原式=﹣2y（x2﹣6x+9）
=﹣2y（x﹣3）2．
故答案为：﹣2y（x﹣3）2．
16．已知关于x的一元二次方程（a﹣1）x2﹣2x+1=0有两个不相等的实数根，则a的取值范围是 a＜2，且a≠1 ．
【考点】AA：根的判别式；A1：一元二次方程的定义．
【分析】本题是根的判别式的应用，因为关于x的一元二次方程（a﹣1）x2﹣2x+l=0有两个不相等的实数根，所以△=b2﹣4ac＞0，从而可以列出关于a的不等式，求解即可，还要考虑二次项的系数不能为0．
【解答】解：∵关于x的一元二次方程（a﹣1）x2﹣2x+l=0有两个不相等的实数根，
∴△=b2﹣4ac＞0，即4﹣4×（a﹣1）×1＞0，
解这个不等式得，a＜2，
又∵二次项系数是（a﹣1），
∴a≠1．
故a的取值范围是a＜2且a≠1．
17．如图，某建筑物BC上有一旗杆AB，从与BC相距38m的D处观测旗杆顶部A的仰角为50°，观测旗杆底部B的仰角为45°，则旗杆的高度约为 7.2 m．（结果精确到0.1m，参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19）
【考点】TA：解直角三角形的应用﹣仰角俯角问题．
【分析】根据题意分别在两个直角三角形中求得AF和BF的长后求差即可得到旗杆的高度．
【解答】解：根据题意得：EF⊥AC，CD∥FE，
∴四边形CDEF是矩形，
已知底部B的仰角为45°即∠BEF=45°，
∴∠EBF=45°，
∴CD=EF=FB=38，
在Rt△AEF中，
AF=EF•tan50°=38×1.19≈45.22
∴AB=AF﹣BF=45.22﹣38≈7.2，
∴旗杆的高约为7.2米．
故答案为：7.2．
18．如图，△ABC中，∠BAC=60°，∠ABC=45°，AB=
，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB、AC于E、F，连接EF，则线段EF长度的最小值为 
．
【考点】M2：垂径定理；J4：垂线段最短；KQ：勾股定理．
【分析】由垂线段的性质可知，当AD为△ABC的边BC上的高时，直径最短，如图，连接OE，OF，过O点作OH⊥EF，垂足为H，由Rt△ADB为等腰直角三角形，则AD=BD=1，即此时圆的直径为1，再根据圆周角定理可得到∠EOH=60°，则在Rt△EOH中，利用锐角三角函数可计算出EH=
，然后根据垂径定理即可得到EF=2EH=
．
【解答】解：由垂线段的性质可知，当AD为△ABC的边BC上的高时，直径最短，
如图，连接OE，OF，过O点作OH⊥EF，垂足为H，
在Rt△ADB中，∠ABC=45°，AB=
，
∴AD=BD=1，即此时圆的直径为1，
∵∠EOF=2∠BAC=120°，
而∠EOH=∠EOF，
∴∠EOH=60°，
在Rt△EOH中，EH=OE•sin∠EOH=
•sin60°=，
∵OH⊥EF，
∴EH=FH，
∴EF=2EH=，
即线段EF长度的最小值为．
故答案为．
三、解答题（共66分）
19．计算：﹣12+（﹣）﹣2﹣20160+
．
【考点】2C：实数的运算；6E：零指数幂；6F：负整数指数幂．
【分析】直接利用负整数指数幂的性质以及零指数幂的性质和立方根的性质分别化简各数，进而得出答案．
【解答】解：﹣12+（﹣）﹣2﹣20160+
=﹣1+4﹣1﹣3
=﹣1．
20．先化简，再求值：
，其中x=3．
【考点】6D：分式的化简求值．
【分析】首先通分计算括号里面的，再计算乘法，把多项式分解因式后约分，得出化简结果，再代入x的值计算即可．
【解答】解：
=
•
=
，
当x=3时，原式=
=
．
21．某社区从2011年开始，组织全民健身活动，结合社区条件，开展了广场舞、太极拳、羽毛球和跑步四个活动项目，现将参加项目活动总人数进行统计，并绘制成每年参加总人数折线统计图和2015年各活动项目参与人数的扇形统计图，请你根据统计图解答下列题
（1）2015年比2011年增加 990 人；
（2）请根据扇形统计图求出2015年参与跑步项目的人数；
（3）组织者预计2016年参与人员人数将比2015年的人数增加15%，各活动项目参与人数的百分比与2016年相同，请根据以上统计结果，估计2016年参加太极拳的人数．
【考点】VD：折线统计图；V5：用样本估计总体；VB：扇形统计图．
【分析】（1）用2015年的人数﹣2011年的人数即可；
（2）用2015年总人数×参与跑步项目的人数所占的百分数即可；
（3）2015年总人数×（1+15%）×参加太极拳的人数所占的百分数即可．
【解答】解：（1）1600﹣610=990（人）；
故答案为：990人；
（2）1600×55%=880（人）；
答：2015年参与跑步项目的人数为880人；
（3）1600×（1+15%）×（1﹣55%﹣30%﹣5%）=184（人）；
答：估计2016年参加太极拳的人数为184人．
22．某市对初二综合素质测评中的审美与艺术进行考核，规定如下：考核综合评价得分由测试成绩（满分100分）和平时成绩（满分100分）两部分组成，其中测试成绩占80%，平时成绩占20%，并且当综合评价得分大于或等于80分时，该生综合评价为A等．
（1）孔明同学的测试成绩和平时成绩两项得分之和为185分，而综合评价得分为91分，则孔明同学测试成绩和平时成绩各得多少分？
（2）某同学测试成绩为70分，他的综合评价得分有可能达到A等吗？为什么？
（3）如果一个同学综合评价要达到A等，他的测试成绩至少要多少分？
【考点】C9：一元一次不等式的应用；9A：二元一次方程组的应用．
【分析】（1）分别利用孔明同学的测试成绩和平时成绩两项得分之和为185分，而综合评价得分为91分，分别得出等式求出答案；
（2）利用测试成绩占80%，平时成绩占20%，进而得出答案；
（3）首先假设平时成绩为满分，进而得出不等式，求出测试成绩的最小值．
【解答】解：（1）设孔明同学测试成绩为x分，平时成绩为y分，依题意得：
解之得：
答：孔明同学测试成绩为90分，平时成绩为95分；
（2）由题意可得：80﹣70×80%=24，
24÷20%=120＞100，故不可能．
（3）设平时成绩为满分，即100分，综合成绩为100×20%=20，
设测试成绩为a分，根据题意可得：20+80%a≥80，
解得：a≥75
答：他的测试成绩应该至少为75分．
23．已知正方形ABCD中，BC=3，点E、F分别是CB、CD延长线上的点，DF=BE，连接AE、AF，过点A作AH⊥ED于H点．
（1）求证：△ADF≌△ABE；
（2）若BE=1，求tan∠AED的值．
【考点】LE：正方形的性质；KD：全等三角形的判定与性质．
【分析】（1）根据辅助线的性质得到AD=AB，∠ADC=∠ABC=90°，由邻补角的定义得到∠ADF=∠ABE=90°，于是得到结论；
（2）过点A作AH⊥DE于点H，根据勾股定理得到AE=
，ED=
=5，根据三角形的面积S△AED=AD×BA=
，S△ADE=ED×AH=，求得AH=1.8，由三角函数的定义即可得到结论．
【解答】解：（1）正方形ABCD中，
∵AD=AB，∠ADC=∠ABC=90°，
∴∠ADF=∠ABE=90°，
在△ADF与△ABE中，
，
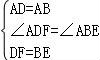∴△ADF≌△ABE；
（2）过点A作AH⊥DE于点H，
在Rt△ABE中，∵AB=BC=3，
∵BE=1，
∴AE=，ED=
=5，
∵S△AED=
AD×BA=
，
S△ADE=ED×AH=，
解出AH=1.8，
在Rt△AHE中，EH=2.6，
∴tan∠AED=
．
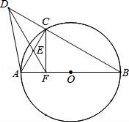
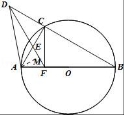
24．已知AB是半径为1的圆O直径，C是圆上一点，D是BC延长线上一点，过点D的直线交AC于E点，且△AEF为等边三角形
（1）求证：△DFB是等腰三角形；
（2）若DA=AF，求证：CF⊥AB．
【考点】M5：圆周角定理；KJ：等腰三角形的判定与性质；KO：含30度角的直角三角形．
【分析】（1）由AB是⊙O直径，得到∠ACB=90°，由于△AEF为等边三角形，得到∠CAB=∠EFA=60°，根据三角形的外角的性质即可得到结论；
（2）过点A作AM⊥DF于点M，设AF=2a，根据等边三角形的性质得到FM=EM=a，AM=
a，在根据已知条件得到AB=AF+BF=8a，根据直角三角形的性质得到AE=EF=AF=CE=2a，推出∠ECF=∠EFC，根据三角形的内角和即可得到结论．
【解答】解：（1）∵AB是⊙O直径，
∴∠ACB=90°，
∵△AEF为等边三角形，
∴∠CAB=∠EFA=60°
∴∠B=30°，
∵∠EFA=∠B+∠FDB，
∴∠B=∠FDB=30°，
∴△DFB是等腰三角形；
（2）过点A作AM⊥DF于点M，设AF=2a，
∵△AEF是等边三角形，∴FM=EM=a，AM=a，
在Rt△DAM中，AD=AF=2a，AM=
，
∴DM=5a，∴DF=BF=6a，
∴AB=AF+BF=8a，
在Rt△ABC中，∠B=30°，∠ACB=90°，∴AC=4a，
∵AE=EF=AF=2a，
∴CE=AC﹣AE=2a，
∴∠ECF=∠EFC，
∵∠AEF=∠ECF+∠EFC=60°，∴∠CFE=30°，
∴∠AFC=∠AFE+∠EFC=60°+30°=90°，
∴CF⊥AB．
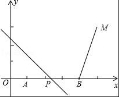
25．如图，点A（1，0）、B（4，0）、M（5，3）．动点P从A点出发，沿x轴以每秒1个单位的速度向右移动，过点P的直线l：y=﹣x+b也随之移动．设移动时间为t秒．
（1）当t=1时，求直线l的解析式．
（2）若直线l与线段BM有公共点，求t的取值范围．
（3）当点M关于直线l的对称点落在坐标轴上时，求t的值．
【考点】FI：一次函数综合题．
【分析】（1）根据点P的运动用t表示出点P的坐标，代入t=1即可得出点P的坐标，根据点P的坐标利用待定系数法即可求出此时直线l的解析式；
（2）分别找出直线l过点B、M时的b值，再根据一次函数图象上点的坐标特征找出t值，由此即可得出结论；
（3）分对称点落在x轴和y轴上考虑．根据直线l的解析式可设出直线MC的解析式，根据点M的坐标利用待定系数法即可求出直线MC的解析式，则直线MC与x、y轴的交点将是点M关于直线l的对称点，找出两直线的交点坐标，再根据一次函数图象上点的坐标特征求出t值即可得出结论．
【解答】解：（1）直线y=﹣x+b交x轴于点P（1+t，0）（b＞0，t≥0）．
当t=1时，1+t=2，
∴P（2，0），
∴﹣2+b=0，
解得b=2，
故当t=1时，直线l的解析式为y=﹣x+2．
（2）当直线y=﹣x+b过点B（4，0）时，有1+t=4，
∴t=3；
当直线y=﹣x+b过点M（5，3）时，有3=﹣5+b，
解得：b=8，
∴0=﹣（1+t）+8，
解得t=7．
故若l与线段BM有公共点，t的取值范围是：3≤t≤7．
（3）点M关于直线l的对称点落在对称轴上分两种情况（如图所示）：
①当点M的对称点落在y轴上时，过点M作MC⊥直线l，交y轴于点C，交直线l于点D，则点C为点M在坐标轴上的对称点．
设直线MC的解析式为y=x+m，则：3=5+m，解得：m=﹣2，
∴直线MC的解析式为y=x﹣2．
当x=0时，y=0﹣2=﹣2，
∴C点坐标为（0，﹣2）．
∵（0+5）÷2=2.5，（3﹣2）÷2=0.5，
∴D点坐标为（2.5，0.5），
当直线y=﹣x+b过点D（2.5，0.5）时，有0.5=﹣2.5+b，解得：b=3，
即0=﹣（1+t）+3，解得t=2．
∴t为2时，点M关于l的对称点落在y轴上．
②当点M的对称点落在x轴上时，设直线MC分别与x轴、直线l交与点E，F．
当y=0时，有x﹣2=0，解得：x=2，
∴点E（2，0），点F（3.5，1.5）．
∴1.5=﹣3.5+b，解得：b=5，
∴t=b﹣1=4，
∴t=4时点M关于l的对称点落在x轴上．
综上，t=2或4时，M的对称点在坐标轴上．
26．如图，抛物线y=ax2+c经过点A（0，2）和点B（﹣1，0）．
（1）求此抛物线的解析式；
（2）将此抛物线平移，使其顶点坐标为（2，1），平移后的抛物线与x轴的两个交点分别为点C，D（点C在点D的左边），求点C，D的坐标；
（3）将此抛物线平移，设其顶点的纵坐标为m，平移后的抛物线与x轴两个交点之间的距离为n，若1＜m＜3，直接写出n的取值范围．
【考点】H6：二次函数图象与几何变换；H8：待定系数法求二次函数解析式．
【分析】（1）把点A、B的坐标分别代入函数解析式，列出关于a、c的方程组，通过解方程求得它们的值；
（2）根据平移的规律写出平移后抛物线的解析式，然后令y=0，则解关于x的方程，即可求得点C、D的横坐标；
（3）根据根与系数的关系来求n的取值范围；
【解答】解：（1）∵抛物线y=ax2+c经过点A（0，2）和点B（﹣1，0）．
∴
解得：
∴此抛物线的解析式为y=﹣2x2+2；
（2）∵此抛物线平移后顶点坐标为（2，1），
∴抛物线的解析式为y=﹣2（x﹣2）2+1
令y=0，即﹣2（x﹣2）2+1=0
解得 x1=2+
，x2=2﹣．
∵点C在点D的左边
∴C（ 2﹣，0），D（2+，0）‘
（3）
＜n＜
．
第1页（共28页）