请选择
此试题可能存在乱码情况,在查看时请点击右上角全屏查看
2018年毕节中考数学模拟试题
(50分钟,共100分)
班级:_______ 姓名:_______ 得分:_______ 发展性评语:_____________
一、请准确填空(每小题3分,共24分)
1.化简![]() =______.
=______.
2.据生物学统计,一个健康的成年女子体内每毫升血液中红细胞的数量约为420万个,用科学记数法可表示为______.
3.请你写出函数y=2(x-1)2+1与y=x2具有的一个共同性质______.
4.如图1,请写出等腰梯形ABCD(AB∥CD)特有而一般梯形不具有的特征(至少三个)
.
5.如图2,是小明制作的一个圆锥形纸帽的示意图,围成这个纸帽的纸的面积为______ cm2.(π取3.14)
6.小刚的爸爸是养鱼专业户,他想对自己鱼池中的鱼的总质量进行评估,第一次捞出100条,称得质量为268 kg,将每条鱼做出记号放入水中,待它们充分混入鱼群后,又捞出200条,称得质量为545 kg,且带有记号的鱼有5条,其鱼池中估计有鱼_____条,总质量为_____kg.
7.如图3,ABCD中,E、F分别是对角线AC上的点,只添加一个条件______,就可确定△ADE≌△CBF.
8.水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图4,是一个正方体的平面展开图,若图中的“才”表示正方体的前面,“拼”表示正方体的左面,“会”表示上面,则“勇”“搏”“赢”分别表示正方体的______.


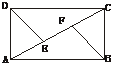

图1 图2 图3 图4
二、相信你的选择(每小题3分,共24分)
9 .计算(-2a2)3÷a3-a3的结果是
A.-8a5 B.-8a6 C.-9a3 D.-8a2-a3
10.如图5,天平右盘中的每个砝码的质量都是0.5 g,则物体x的质量G(g)的取值范围在数轴上可表示为
![]()
图5

图6
11.点P在平面直角坐标系中第一象限内,且又是半径为1的⊙O上的点,已知∠POx=α,则点P关于y轴对称的点P′的坐标为
A.(sinα,cosα) B.(cosα,sinα)
C.(-sinα,cosα) D.(-cosα,sinα)
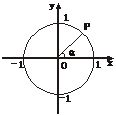
图7
12.已知小红同学身高1.5米,经太阳光照射,在地面的影长为2米,若此时测得一楼房在同一地面的影长为60米,则楼高应为
A.40米 B.45米 C.80米 D.90米
13.有一大捆粗细均匀的电线,现要确定其长度,先称出这捆电线的总质量为a kg,从中截取2 m长的电线,称出它的质量为b kg,那么这捆电线的总长度为
A.![]() m B.
m B.![]() m C.
m C.![]() m D.(
m D.(![]() -2) m
-2) m
14.函数y=![]() 中,自变量x的取值范围是
中,自变量x的取值范围是
A.x≠2 B.x≥2 C.x>2 D.x<2
15.图8是跷跷板图,横板AB绕点O上下转动,立柱OC与水平地面垂直,当横板AB的A端着地时,测得∠OAC=28°,则在玩跷跷板时,上下最大可以转动的角度为
A.28° B.56° C.62° D.84°
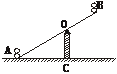
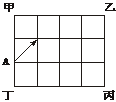
图8 图9
16.图9是一个长方形屋地平面图,其与地面垂直的四周墙上挂的全是平面镜(每一墙上为一整体镜面),在点A处有一直线光束沿所示方向射出,经平面镜反射后(多次反射)最终会射入哪个墙角(不计光线粗度,图中为等格小正方形)
A.甲 B.乙 C.丙 D.丁
三、考查你的基本功(共19分)
17.(5分)先将![]() ·(1+
·(1+![]() )化简,然后请你选一个合理的值,求原式的值.
)化简,然后请你选一个合理的值,求原式的值.
18.(6分)如图10,在10×5的正方形网中,每个小正方形的边长均为单位1,将△ABC向右平移4个单位,得到△A′B′C′,再把△A′B′C′绕点A′逆时针旋转90°,得到△A″B″C″,请你画出△A′B′C′和△A″B″C″(不要求写画法).
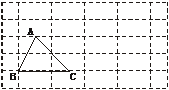
图10
19.(8分)如图11是电动模型车的轨道示意图,其中∠ACB=90°,轨道BC的垂直平分线是DF交BC于D,交AB于E,F在DE上,并且AF=CE,当甲乙两辆电动模型车同时以相同的速度从F站出发,甲车的行驶路线是F→E→B→D,乙车的行驶路线是F→A→C→D,点D为终点站,假设两辆车在行驶过程中除行驶路线不同外,其余各方面均相同,请你推测一番.甲、乙两车能否同时到D点终点站.说明你推测的理由.

图11
四、生活中的数学(共18分)
20.(8分)2005年,某校三个年级的初中在校学生共有796名,学生的出生月份统计如下,根据图中数据回答下列问题:

图12
(1)出生人数超过60人的月份有哪些?
(2)出生人数最多的是几月?
(3)在这些学生中至少有两人生日在10月5日是不可能或可能,还是必然的?
(4)如果你随机地遇到这些学生中的一位,那么这位学生生日在哪一个月的概率最小?
21.(10分)根据图13中提供的信息,请你提出合理的问题,并加以解答.

图13
五、探究拓展与应用(共15分)
22.(10分)如图14二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A.
(1)根据图象请你确定a、b、c的符号,并说明理由;
(2)如果点A的坐标为(0,-3),∠ABC=45° ,∠ACB=60°,求这个二次函数的表达式.
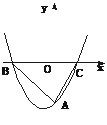

图14 图15
23.(5分)小颖的妈妈做了一个矩形枕套,又在枕套四周镶了一圈矩形花边,如图15所示.妈妈说内外矩形相似,小颖说不一定,你同意谁的说法,还是另有见解?小颖说的“不一定”有什么含义?说明你的理由.(注:花边的宽度相等)
参考答案
一、1.1-![]() 2.4.2×106 3.都过点(1,1)
2.4.2×106 3.都过点(1,1)
4.AD=BC;∠D=∠C,∠A=∠B;对角线相等,是轴对称图形
5.3140 6.4000 10840
7.DE∥BF或DE=BF或AE=CF……
8.后面、下面、右面
二、9.C 10.B 11.D 12.B 13.C 14.C 15.B 16.A
三、17.解:![]()
取x=5 , ∴x-5=0.
18.(略)
19.甲乙两车能同时到达点D终点站
∵DE垂直平分BC , ∴EB=EC,D为BC中点,ED⊥BC .
∴AC⊥BC . ∴AC∥ED . ∴E为AB中点. ∴AE=EC=EB.
又∵AF=AE , ∴∠F=∠FEA=∠BED .
∵∠BED=∠BAC, ∴∠F=∠FEA=∠BAC=∠ACE.
∴△AFE≌△EAC . ∴EF=AC .∴FE+EB+BD=FA+AC+EC .
四、20.(1)1月份、2月份、3月份、7月份、8月份、9月份、10月份、11月份、12月份.
(2)1月份.
(3)可能的(∵![]() >2) . (4)5月份.
>2) . (4)5月份.
21.问:甲、乙两件服装成本各多少元?
解:设甲、乙两件服装的成本分别x元、y元.
由题意得![]()
即![]() 解得
解得![]()
答:甲、乙两件服装的成本分别为300元、200元.
五、22.解:(1)抛物线开口向上,∴a>0.
对称轴x=-![]() 在y轴左侧, ∴-
在y轴左侧, ∴-![]() <0 . ∵a>0, ∴b>0.
<0 . ∵a>0, ∴b>0.
抛物线与y轴的交点A在y轴负半轴上, ∴c<0.
(2)∵A(0,-3), ∴OA=3, ∠ABC=45°. ∴OB=OA=3. ∴B(-3,0)
∵∠ACO=60°,在Rt△AOC中,tan60°=![]() ,
,
∴OC=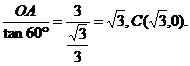
设二次函数表达式为y=ax2+bx+c,
∴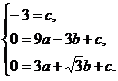 得
得
∴表达式为![]()
23.小颖的说法有一定道理.
因为长、宽不相等的矩形,各边延长相等的长度,得到的矩形始终与原矩形不相似.
只有长、宽相等即为正方形,各边延长相等的长度得到的“矩形”与“原矩形”才相似.