请选择
返回
2017年威海市中考数学试题
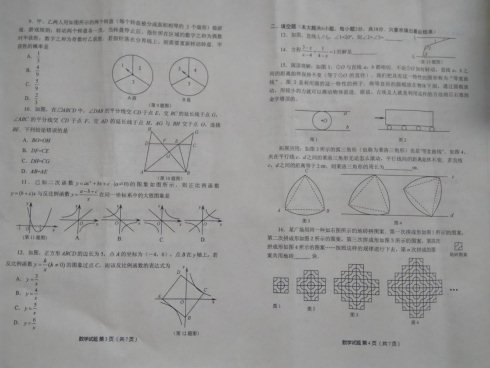
一、2017年威海市中考数学试题选择题：
1.从新华网获悉：商务部5月27日发布的数据显示，一季度，中国与“一带一路”沿线国家在经贸合作领域保持良好发展势头，双边货物贸易总额超过16553亿元人民币.16553亿用科学记数法表示为（ ）
A．
B．
C．
D．
2.某校排球队10名队员的身高（厘米）如下：
195,186,182，188,182,186,188，186,188.
这组数据的众数和中位数分别是（ ）
A．186,188 B．188,187 C．187,188 D．188,186
3.下列运算正确的是（ ）
A．
B．
C．
D．
4.计算
的结果是（ ）
A．1 B．2 C．
D．3
5.不等式组
的解集在数轴上表示正确的是（ ）
6.为了方便行人推车过某天桥，市政府在
高的天桥一侧修建了
长的斜道（如图所示）.我们可以借助科学计算器求这条斜道倾斜角的度数.具体按键顺序是（ ）
7.若
是方程
的一个根，则
的值为（ ）
A．
B．
C.
D．
8.一个几何体由
个大小相同的小正方体搭成，其左视图、俯视图如图所示，则
的最小值是（ ）
A．5 B．7 C. 9 D．10
9.甲、乙两人用如图所示的两个转盘（每个转盘被分成面积相等的3个扇形）做游戏.游戏规则：转动两个转盘各一次，当转盘停止后，指针所在区域的数字之和为偶数时甲获胜；数字之和为奇数时乙获胜.若指针落在分界线上，则需要重新转动转盘.甲获胜的概率是（ ）
A．
B．
C.
D．
10.如图，在□
中，
的平分线交
于点
，交
的延长线于点
，
的平分线交
于点
，交
的延长线于点
，
与
交于点
，连接
.下列结论错误的是（ ）
A．
B．
C.
D．
11.已知二次函数
的图象如图所示，则正比例函6570
与反比例函数
在同一坐标系中的大致图象是（ ）
12.如图，正方形
的边长为5，点
的坐标为
，点
在
轴上，若反比例函数
（
）的图象过点
，则该反比例函数的表达式为（ ）
A．
B．
C. 
D．
二、2017年威海市中考数学试题填空题
13.如图，直线
，
，则
．
14.方程
的解是 ．
15.阅读理解：如图1，⊙
与直线
都相切.不论⊙
如何转动，直线
之间的距离始终保持不变（等于⊙
的半径）.我们把具有这一特性的图形称为“等宽曲线”.图2是利用圆的这一特性的例子.将等直径的圆棍放在物体下面，通过圆棍滚动，用较小的力就可以推动物体前进.据说，古埃及就是利用只有的方法将巨石推到金字塔顶的.
拓展应用：如图3所示的弧三角形（也称为莱洛三角形）也是“等宽曲线”.如图4，夹在平行线
之间的莱洛三角形无论怎么滚动，平行线间的距离始终不变.若直线
之间的距离等于
，则莱洛三角形的周长为 
.
16.某广场用同一种如图所示的地砖拼图案.第一次拼成形如图1所示的图案，第二次拼成形如图2所示的图案，第三次拼成形如图3的图案，第四次拼成形如图4的图案……按照只有的规律进行下去，第
次拼成的图案用地砖 块.
17.如图，
点的坐标为
，
点的坐标为
，
点的坐标为
，
点的坐标为
.小明发现：线段
与线段
存在一种特殊关系，即其中一条线段绕着某点旋转一个角度可以得到另一线段.你认为这个旋转中心的坐标是 .
18.如图，
为等边三角形，
，若
为
内一动点，且满足
，则线段
长度的最小值为 .
三、2017年威海市中考数学试题解答题
用圆规、直尺作图，不写作法，但要保留作图痕迹
19.先化简
，然后从
的范围内选取一个合适的整数作为
的值代入求值.
20.某农场去年计划生产玉米和小麦共200吨.采用新技术后，实际产量为225吨，其中玉米超产5%，小麦超产15%.该农场去年实际生产玉米、小麦各多少吨？
21.央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求，欲购进一批学生喜欢的图书.学校组织学生会成随机抽取部分学生进行问卷调查，被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类.根据调查结果绘制了统计图（未完成）.请根据图中信息，解答下列问题：
（1）此次共调查了 名学生；
（2）将条形统计图补充完整；
（3）图2中“小说类”所在扇形的圆心角为 度；
（4）若该学校共有学生2500人，估计该校喜欢“社科类”书籍的学生人数.
22.图1是太阳能热水器装置的示意图.利用玻璃吸热管可以把太阳能转化为热能.玻璃吸热管与太阳光线垂直时，吸收太阳能的效果最好.假设某用户要求根据本地区冬至正午时刻太阳光线与地面水平线的夹角（
）确定玻璃吸热管的倾斜角（太阳光线与玻璃吸热管垂直），前完成以下计算.
如图2，
，垂足为点
，
，垂足为点
，
，
，
，
，垂足为点
.
（1）若
，则
的长约为 
；
（参考数据：
）
（2）若
，
，求
的长.
23.已知：
为⊙
的直径，
，弦
，直线
与
相交于点
，弦
在⊙
上运动且保持长度不变，⊙
的切线
交
于点
.
（1）如图1，若
，求证：
；
（2）如图2，当点
运动至与点
重合时，试判断
与
是否相等，并说明理由.
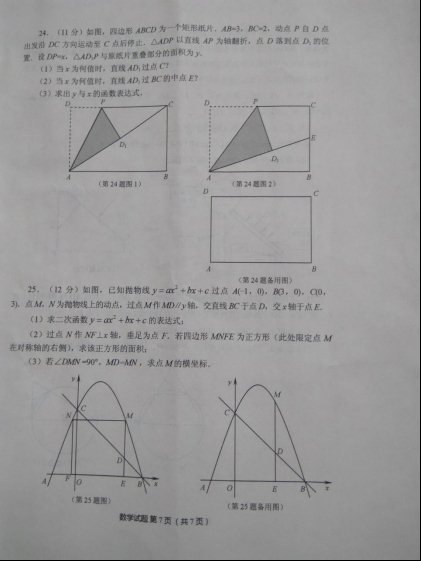
24.如图，四边形
为一个矩形纸片，
，
，动点
自
点出发沿
方向运动至
点后停止.
以直线
为轴翻折，点
落到点
的位置.设
，
与原纸片重叠部分的面积为
.
（1）当
为何值时，直线
过点
？
（2）当
为何值时，直线
过
的中点
？
（3）求出
与
的函数关系式.
25.如图，已知抛物线
过点
，
，
.点
为抛物线上的动点，过点
作
轴，交直线
于点
，交
轴于点
.
（1）求二次函数的表达式；
（2）过点
作
轴，垂足为点
.若四边形
为正方形（此处限定点
在对称轴的右侧），求该正方形的面积；
（3）若
，
，求点
的横坐标.
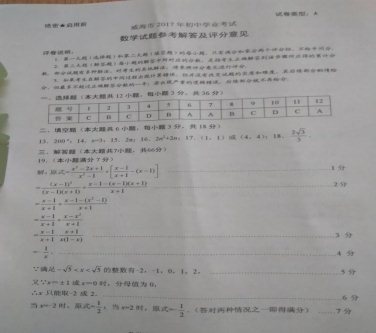
2017年威海市中考数学试题答案解析
