请选择
2017年广东省深圳市中考数学试题【精编解析版】
由于版式的问题,试题可能会出现乱码的现象,为了方便您的阅读请点击全屏查看
一、选择题
1.﹣2的绝对值是()
A.﹣2 B.2 C.﹣![]() D.
D.![]()
2.图中立体图形的主视图是()

A. B.
B. C.
C. D.
D.![]()
3.随着“一带一路”建设的不断发展,我国已与多个国家建立了经贸合作关系,去年中哈铁路(中国至哈萨克斯坦)运输量达8200000吨,将8200000用科学记数法表示为()
A.8.2×105 B.82×105 C.8.2×106 D.82×107
4.观察下列图形,其中既是轴对称又是中心对称图形的是()
A. B.
B. C.
C. D.
D.
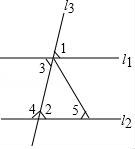
5.下列选项中,哪个不可以得到l1∥l2?()
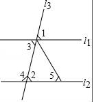
A.∠1=∠2 B.∠2=∠3 C.∠3=∠5 D.∠3+∠4=180°
6.不等式组![]() 的解集为()
的解集为()
A.x>﹣1 B.x<3 C.x<﹣1或x>3 D.﹣1<x<3
7.一球鞋厂,现打折促销卖出330双球鞋,比上个月多卖10%,设上个月卖出x双,列出方程()
A.10%x=330 B.(1﹣10%)x=330 C.(1﹣10%)2x=330 D.(1+10%)x=330
8.如图,已知线段AB,分别以A、B为圆心,大于![]() AB为半径作弧,连接弧的交点得到直线l,在直线l上取一点C,使得∠CAB=25°,延长AC至M,求∠BCM的度数为()
AB为半径作弧,连接弧的交点得到直线l,在直线l上取一点C,使得∠CAB=25°,延长AC至M,求∠BCM的度数为()

A.40° B.50° C.60° D.70°
9.下列哪一个是假命题()
A.五边形外角和为360°
B.切线垂直于经过切点的半径
C.(3,﹣2)关于y轴的对称点为(﹣3,2)
D.抛物线y=x2﹣4x+2017对称轴为直线x=2
10.某共享单车前a公里1元,超过a公里的,每公里2元,若要使使用该共享单车50%的人只花1元钱,a应该要取什么数()
A.平均数 B.中位数 C.众数 D.方差
11.如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10cm,则树AB的高度是()m.
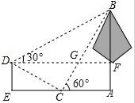
A.20![]() B.30 C.30
B.30 C.30![]() D.40
D.40
12.如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OE•OP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=![]() ,其中正确结论的个数是()
,其中正确结论的个数是()
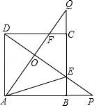
A.1 B.2 C.3 D.4
二、填空题
13.因式分解:a3﹣4a= .
14.在一个不透明的袋子里,有2个黑球和1个白球,除了颜色外全部相同,任意摸两个球,摸到1黑1白的概率是 .
15.阅读理解:引入新数i,新数i满足分配律,结合律,交换律,已知i2=﹣1,那么(1+i)•(1﹣i)= .
16.如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,Rt△MPN,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP= .

三、解答题
17.计算:|![]() ﹣2|﹣2cos45°+(﹣1)﹣2+
﹣2|﹣2cos45°+(﹣1)﹣2+![]() .
.
18.先化简,再求值:(![]() +
+![]() )÷
)÷![]() ,其中x=﹣1.
,其中x=﹣1.
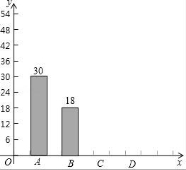
19.深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.
类型 | 频数 | 频率 |
A | 30 | x |
B | 18 | 0.15 |
C | m | 0.40 |
D | n | y |
(1)学生共 人,x= ,y= ;
(2)补全条形统计图;
(3)若该校共有2000人,骑共享单车的有 人.
20.一个矩形周长为56厘米.
(1)当矩形面积为180平方厘米时,长宽分别为多少?
(2)能围成面积为200平方米的矩形吗?请说明理由.
21.如图,一次函数y=kx+b与反比例函数y=![]() (x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(1)直接写出一次函数y=kx+b的表达式和反比例函数y=![]() (x>0)的表达式;
(x>0)的表达式;
(2)求证:AD=BC.

22.如图,线段AB是⊙O的直径,弦CD⊥AB于点H,点M是![]() 上任意一点,AH=2,CH=4.
上任意一点,AH=2,CH=4.
(1)求⊙O的半径r的长度;
(2)求sin∠CMD;
(3)直线BM交直线CD于点E,直线MH交⊙O于点N,连接BN交CE于点F,求HE•HF的值.

23.如图,抛物线y=ax2+bx+2经过点A(﹣1,0),B(4,0),交y轴于点C;
(1)求抛物线的解析式(用一般式表示);
(2)点D为y轴右侧抛物线上一点,是否存在点D使S△ABC=![]() S△ABD?若存在请直接给出点D坐标;若不存在请说明理由;
S△ABD?若存在请直接给出点D坐标;若不存在请说明理由;
(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长.

2017年广东省深圳市中考数学试题参考答案与试题解析
一、选择题
1.﹣2的绝对值是()
A.﹣2 B.2 C.﹣![]() D.
D.![]()
【考点】15:绝对值.
【分析】根据绝对值的定义,可直接得出﹣2的绝对值.
【解答】解:|﹣2|=2.
故选B.
2.图中立体图形的主视图是()

A. B.
B. C.
C. D.
D.![]()
【考点】U2:简单组合体的三视图.
【分析】根据主视图是从正面看的图形解答.
【解答】解:从正面看,共有两层,下面三个小正方体,上面有一个小正方体,在中间.
故选A.
3.随着“一带一路”建设的不断发展,我国已与多个国家建立了经贸合作关系,去年中哈铁路(中国至哈萨克斯坦)运输量达8200000吨,将8200000用科学记数法表示为()
A.8.2×105 B.82×105 C.8.2×106 D.82×107
【考点】1I:科学记数法—表示较大的数.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:将8200000用科学记数法表示为:8.2×106.
故选:C.
4.观察下列图形,其中既是轴对称又是中心对称图形的是()
A. B.
B. C.
C. D.
D.
【考点】R5:中心对称图形;P3:轴对称图形.
【分析】根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形,以及轴对称图形的定义即可判断出.
【解答】解:A、是中心对称图形,不是轴对称图形,选项不符合题意;
B、是轴对称图形,不是中心对称图形,选项不符合题意;
C、是中心对称图形,不是轴对称图形,选项不符合题意;
D、是中心对称图形,也是轴对称图形,选项符合题意.
故选D.
5.下列选项中,哪个不可以得到l1∥l2?()
A.∠1=∠2 B.∠2=∠3 C.∠3=∠5 D.∠3+∠4=180°
【考点】J9:平行线的判定.
【分析】分别根据平行线的判定定理对各选项进行逐一判断即可.
【解答】解:A、∵∠1=∠2,∴l1∥l2,故本选项错误;
B、∵∠2=∠3,∴l1∥l2,故本选项错误;
C、∠3=∠5不能判定l1∥l2,故本选项正确;
D、∵∠3+∠4=180°,∴l1∥l2,故本选项错误.
故选C.
6.不等式组![]() 的解集为()
的解集为()
A.x>﹣1 B.x<3 C.x<﹣1或x>3 D.﹣1<x<3
【考点】CB:解一元一次不等式组.
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【解答】解:解不等式3﹣2x<5,得:x>﹣1,
解不等式x﹣2<1,得:x<3,
∴不等式组的解集为﹣1<x<3,
故选:D.
7.一球鞋厂,现打折促销卖出330双球鞋,比上个月多卖10%,设上个月卖出x双,列出方程()
A.10%x=330 B.(1﹣10%)x=330 C.(1﹣10%)2x=330 D.(1+10%)x=330
【考点】89:由实际问题抽象出一元一次方程.
【分析】设上个月卖出x双,等量关系是:上个月卖出的双数×(1+10%)=现在卖出的双数,依此列出方程即可.
【解答】解:设上个月卖出x双,根据题意得
(1+10%)x=330.
故选D.
8.如图,已知线段AB,分别以A、B为圆心,大于![]() AB为半径作弧,连接弧的交点得到直线l,在直线l上取一点C,使得∠CAB=25°,延长AC至M,求∠BCM的度数为()
AB为半径作弧,连接弧的交点得到直线l,在直线l上取一点C,使得∠CAB=25°,延长AC至M,求∠BCM的度数为()
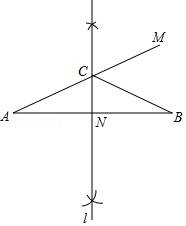
A.40° B.50° C.60° D.70°
【考点】N2:作图—基本作图;KG:线段垂直平分线的性质.
【分析】根据作法可知直线l是线段AB的垂直平分线,故可得出AC=BC,再由三角形外角的性质即可得出结论.
【解答】解:∵由作法可知直线l是线段AB的垂直平分线,
∴AC=BC,
∴∠CAB=∠CBA=25°,
∴∠BCM=∠CAB+∠CBA=25°+25°=50°.
故选B.
9.下列哪一个是假命题()
A.五边形外角和为360°
B.切线垂直于经过切点的半径
C.(3,﹣2)关于y轴的对称点为(﹣3,2)
D.抛物线y=x2﹣4x+2017对称轴为直线x=2
【考点】O1:命题与定理.
【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
【解答】解:A、五边形外角和为360°是真命题,故A不符合题意;
B、切线垂直于经过切点的半径是真命题,故B不符合题意;
C、(3,﹣2)关于y轴的对称点为(﹣3,2)是假命题,故C符合题意;
D、抛物线y=x2﹣4x+2017对称轴为直线x=2是真命题,故D不符合题意;
故选:C.
10.某共享单车前a公里1元,超过a公里的,每公里2元,若要使使用该共享单车50%的人只花1元钱,a应该要取什么数()
A.平均数 B.中位数 C.众数 D.方差
【考点】WA:统计量的选择.
【分析】由于要使使用该共享单车50%的人只花1元钱,根据中位数的意义分析即可
【解答】解:根据中位数的意义,
故只要知道中位数就可以了.
故选B.
11.如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10cm,则树AB的高度是()m.

A.20![]() B.30 C.30
B.30 C.30![]() D.40
D.40
【考点】TA:解直角三角形的应用﹣仰角俯角问题.
【分析】先根据CD=20米,DE=10m得出∠DCE=30°,故可得出∠DCB=90°,再由∠BDF=30°可知∠DBE=60°,由DF∥AE可得出∠BGF=∠BCA=60°,故∠GBF=30°,所以∠DBC=30°,再由锐角三角函数的定义即可得出结论.
【解答】解:在Rt△CDE中,
∵CD=20m,DE=10m,
∴sin∠DCE=![]() =
=![]() ,
,
∴∠DCE=30°.
∵∠ACB=60°,DF∥AE,
∴∠BGF=60°
∴∠ABC=30°,∠DCB=90°.
∵∠BDF=30°,
∴∠DBF=60°,
∴∠DBC=30°,
∴BC=![]() =
=![]() =20
=20![]() m,
m,
∴AB=BC•sin60°=20![]() ×
×![]() =30m.
=30m.
故选B.
12.如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OE•OP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=![]() ,其中正确结论的个数是()
,其中正确结论的个数是()
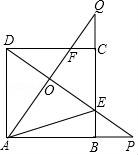
A.1 B.2 C.3 D.4
【考点】S9:相似三角形的判定与性质;KD:全等三角形的判定与性质;LE:正方形的性质;T7:解直角三角形.
【分析】由四边形ABCD是正方形,得到AD=BC,∠DAB=∠ABC=90°,根据全等三角形的性质得到∠P=∠Q,根据余角的性质得到AQ⊥DP;故①正确;根据相似三角形的性质得到AO2=OD•OP,由OD≠OE,得到OA2≠OE•OP;故②错误;根据全等三角形的性质得到CF=BE,DF=CE,于是得到S△ADF﹣S△DFO=S△DCE﹣S△DOF,即S△AOD=S四边形OECF;故③正确;根据相似三角形的性质得到BE=![]() ,求得QE=
,求得QE=![]() ,QO=
,QO=![]() ,OE=
,OE=![]() ,由三角函数的定义即可得到结论.
,由三角函数的定义即可得到结论.
【解答】解:∵四边形ABCD是正方形,
∴AD=BC,∠DAB=∠ABC=90°,
∵BP=CQ,
∴AP=BQ,
在△DAP与△ABQ中, ,
,
∴△DAP≌△ABQ,
∴∠P=∠Q,
∵∠Q+∠QAB=90°,
∴∠P+∠QAB=90°,
∴∠AOP=90°,
∴AQ⊥DP;
故①正确;
∵∠DOA=∠AOP=90,∠ADO+∠P=∠ADO+∠DAO=90°,
∴∠DAO=∠P,
∴△DAO∽△APO,
∴![]() ,
,
∴AO2=OD•OP,
∵AE>AB,
∴AE>AD,
∴OD≠OE,
∴OA2≠OE•OP;故②错误;
在△CQF与△BPE中 ,
,
∴△CQF≌△BPE,
∴CF=BE,
∴DF=CE,
在△ADF与△DCE中,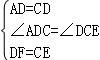 ,
,
∴△ADF≌△DCE,
∴S△ADF﹣S△DFO=S△DCE﹣S△DOF,
即S△AOD=S四边形OECF;故③正确;
∵BP=1,AB=3,
∴AP=4,
∵△AOP∽△DAP,
∴![]() ,
,
∴BE=![]() ,∴QE=
,∴QE=![]() ,
,
∵△QOE∽△PAD,
∴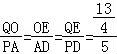 ,
,
∴QO=![]() ,OE=
,OE=![]() ,
,
∴AO=5﹣QO=![]() ,
,
∴tan∠OAE=![]() =
=![]() ,故④正确,
,故④正确,
故选C.
二、填空题
13.因式分解:a3﹣4a= a(a+2)(a﹣2) .
【考点】55:提公因式法与公式法的综合运用.
【分析】首先提取公因式a,进而利用平方差公式分解因式得出即可.
【解答】解:a3﹣4a=a(a2﹣4)=a(a+2)(a﹣2).
故答案为:a(a+2)(a﹣2).
14.在一个不透明的袋子里,有2个黑球和1个白球,除了颜色外全部相同,任意摸两个球,摸到1黑1白的概率是 ![]() .
.
【考点】X6:列表法与树状图法.
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所摸到1黑1白的情况,再利用概率公式即可求得答案.
【解答】解:依题意画树状图得:

∵共有6种等可能的结果,所摸到的球恰好为1黑1白的有4种情况,
∴所摸到的球恰好为1黑1白的概率是:![]() =
=![]() .
.
故答案为:![]() .
.
15.阅读理解:引入新数i,新数i满足分配律,结合律,交换律,已知i2=﹣1,那么(1+i)•(1﹣i)= 2 .
【考点】4F:平方差公式;2C:实数的运算.
【分析】根据定义即可求出答案.
【解答】解:由题意可知:原式=1﹣i2=1﹣(﹣1)=2
故答案为:2
16.如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,Rt△MPN,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP= 3 .

【考点】S9:相似三角形的判定与性质.
【分析】如图作PQ⊥AB于Q,PR⊥BC于R.由△QPE∽△RPF,推出![]() =
=![]() =2,可得PQ=2PR=2BQ,由PQ∥BC,可得AQ:QP:AP=AB:BC:AC=3:4:5,设PQ=4x,则AQ=3x,AP=5x,BQ=2x,可得2x+3x=3,求出x即可解决问题.
=2,可得PQ=2PR=2BQ,由PQ∥BC,可得AQ:QP:AP=AB:BC:AC=3:4:5,设PQ=4x,则AQ=3x,AP=5x,BQ=2x,可得2x+3x=3,求出x即可解决问题.
【解答】解:如图作PQ⊥AB于Q,PR⊥BC于R.
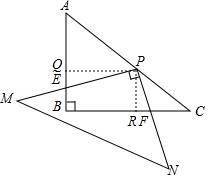
∵∠PQB=∠QBR=∠BRP=90°,
∴四边形PQBR是矩形,
∴∠QPR=90°=∠MPN,
∴∠QPE=∠RPF,
∴△QPE∽△RPF,
∴![]() =
=![]() =2,
=2,
∴PQ=2PR=2BQ,
∵PQ∥BC,
∴AQ:QP:AP=AB:BC:AC=3:4:5,设PQ=4x,则AQ=3x,AP=5x,BQ=2x,
∴2x+3x=3,
∴x=![]() ,
,
∴AP=5x=3.
故答案为3.
三、解答题
17.计算:|![]() ﹣2|﹣2cos45°+(﹣1)﹣2+
﹣2|﹣2cos45°+(﹣1)﹣2+![]() .
.
【考点】2C:实数的运算;6F:负整数指数幂;T5:特殊角的三角函数值.
【分析】因为![]() <2,所以|
<2,所以|![]() ﹣2|=2﹣
﹣2|=2﹣![]() ,cos45°=
,cos45°=![]() ,
,![]() =2
=2![]() ,分别计算后相加即可.
,分别计算后相加即可.
【解答】解:|![]() ﹣2|﹣2cos45°+(﹣1)﹣2+
﹣2|﹣2cos45°+(﹣1)﹣2+![]() ,
,
=2﹣![]() ﹣2×
﹣2×![]() +1+2
+1+2![]() ,
,
=2﹣![]() ﹣
﹣![]() +1+2
+1+2![]() ,
,
=3.
18.先化简,再求值:(![]() +
+![]() )÷
)÷![]() ,其中x=﹣1.
,其中x=﹣1.
【考点】6D:分式的化简求值.
【分析】根据分式的运算法则即可求出答案.
【解答】解:当x=﹣1时,
原式=![]() ×
×![]()
=3x+2
=﹣1
19.深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.
类型 | 频数 | 频率 |
A | 30 | x |
B | 18 | 0.15 |
C | m | 0.40 |
D | n | y |
(1)学生共 120 人,x= 0.25 ,y= 0.2 ;
(2)补全条形统计图;
(3)若该校共有2000人,骑共享单车的有 500 人.

【考点】VC:条形统计图;V5:用样本估计总体;V7:频数(率)分布表.
【分析】(1)根据B类学生坐公交车、私家车的人数以及频率,求出总人数,再根据频数与频率的关系一一解决即可;
(2)求出m、n的值,画出条形图即可;
(3)用样本估计总体的思想即可解决问题;
【解答】解:(1)由题意总人数=![]() =120人,
=120人,
x=![]() =0.25,m=120×0.4=48,
=0.25,m=120×0.4=48,
y=1﹣0.25﹣0.4﹣0.15=0.2,
n=120×0.2=24,
(2)条形图如图所示,

(3)2000×0.25=500人,
故答案为500.
20.一个矩形周长为56厘米.
(1)当矩形面积为180平方厘米时,长宽分别为多少?
(2)能围成面积为200平方米的矩形吗?请说明理由.
【考点】AD:一元二次方程的应用.
【分析】(1)设出矩形的一边长为未知数,用周长公式表示出另一边长,根据面积列出相应方程求解即可.
(2)同样列出方程,若方程有解则可,否则就不可以.
【解答】解:(1)设矩形的长为x厘米,则另一边长为(28﹣x)厘米,依题意有
x(28﹣x)=180,
解得x1=10(舍去),x2=18,
28﹣x=28﹣18=10.
故长为18厘米,宽为10厘米;
(2)设矩形的长为x厘米,则宽为(28﹣x)厘米,依题意有
x(28﹣x)=200,
即x2﹣28x+200=0,
则△=282﹣4×200=784﹣800<0,原方程无解,
故不能围成一个面积为200平方厘米的矩形.
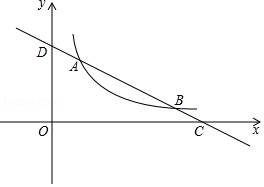
21.如图,一次函数y=kx+b与反比例函数y=![]() (x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(1)直接写出一次函数y=kx+b的表达式和反比例函数y=![]() (x>0)的表达式;
(x>0)的表达式;
(2)求证:AD=BC.
【考点】G8:反比例函数与一次函数的交点问题.
【分析】(1)先确定出反比例函数的解析式,进而求出点B的坐标,最后用待定系数法求出直线AB的解析式;
(2)由(1)知,直线AB的解析式,进而求出C,D坐标,构造直角三角形,利用勾股定理即可得出结论.
【解答】解:(1)将点A(2,4)代入y=![]() 中,得,m=2×4=8,
中,得,m=2×4=8,
∴反比例函数的解析式为y=![]() ,
,
将点B(a,1)代入y=![]() 中,得,a=8,
中,得,a=8,
∴B(8,1),
将点A(2,4),B(8,1)代入y=kx+b中,得,![]() ,
,
∴![]() ,
,
∴一次函数解析式为y=﹣![]() x+5;
x+5;
(2)∵直线AB的解析式为y=﹣![]() x+5,
x+5,
∴C(10,0),D(0,5),
如图,
过点A作AE⊥y轴于E,过点B作BF⊥x轴于F,
∴E(0,4),F(8,0),
∴AE=2,DE=1,BF=1,CF=2,
在Rt△ADE中,根据勾股定理得,AD=![]() =
=![]() ,
,
在Rt△BCF中,根据勾股定理得,BC=![]() =
=![]() ,
,
∴AD=BC.
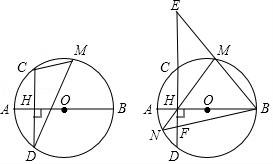
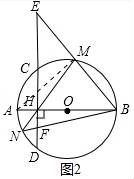
22.如图,线段AB是⊙O的直径,弦CD⊥AB于点H,点M是![]() 上任意一点,AH=2,CH=4.
上任意一点,AH=2,CH=4.
(1)求⊙O的半径r的长度;
(2)求sin∠CMD;
(3)直线BM交直线CD于点E,直线MH交⊙O于点N,连接BN交CE于点F,求HE•HF的值.
【考点】MR:圆的综合题.
【分析】(1)在Rt△COH中,利用勾股定理即可解决问题;
(2)只要证明∠CMD=△COA,求出sin∠COA即可;
(3)由△EHM∽△NHF,推出![]() =
=![]() ,推出HE•HF=HM•HN,又HM•HN=AH•HB,推出HE•HF=AH•HB,由此即可解决问题.
,推出HE•HF=HM•HN,又HM•HN=AH•HB,推出HE•HF=AH•HB,由此即可解决问题.
【解答】解:(1)如图1中,连接OC.
∵AB⊥CD,
∴∠CHO=90°,
在Rt△COH中,∵OC=r,OH=r﹣2,CH=4,
∴r2=42+(r﹣2)2,
∴r=5.
(2)如图1中,连接OD.
∵AB⊥CD,AB是直径,
∴![]() =
=![]() =
=![]()
![]() ,
,
∴∠AOC=![]() ∠COD,
∠COD,
∵∠CMD=![]() ∠COD,
∠COD,
∴∠CMD=∠COA,
∴sin∠CMD=sin∠COA=![]() =
=![]() .
.
(3)如图2中,连接AM.
∵AB是直径,
∴∠AMB=90°,
∴∠MAB+∠ABM=90°,
∵∠E+∠ABM=90°,
∴∠E=∠MAB,
∴∠MAB=∠MNB=∠E,
∵∠EHM=∠NHFM
∴△EHM∽△NHF,
∴![]() =
=![]() ,
,
∴HE•HF=HM•HN,
∵HM•HN=AH•HB,
∴HE•HF=AH•HB=2•(10﹣2)=16.

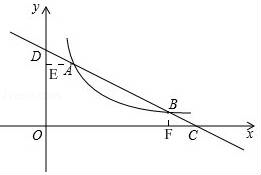
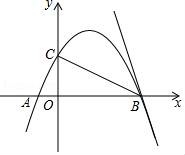
23.如图,抛物线y=ax2+bx+2经过点A(﹣1,0),B(4,0),交y轴于点C;
(1)求抛物线的解析式(用一般式表示);
(2)点D为y轴右侧抛物线上一点,是否存在点D使S△ABC=![]() S△ABD?若存在请直接给出点D坐标;若不存在请说明理由;
S△ABD?若存在请直接给出点D坐标;若不存在请说明理由;
(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长.
【考点】HF:二次函数综合题.
【分析】(1)由A、B的坐标,利用待定系数法可求得抛物线解析式;
(2)由条件可求得点D到x轴的距离,即可求得D点的纵坐标,代入抛物线解析式可求得D点坐标;
(3)由条件可证得BC⊥AC,设直线AC和BE交于点F,过F作FM⊥x轴于点M,则可得BF=BC,利用平行线分线段成比例可求得F点的坐标,利用待定系数法可求得直线BE解析式,联立直线BE和抛物线解析式可求得E点坐标,则可求得BE的长.
【解答】解:
(1)∵抛物线y=ax2+bx+2经过点A(﹣1,0),B(4,0),
∴![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)由题意可知C(0,2),A(﹣1,0),B(4,0),
∴AB=5,OC=2,
∴S△ABC=![]() AB•OC=
AB•OC=![]() ×5×2=5,
×5×2=5,
∵S△ABC=![]() S△ABD,
S△ABD,
∴S△ABD=![]() ×5=
×5=![]() ,
,
设D(x,y),
∴![]() AB•|y|=
AB•|y|=![]() ×5|y|=
×5|y|=![]() ,解得|y|=3,
,解得|y|=3,
当y=3时,由﹣![]() x2+
x2+![]() x+2=3,解得x=1或x=2,此时D点坐标为(1,3)或(2,3);
x+2=3,解得x=1或x=2,此时D点坐标为(1,3)或(2,3);
当y=﹣3时,由﹣![]() x2+
x2+![]() x+2=﹣3,解得x=﹣2(舍去)或x=5,此时D点坐标为(5,﹣3);
x+2=﹣3,解得x=﹣2(舍去)或x=5,此时D点坐标为(5,﹣3);
综上可知存在满足条件的点D,其坐标为(1,3)或(2,3)或(5,﹣3);
(3)∵AO=1,OC=2,OB=4,AB=5,
∴AC=![]() =
=![]() ,BC=
,BC=![]() =2
=2![]() ,
,
∴AC2+BC2=AB2,
∴△ABC为直角三角形,即BC⊥AC,
如图,设直线AC与直线BE交于点F,过F作FM⊥x轴于点M,

由题意可知∠FBC=45°,
∴∠CFB=45°,
∴CF=BC=2![]() ,
,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得OM=2,
,解得OM=2,![]() =
=![]() ,即
,即![]() =
=![]() ,解得FM=6,
,解得FM=6,
∴F(2,6),且B(4,0),
设直线BE解析式为y=kx+m,则可得![]() ,解得
,解得![]() ,
,
∴直线BE解析式为y=﹣3x+12,
联立直线BE和抛物线解析式可得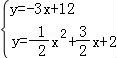 ,解得
,解得![]() 或
或![]() ,
,
∴E(5,﹣3),
∴BE=![]() =.
=.
第1页(共26页)