请选择
2017-2018东莞市九年级数学试题【word版含答案】
由于版式的问题,试题可能会出现乱码的现象,为了方便您的阅读请点击全屏查看
一.单选题(共12题;共36分)
1.方程2(2x+1)(x﹣3)=0的两根分别为( )
A. ![]() 和3 B. ﹣
和3 B. ﹣ ![]() 和3 C.
和3 C. ![]() 和﹣3 D. ﹣
和﹣3 D. ﹣ ![]() 和﹣3
和﹣3
2.下列性质中菱形不一定具有的性质是( )
A. 对角线互相平分 B. 对角线互相垂直 C. 对角线相等 D. 既是轴对称图形又是中心对称图形
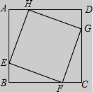 3.如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
3.如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
A. 30 B. 34 C. 36D. 40
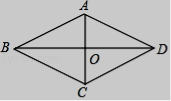
4.求证:菱形的两条对角线互相垂直. 已知:如图,四边形ABCD是菱形,对角线AC,BD交于点O.
求证:AC⊥BD.
以下是排乱的证明过程:
①又BO=DO;②∴AO⊥BD,即AC⊥BD;③∵四边形ABCD是菱形;④∴AB=AD.
证明步骤正确的顺序是( )
A. ③→②→①→④ B. ③→④→①→② C. ①→②→④→③ D. ①→④→③→②
5.下列关于矩形的说法,正确的是( )
A. 对角线相等的四边形是矩形 B. 对角线互相平分的四边形是矩形
C. 矩形的对角线相等且互相平分 D. 矩形的对角线互相垂直且平分
6.若x1 , x2是方程x2﹣2mx+m2﹣m﹣1=0的两个根,且x1+x2=1﹣x1x2 , 则m的值为( )
A. ﹣1或2 B. 1或﹣2 C. ﹣2 D. 1
7.一个不透明的布袋里装有5个红球、2个白球、3个黄球,它们除颜色外其余都相同.从袋中任意找出1个球,是黄球的概率为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8.下列命题中:
①两条对角线互相平分且相等的四边形是正方形;②菱形的一条对角线平分一组对角;
③顺次连结四边形各边中点所得的四边形是平行四边形;
④两条对角线互相平分的四边形是矩形;⑤平行四边形对角线相等.
真命题的个数是( )
A. 1 B. 2 C. 3 D. 4
9.随机掷一枚均匀的硬币20次,其中有8次出现正面,12次出现反面,则掷这枚均匀硬币出现正面的概率是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10.若关于x的一元二次方程mx2﹣2x﹣1=0无实数根,则一次函数y=(m+1)x﹣m的图象不经过()
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
11.正方形具备而菱形不具备的性质是()
A. 对角线互相平分 B. 对角线互相垂直 C. 对角线相等 D. 每条对角线平分一组对角
12.在国务院房地产调控政策影响下,建德市区房价逐步下降,2012年10月份的房价平均每平方米为11000元,预计2014年10月的房价平均每平方米回落到7800元,假设这两年我市房价的平均下跌率均为![]() , 则关于
, 则关于![]() 的方程为( )
的方程为( )
A. 11000(1+x)2=7800 B. 11000(1-x)2=7800 C. 11000(1-x)2=3200 D. 3200(1-x)2=7800
二.填空题(共9题;共18分)
13.若一个三角形的三边长均满足方程x2﹣6x+8=0,则此三角形的周为________.
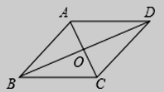
14.如图,四边形ABCD的对角线互相平分,若再补充一个条件能使四边形ABCD成为矩形,则这个条件是________ (只填一个条件即可)
15.如果关于x的方程x2+2(a+1)x+2a+1=0有一个小于1的正数根,那么实数a的取值范围是________
16.正方形ABCD的边长为8,点E为正方形边上一点,连接BE,且BE=10,则AE的长为________.
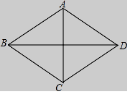
17.如图,在菱形ABCD中,若AC=6,BD=8,则菱形ABCD的面积是________.
18.矩形ABCD中,AB=5,BC=12,对角线AC,BD交于点O,E,F分别为AB,AO中点,则线段EF=________
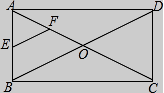
19.如图,某小区有一块长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们面积之和为60米2 , 两块绿地之间及周边留有宽度相等的人行通道,则人行道的宽度为________米.

20.已知一元二次方程2x2﹣3x﹣1=0的两根为x1 , x2 , 则x1•x2=________.
21.抽屉里放着黑白两种颜色的袜子各1双(除颜色外其余都相同),在看不见的情况下随机摸出两只袜子,它们恰好同色的概率是________
三.解方程(共3题;共13分)
22. (y﹣1)2+3(y﹣1)=0.
23. x2+3x﹣2=0.
24.(1) 3(x﹣2)2=x(x﹣2)
四.解答题(共1题;共10分)
25.李老师为了解学生完成数学课前预习的具体情况,对部分学生进行了跟踪调查,并将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)李老师一共调查了多少名同学?
(2)C类女生有________名,D类男生有________名,将下面条形统计图补充完整;
(3)为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行
“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
四.综合题(共3题;共23分)
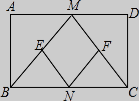
26.已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
27.在一只不透明的袋中,装着标有数字3,4,5,7的质地、大小均相同的小球,小明和小东同时从袋中随机各摸出1个球,并计算这两个球上的数字之和,当和小于9时小明获胜,反之小东获胜.
(1)请用树状图或列表的方法,求小明获胜的概率;
(2)这个游戏公平吗?请说明理由.
28.为进一步发展基础教育,自2014年以来,某县加大了教育经费的投入,2014年该县投入教育经费6000万元.2016年投入教育经费8640万元.假设该县这两年投入教育经费的年平均增长率相同.
(1)求这两年该县投入教育经费的年平均增长率;
(2)若该县教育经费的投入还将保持相同的年平均增长率,请你预算2017年该县投入教育经费多少万元.
2017-2018东莞市九年级数学试题参考答案
一.单选题
1.【答案】B
【考点】解一元二次方程-因式分解法
【解析】【解答】解:2(2x+1)(x﹣3)=0,
2x+1=0,x﹣3=0,
x1=﹣ ![]() ,x2=3,
,x2=3,
故选B.
【分析】根据已知方程得出两个一元一次方程,求出方程的解即可.
2.【答案】C
【考点】菱形的性质
【解析】【解答】解:A、菱形的对角线互相平分,此选项正确; B、菱形的对角线互相垂直,此选项正确;
C、菱形的对角线不一定相等,此选项错误;
D、菱形既是轴对称图形又是中心对称图形,此选项正确;
故选:C.
【分析】根据菱形的性质解答即可得.
3.【答案】B
【考点】全等三角形的判定与性质,正方形的判定与性质
【解析】【解答】解:∵四边形ABCD是正方形, ∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵AE=BF=CG=DH,
∴AH=BE=CF=DG.
在△AEH、△BFE、△CGF和△DHG中,
 ,
,
∴△AEH≌△BFE≌△CGF≌△DHG(SAS),
∴EH=FE=GF=GH,∠AEH=∠BFE,
∴四边形EFGH是菱形,
∵∠BEF+∠BFE=90°,
∴∠BEF+∠AEH=90°,
∴∠HEF=90°,
∴四边形EFGH是正方形,
∵AB=BC=CD=DA=8,AE=BF=CG=DH=5,
∴EH=FE=GF=GH= ![]() =
= ![]() ,
,
∴四边形EFGH的面积是: ![]() ×
× ![]() =34,
=34,
故选B.
【分析】由正方形的性质得出∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,证出AH=BE=CF=DG,由SAS证明△AEH≌△BFE≌△CGF≌△DHG,得出EH=FE=GF=GH,∠AEH=∠BFE,证出四边形EFGH是菱形,再证出∠HEF=90°,即可得出四边形EFGH是正方形,由边长为8,AE=BF=CG=DH=5,可得AH=3,由勾股定理得EH,得正方形EFGH的面积.
4.【答案】B
【考点】菱形的性质
【解析】【解答】证明: ∵四边形ABCD是菱形,
∴AB=AD,
∵对角线AC,BD交于点O,
∴BO=DO,
∴AO⊥BD,
即AC⊥BD,
∴证明步骤正确的顺序是③→④→①→②,
故选B.
【分析】根据菱形是特殊的平行四边形以及等腰三角形的性质证明即可.
5.【答案】C
【考点】矩形的判定与性质
【解析】【解答】解:A、对角线相等的四边形是矩形,不正确; B、对角线互相平分的四边形是矩形,不正确;
C、矩形的对角线相等且互相平分,正确;
D、矩形的对角线互相垂直且平分,不正确;
故选:C.
【分析】由矩形的判定与性质分别作出判断,即可得出结论.
6.【答案】D
【考点】根与系数的关系
【解析】【解答】解:∵x1 , x2是方程x2﹣2mx+m2﹣m﹣1=0的两个根, ∴x1+x2=2m,x1•x2=m2﹣m﹣1.
∵x1+x2=1﹣x1x2 ,
∴2m=1﹣(m2﹣m﹣1),即m2+m﹣2=(m+2)(m﹣1)=0,
解得:m1=﹣2,m2=1.
∵方程x2﹣2mx+m2﹣m﹣1=0有实数根,
∴△=(﹣2m)2﹣4(m2﹣m﹣1)=4m+4≥0,
解得:m≥﹣1.
∴m=1.
故选D.
【分析】根据根与系数的关系结合x1+x2=1﹣x1x2 , 即可得出关于m的一元二次方程,解之即可得出m的值,再根据方程有实数根结合根的判别式,即可得出关于m的一元一次不等式,解之即可得出m的取值范围,从而可确定m的值.
7.【答案】C
【考点】列表法与树状图法
【解析】【解答】解: ∵从装有5个红球、2个白球、3个黄球的袋中任意摸出1个球有10种等可能结果,其中摸出的球是黄球的结果有3种,
∴从袋中任意摸出1个球是黄球的概率为:![]() .
.
故答案为C.
【分析】依题可得共有10种等可能结果,其中摸出的球是黄球的结果有3中,利用概率公式即可得出答案.
8.【答案】B
【考点】正方形的判定与性质
【解析】【解答】解:①两条对角线互相平分且相等的四边形是矩形,故错误;
②菱形的一条对角线平分一组对角,正确,为真命题;
③顺次连结四边形各边中点所得的四边形是平行四边形,正确,为真命题;
④两条对角线互相平分的四边形是平行四边形,错误,为假命题;
⑤平行四边形对角线相等,错误,为假命题,
正确的有2个,
故选B.
【分析】利用正方形的判定定理、菱形的判定定理、矩形的判定定理、平行四边形的判定及性质分别判断后即可确定正确的选项.
9.【答案】B
【考点】利用频率估计概率
【解析】【解答】解:抛一枚均匀硬币出现正面和反面的概率是相等的,都是![]() .
.
故选B.
【分析】抛一枚均匀硬币出现正面和反面的概率是相等的,都是![]() .
.
10.【答案】C
【考点】根的判别式
【解析】【解答】解:根据题意得m≠0且△=(﹣2)2﹣4m×(﹣1)<0,
解得m<﹣1,
所以一次函数y=(m+1)x﹣m的图象第一、二、四象限.
故选C.
【分析】根据判别式的意义得到m≠0且△=(﹣2)2﹣4m×(﹣1)<0,解得m<﹣1,然后根据一次函数的性质求解.
11.【答案】C
【考点】菱形的性质,正方形的性质
【解析】【分析】正方形具有矩形和菱形的性质,故根据正方形和菱形的性质即可解题。
A、平行四边形的对角线互相平分,所以菱形和正方形对角线均互相平分,故本选项错误;
B、菱形和正方形的对角线均互相垂直,故本选项错误;
C、正方形对角线相等,而菱形对角线不相等,故本选项正确;
D、对角线即角平分线是菱形的性质,正方形具有全部菱形的性质,所以本选项错误。
故选 C.
12.【答案】B
【考点】一元二次方程的应用
【解析】【分析】依题意知这两年我市房价的平均下跌率均为x,故第一次降价为11000(1-x)元,
第二次降价为11000(1-x)2=7800
故选B.
【点评】本题难度较低,主要考查学生对一元二次方程解决销售问题实际应用能力。为中考常见题型,要求学生牢固掌握。
二.填空题
13.【答案】6或10或12
【考点】解一元二次方程-因式分解法,三角形三边关系
【解析】【解答】∵x2﹣6x+8=0,
∴(x-2)(x-4)=0,
∴x1=2,x2=4,
①当4为腰,2为底时,
∴C三角形=4+4+2=10,
②当2为腰,4为底时,
∵2+2=4,
∴ 不能构成三角形,
③当三角形三边都是4时,
∴C三角形=4+4+4=12,
④当三角形三边都是2时,
∴C三角形=2+2+2=6,
故答案为:6,10或12.
【分析】先解一元二次方程求出根为2或4,之后分情况讨论三角形三边的长度,从而求出其周长.
14.【答案】AC=BD(答案不唯一)
【考点】矩形的判定
【解析】【解答】解:可添加AC=BD,理由如下:
∵四边形ABCD的对角线互相平分,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴四边形ABCD是矩形.
故答案为:AC=BD(答案不唯一).
【分析】由四边形ABCD的对角线互相平分,可得四边形ABCD是平行四边形,再添加AC=BD,可根据对角线相等的平行四边形是矩形即可得出结论.
15.【答案】![]()
【考点】解一元二次方程-公式法
【解析】【解答】解:根据方程的求根公式可得:
x=[(﹣2(a+1)±![]() ]÷2=[(﹣2a﹣2)±2a]÷2=﹣a﹣1±a,
]÷2=[(﹣2a﹣2)±2a]÷2=﹣a﹣1±a,
则方程的两根为﹣1或﹣2a﹣1,
或(x+1)(x+2a+1)=0,
解得x1=﹣1,x2=﹣2a﹣1,
∵﹣1<0,
∴小于1的正数根只能为﹣2a﹣1,
即0<﹣2a﹣1<1,
解得﹣1<a<﹣![]() .
.
故填空答案为﹣1<a<﹣![]() .
.
【分析】先利用方程的求根公式表示出方程的两个根,再利用“有一个小于1的正数根”这一条件确定a的取值范围.
16.【答案】6或2 ![]()
【考点】正方形的性质
【解析】【解答】解: 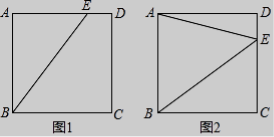
①如图1,点E在AD上时,
根据勾股定理得,AE= ![]() =
= ![]() =6;
=6;
②如图2,点E在CD上时,
根据勾股定理得,CE= ![]() =
= ![]() =6,
=6,
所以,DE=CD﹣CE=8﹣6=2,
在Rt△ADE中,根据勾股定理得,AE= ![]() =
= ![]() =2
=2 ![]() ,
,
综上所述,AE的长为6或2 ![]() .
.
故答案为:6或2 ![]() .
.
【分析】作出图形,然后分①点E在AD上时,利用勾股定理列式求解即可得到AE,②点E在CD上时,利用勾股定理列式求出CE,再求出DE,然后利用勾股定理列式计算即可得解.
17.【答案】24
【考点】菱形的性质
【解析】【解答】解: ∵菱形ABCD的对角线AC=6,BD=8,
∴菱形的面积S= ![]() AC•BD=
AC•BD= ![]() ×8×6=24.
×8×6=24.
故答案为:24.
【分析】根据菱形的面积等于对角线乘积的一半列式计算即可得解.
18.【答案】134
【考点】三角形中位线定理,矩形的性质
【解析】【解答】解:∵四边形ABCD是矩形, ∴∠ABC=90°,OB= 12 BD,AD=BC=12,
∴BD= AB2+AD2 = 122+52 =13,
∴OB= 132 ,
∵点E、F分别是AB、AO的中点,
∴EF是△AOB的中位线,
∴EF= 12 OB= 134 ;
故答案为: 134 .
【分析】先由勾股定理求出BD,再得出OB,证明EF是△AOB的中位线,即可得出结果.
19.【答案】1
【考点】一元二次方程的应用
【解析】【解答】解:设人行道的宽度为x米(0<x<3),根据题意得:
(18﹣3x)(6﹣2x)=60,
整理得,(x﹣1)(x﹣8)=0.
解得:x1=1,x2=8(不合题意,舍去).
即:人行通道的宽度是1米.
故答案是:1.
【分析】设人行道的宽度为x米,根据矩形绿地的面积之和为60米2 , 列出一元二次方程,再进行求解即可得出答案.
20.【答案】![]()
【考点】根与系数的关系
【解析】【解答】解:∵一元二次方程2x2﹣3x﹣1=0的两根为x1 , x2 , ∴x1•x2= ![]() =﹣
=﹣ ![]() .
.
故填空答案为﹣ ![]() .
.
【分析】直接根据一元二次方程的根与系数的关系可以得到x1•x2 .
21.【答案】13
【考点】列表法与树状图法
【解析】【解答】解:画树状图得:
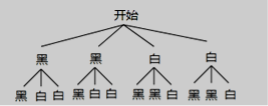
∵共有12种等可能的结果,它们恰好同色的有4种情况,
∴它们恰好同色的概率是:412=13 .
故答案为:13 .
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与它们恰好同色的情况,再利用概率公式即可求得答案.
三.解答题
25.【答案】(1)解:(1+2)÷15%=20(人).
(2)3;1
(3)解:如下树状图可得![]() .
.

【考点】扇形统计图,条形统计图,列表法与树状图法,概率公式
【解析】【解答】(2)C类学生人数:20×25%=5(名)
C类女生人数:5-2=3(名),
D类学生占的百分比:1-15%-50%-25%=10%,
D类学生人数:20×10%=2(名),
D类男生人数:2-1=1(名),补充图如下:
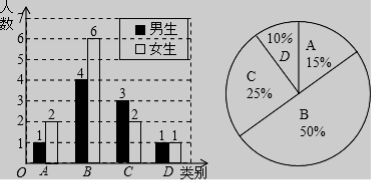
故答案为3;1.
【分析】(1)组别的人数÷百分比=总人数;
(2)C级的女生人数=C的总人数-C的男生人数;
D级的男生人数=D的总人数-D的女生人数;
(3)用树状图列举出所有情况,再找出(一位男同学,一位女同学)的情况数量,用概率公式计算即可.
四.综合题
23.【答案】(1)解:根据题意画图如下: 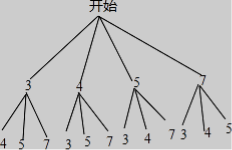
∵从表中可以看出所有可能结果共有12种,其中数字之和小于9的有4种,
∴P(小明获胜)= ![]() =
= ![]() ;
;
(2)解:∵P(小明获胜)= ![]() , ∴P(小东获胜)=1﹣
, ∴P(小东获胜)=1﹣ ![]() =
= ![]() ,
,
∴这个游戏不公平.
【考点】列表法与树状图法,游戏公平性
【解析】【分析】(1)先根据题意画出树状图,再根据概率公式即可得出答案;(2)先分别求出小明和小东的概率,再进行比较即可得出答案.
24.【答案】(1)解:设该县投入教育经费的年平均增长率为x,根据题意得: 6000(1+x)2=8640
解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去),
答:该县投入教育经费的年平均增长率为20%
(2)解:因为2016年该县投入教育经费为8640万元,且增长率为20%, 所以2017年该县投入教育经费为:y=8640×(1+0.2)=10368(万元),
答:预算2017年该县投入教育经费10368万元
【考点】一元二次方程的应用
【解析】【分析】(1)设该县投入教育经费的年平均增长率为x,根据2014年该县投入教育经费6000万元和2016年投入教育经费8640万元列出方程,再求解即可;(2)根据2016年该县投入教育经费和每年的增长率,直接得出2017年该县投入教育经费为8640×(1+0.2),再进行计算即可.
25.【答案】(1)证明:∵四边形ABCD是矩形, ∴∠A=∠D=90°,AB=DC,
∵M是AD的中点,
∴AM=DM,
在△ABM和△DCM中, 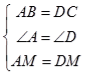 ,
,
∴△ABM≌△DCM(SAS)
(2)解:四边形MENF是菱形;理由如下: 由(1)得:△ABM≌△DCM,
∴BM=CM,
∵E、F分别是线段BM、CM的中点,
∴ME=BE= ![]() BM,MF=CF=
BM,MF=CF= ![]() CM,
CM,
∴ME=MF,
又∵N是BC的中点,
∴EN、FN是△BCM的中位线,
∴EN= ![]() CM,FN=
CM,FN= ![]() BM,
BM,
∴EN=FN=ME=MF,
∴四边形MENF是菱形.
【考点】全等三角形的判定与性质,矩形的性质
【解析】【分析】(1)由矩形的性质得出AB=DC,∠A=∠D,再由M是AD的中点,根据SAS即可证明△ABM≌△DCM;(2)先由(1)得出BM=CM,再由已知条件证出ME=MF,EN、FN是△BCM的中位线,即可证出EN=FN=ME=MF,得出四边形MENF是菱形.
五.计算题
22.【答案】解:因式分解得,(y﹣1)(y﹣1+3)=0,
∴y﹣1=0或y+2=0,
∴y1=1,y2=﹣2.
【考点】解一元二次方程-因式分解法
【解析】【分析】把y﹣1看作整体,用因式分解法解一元二次方程即可.
23.【答案】解:∵a=1,b=3,c=﹣2,
∴△=b2﹣4ac=32﹣4×1×(﹣2)=17,
∴x= ![]() ,
,
∴x1= ![]() ,x2=
,x2= ![]() .
.
【考点】解一元二次方程-因式分解法
【解析】【分析】求出b2﹣4ac的值,代入公式求出即可.
24.【答案】(1)解:左边因式分解可得:(x﹣1)(3x+7)=0, ∴x﹣1=0或3x+7=0,
解得:x=1或x=﹣ ![]() ;
;
(2)解:∵3(x﹣2)2﹣x(x﹣2)=0, ∴(x﹣2)[3(x﹣2)﹣x]=0,即(x﹣2)(2x﹣6)=0,
∴x﹣2=0或2x﹣6=0,
解得:x=2或x=3.
【考点】解一元二次方程-因式分解法
【解析】【分析】(1)十字相乘法因式分解后求解即可得;(2)移项后提公因式法因式分解,再求解可得.