请选择
由于格式问题此试题可能会出现乱码的情况
为了方便您阅读请点击右上角的全屏查看
2018秦皇岛市中考数学模拟试题
一、精心选一选,慧眼识金!(本大题共14小题,每小题3分,共42分,在每小题给出的四个选项中只有一项是正确的)
1.化简![]() 的值是( )
的值是( )
A.﹣3 B.3 C.±3 D.9
2.下列等式不成立的是( )
A.6![]() •
•![]() =6
=6![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.下列二次根式中,最简二次根式的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.下列说法正确的是( )
A.若 a、b、c是△ABC的三边,则a2+b2=c2
B.若 a、b、c是Rt△ABC的三边,则a2+b2=c2
C.若 a、b、c是Rt△ABC的三边,∠A=90°,则a2+b2=c2
D.若 a、b、c是Rt△ABC的三边,∠C=90°,则a2+b2=c2
5.分别以下列四组数为一个三角形的边长:(1)3,4,5;(2)5,12,13;(3)8,15,17;(秦皇岛中考数学)(4)4,5,6.其中能构成直角三角形的有( )
A.4组 B.3组 C.2组 D.1组
6.将直线y=2x向上平移两个单位,所得的直线是( )
A.y=2x+2 B.y=2x﹣2 C.y=2(x﹣2) D.y=2(x+2)
7.一次函数y=x+1的图象在( )
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
8.小华的爷爷每天坚持体育锻炼,某天他漫步到离家较远的绿岛公园,打了一会儿太极拳后跑步回家.下面能反映当天小华的爷爷离家的距离y与时间x的函数关系的大致图象是( )
A.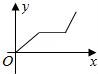 B.
B. C.
C.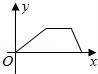 D.
D.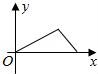
9.某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程(工作前洗衣机内无水),在这三个过程中洗衣机内水量y(升)与时间x(分)之间的函数关系对应的图象大致为( )
A.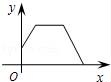 B.
B.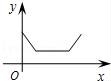 C.
C. D.
D.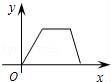
10.人数相同的八年级甲、乙两班学生在同一次数学单元测试,班级平均分和方差如下:![]() 甲=
甲=![]() 乙=80,s甲2=240,s乙2=180,则成绩较为稳定的班级是( )
乙=80,s甲2=240,s乙2=180,则成绩较为稳定的班级是( )
A.甲班 B.乙班
C.两班成绩一样稳定 D.无法确定
11.某地连续九天的最高气温统计如下表:
最高气温(℃) | 22 | 23 | 24 | 25 |
天数 | 1 | 2 | 2 | 4 |
则这组数据的中位数与众数分别是( )
A.24,25 B.24.5,25 C.25,24 D.23.5,24
12.顺次连接菱形各边中点所得的四边形一定是( )
A.等腰梯形 B.正方形 C.平行四边形 D.矩形
13.甲、乙两个准备在一段长为1200米的笔直公路上进行跑步,甲、乙跑步的速度分别为4m/s和6m/s,起跑前乙在起点,甲在乙前面100米处,若同时起跑,则两人从起跑至其中一人先到达终点的过程中,甲、乙两之间的距离y(m)与时间t(s)的函数图象是( )
A.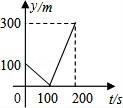 B.
B. C.
C. D.
D.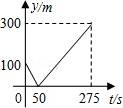
14.(秦皇岛中考数学)如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
A.1 B.![]() C.4﹣2
C.4﹣2![]() D.3
D.3![]() ﹣4
﹣4
二、填空题(简洁的结果,表达的是你敏锐的思维,需要的是细心!每小题3分,共18分)
15.已知一次函数y=kx+5的图象经过点(﹣1,2),则k= .
16.一名学生军训时连续射靶10次,命中的环数分别为4,7,8,6,8,5,9,10,7,6.则这名学生射击环数的方差是 .
17.直线y=kx+b与直线y=﹣2x+1平行,且经过点(﹣2,3),则kb= .
18.如图,OB,AB分别表示甲乙两名同学运动的一次函数图象,图中s与t分别表示运动路程和时间,已知甲的速度比乙快,下列说法:
①射线AB表示甲的路程与时间的函数关系;
②甲的速度比乙快1.5米/秒;
③甲比乙先跑12米;
④8秒钟后,甲超过了乙,
其中正确的有 .(填写你认为所有正确的答案序号)

19.如图,在周长为10cm的▱ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,则△ABE的周长为 .
20.(秦皇岛中考数学)如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为 .
三、解答题(耐心计算,认真推理,表露你萌动的智慧!共60分)
21.计算:![]()
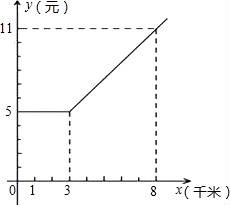
22.如图是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题:
(1)当行驶8千米时,收费应为 元;
(2)从图象上你能获得哪些信息(请写出2条);
① ;
② ;
(3)求出收费y(元)与行使x(千米)(x≥3)之间的函数关系式.
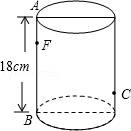
23.如图,圆柱形无盖玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm的点C处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口1cm的F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛所走的最短路线的长度.
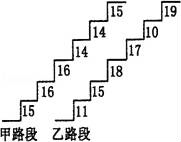
24.(秦皇岛中考数学)在某旅游景区上山的一条小路上,有一些断断续续的台阶.如图是其中的甲、乙段台阶路的示意图.请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服,为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
(图中的数字表示每一级台阶的高度(单位:cm).并且数据15,16,16,14,14,15的方差S甲2=![]() ,数据11,15,18,17,10,19的方差S乙2=
,数据11,15,18,17,10,19的方差S乙2=![]() ).
).
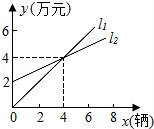
25.如图,l1表示神风摩托车厂一天的销售收入与摩托车销售量的关系;l2表示摩托车厂一天的销售成本与销售量的关系.
(1)写出销售收入与销售量之间的函数关系式;
(2)写出销售成本与销售量之间的函数关系式;
(3)当一天的销售量为多少辆时,销售收入等于销售成本;
(4)当一天的销售超过多少辆时,工厂才能获利?(利润=收入﹣成本)
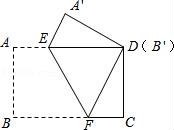
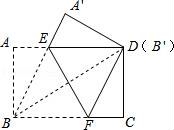
26.把一张矩形纸片ABCD按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=4cm.
(1)求线段DF的长;
(2)连接BE,求证:四边形BFDE是菱形;
(3)求线段EF的长.
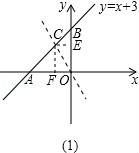
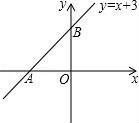
27.如图,已知直线y=x+3的图象与x、y轴交于A、B两点.直线l经过原点,与线段AB交于点C,把△AOB的面积分为2:1的两部分.求直线l的解析式.
秦皇岛中考数学参考答案与试题解析
一、精心选一选,慧眼识金!(本大题共14小题,每小题3分,共42分,在每小题给出的四个选项中只有一项是正确的)
1.化简![]() 的值是( )
的值是( )
A.﹣3 B.3 C.±3 D.9
【考点】73:二次根式的性质与化简.
【分析】由于![]() =|a|,由此即可化简求解.
=|a|,由此即可化简求解.
【解答】解:![]() =3.
=3.
故选B.
2.下列等式不成立的是( )
A.6![]() •
•![]() =6
=6![]() B.
B.![]() C.
C.![]() D.
D.![]()
【考点】79:二次根式的混合运算.
【分析】根据二次根式的混合运算依次计算,再进行选择即可.
【解答】解:A、6![]() •
•![]() =6
=6![]() ,故本选项成立;
,故本选项成立;
B、![]()
![]() =2,故本选项不成立;
=2,故本选项不成立;
C、![]() =
=![]() ,故本选项成立;
,故本选项成立;
D、![]() ﹣
﹣![]() =2
=2![]()
![]() =
=![]() ,故本选项成立.
,故本选项成立.
故选B.
3(秦皇岛中考数学).下列二次根式中,最简二次根式的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【考点】74:最简二次根式.
【分析】最简二次根式满足:(1)被开方数不含分母;(2)被开方数中不含能开得尽方的因数或因式,满足上述两个条件的二次根式,叫做最简二次根式.
【解答】解:A、![]() 中被开方数是分数,故不是最简二次根式;
中被开方数是分数,故不是最简二次根式;
B、![]() 中被开方数是分数,故不是最简二次根式;
中被开方数是分数,故不是最简二次根式;
C、![]() 中被开方数不含分母,不含能开得尽方的因数,故是最简二次根式;
中被开方数不含分母,不含能开得尽方的因数,故是最简二次根式;
D、![]() 中含能开得尽方的因数,故不是最简二次根式;
中含能开得尽方的因数,故不是最简二次根式;
故选:C
4.下列说法正确的是( )
A.若 a、b、c是△ABC的三边,则a2+b2=c2
B.若 a、b、c是Rt△ABC的三边,则a2+b2=c2
C.若 a、b、c是Rt△ABC的三边,∠A=90°,则a2+b2=c2
D.若 a、b、c是Rt△ABC的三边,∠C=90°,则a2+b2=c2
【考点】KQ:勾股定理.
【分析】根据勾股定理的使用范围和勾股定理进行判断.
【解答】解:A、若△ABC不是直角三角形,则a2+b2=c2不成立,故本选项错误;
B、若c不是Rt△ABC的斜边,则a2+b2=c2不成立,故本选项错误;
C、若 a、b、c是Rt△ABC的三边,∠A=90°,则c2+b2=a2,故本选项错误;
D、若 a、b、c是Rt△ABC的三边,∠C=90°,则a2+b2=c2,故本选项正确,
故选:D.
5.分别以下列四组数为一个三角形的边长:(1)3,4,5;(2)5,12,13;(3)8,15,17;(4)4,5,6.其中能构成直角三角形的有( )
A.4组 B.3组 C.2组 D.1组
【考点】KS:勾股定理的逆定理.
【分析】欲判断是否可以构成直角三角形,只需验证两小边的平方和是否等于最长边的平方.
【解答】解:(1)32+42=52,能构成直角三角形;
(2)52+122=132,能构成直角三角形;
(3)82+152=172,能构成直角三角形;
(4)52+42≠62,不能构成直角三角形;
则能构成直角三角形的有3组.
故选B.
6.将直线y=2x向上平移两个单位,所得的直线是( )
A.y=2x+2 B.y=2x﹣2 C.y=2(x﹣2) D.y=2(x+2)
【考点】F9:一次函数图象与几何变换.
【分析】平移时k的值不变,只有b发生变化.
【解答】解:原直线的k=2,b=0;向上平移两个单位得到了新直线,
那么新直线的k=2,b=0+2=2.
∴新直线的解析式为y=2x+2.
故选A.
7.(秦皇岛中考数学)一次函数y=x+1的图象在( )
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
【考点】F5:一次函数的性质.
【分析】在函数y=x+1中k=1>0,由此可以确定图象经过第一三象限,而b=1>0,图象过第二象限,所以可以确定直线y=x+1经过的象限.
【解答】解:∵k=1>0,
∴图象过一三象限,
∴b=1>0,图象过第二象限,
∴直线y=x+1经过第一、二、三象限.
故选A.
8.小华的爷爷每天坚持体育锻炼,某天他漫步到离家较远的绿岛公园,打了一会儿太极拳后跑步回家.下面能反映当天小华的爷爷离家的距离y与时间x的函数关系的大致图象是( )
A.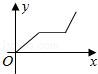 B.
B.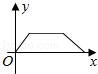 C.
C.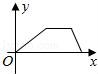 D.
D.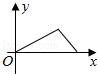
【考点】E6:函数的图象.
【分析】根据在每段中,离家的距离随时间的变化情况即可进行判断.
【解答】解:图象应分三个阶段,第一阶段:慢步到离家较远的绿岛公园,在这个阶段,离家的距离随时间的增大而增大;
第二阶段:打了一会儿太极拳,这一阶段离家的距离不随时间的变化而改变.故D错误;
第三阶段:跑步回家,这一阶段,离家的距离随时间的增大而减小,故A错误,并且这段的速度大于第一阶段的速度,则B错误.
故选:C.
9.某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程(工作前洗衣机内无水),在这三个过程中洗衣机内水量y(升)与时间x(分)之间的函数关系对应的图象大致为( )
A. B.
B. C.
C.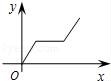 D.
D.
【考点】E6:函数的图象.
【分析】根据洗衣机内水量开始为0,清洗时水量不变,排水时水量变小,直到水量0,即可得到答案.
【解答】解:∵洗衣机工作前洗衣机内无水,
∴A,B两选项不正确,被淘汰;
又∵洗衣机最后排完水,
∴C选项不正确,被淘汰,
所以选项D正确.
故选:D.
10(秦皇岛中考数学).人数相同的八年级甲、乙两班学生在同一次数学单元测试,班级平均分和方差如下:![]() 甲=
甲=![]() 乙=80,s甲2=240,s乙2=180,则成绩较为稳定的班级是( )
乙=80,s甲2=240,s乙2=180,则成绩较为稳定的班级是( )
A.甲班 B.乙班
C.两班成绩一样稳定 D.无法确定
【考点】W7:方差.
【分析】根据方差的意义判断.方差越小,波动越小,越稳定.
【解答】解:∵s甲2>s乙2,
∴成绩较为稳定的班级是乙班.
故选B.
11.某地连续九天的最高气温统计如下表:
最高气温(℃) | 22 | 23 | 24 | 25 |
天数 | 1 | 2 | 2 | 4 |
则这组数据的中位数与众数分别是( )
A.24,25 B.24.5,25 C.25,24 D.23.5,24
【考点】W5:众数;W4:中位数.
【分析】根据众数和中位数的定义就可以求解.
【解答】解:在这一组数据中25是出现次数最多的,故众数是25;
处于这组数据中间位置的那个数是24,那么由中位数的定义可知,这组数据的中位数是24;
故这组数据的中位数与众数分别是24,25.
故选A.
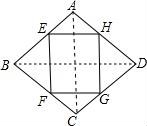
12.顺次连接菱形各边中点所得的四边形一定是( )
A.等腰梯形 B.正方形 C.平行四边形 D.矩形
【考点】LC:矩形的判定;KX:三角形中位线定理;L8:菱形的性质.
【分析】先证明四边形EFGH是平行四边形,再根据有一个角是直角的平行四边形是矩形判断.
【解答】解:如图:菱形ABCD中,E、F、G、H分别是AB、BC、CD、AD的中点,
∴EH∥FG∥BD,EH=FG=![]() BD;EF∥HG∥AC,EF=HG=
BD;EF∥HG∥AC,EF=HG=![]() AC,
AC,
故四边形EFGH是平行四边形,
又∵AC⊥BD,
∴EH⊥EF,∠HEF=90°
∴边形EFGH是矩形.
故选D.
13(秦皇岛中考数学).甲、乙两个准备在一段长为1200米的笔直公路上进行跑步,甲、乙跑步的速度分别为4m/s和6m/s,起跑前乙在起点,甲在乙前面100米处,若同时起跑,则两人从起跑至其中一人先到达终点的过程中,甲、乙两之间的距离y(m)与时间t(s)的函数图象是( )
A. B.
B.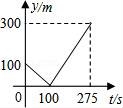 C.
C.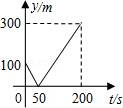 D.
D.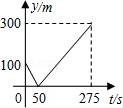
【考点】E6:函数的图象.
【分析】甲在乙前面,而乙的速度大于甲,则此过程为乙先追上甲后再超过甲,全程时间以乙跑的时间计算,算出相遇时间判断图象.
【解答】解:此过程可看作追及过程,由相遇到越来越远,按照等量关系“甲在相遇前跑的路程+100=乙在相遇前跑的路程”列出等式
v乙t=v甲t+100,根据
甲、乙跑步的速度分别为4m/s和6m/s,起跑前乙在起点,甲在乙前面100米处,
则乙要追上甲,所需时间为t=50,
全程乙跑完后计时结束t总=![]() =200,
=200,
则计时结束后甲乙的距离△s=(v乙﹣v甲)×(t总﹣t)=300m
由上述分析可看出,C选项函数图象符合
故选:C.
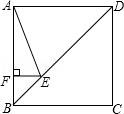
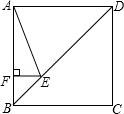
14.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
A.1 B.![]() C.4﹣2
C.4﹣2![]() D.3
D.3![]() ﹣4
﹣4
【考点】(秦皇岛中考数学)LE:正方形的性质.
【分析】根据正方形的对角线平分一组对角可得∠ABD=∠ADB=45°,再求出∠DAE的度数,根据三角形的内角和定理求∠AED,从而得到∠DAE=∠AED,再根据等角对等边的性质得到AD=DE,然后求出正方形的对角线BD,再求出BE,最后根据等腰直角三角形的直角边等于斜边的![]() 倍计算即可得解.
倍计算即可得解.
【解答】解:在正方形ABCD中,∠ABD=∠ADB=45°,
∵∠BAE=22.5°,
∴∠DAE=90°﹣∠BAE=90°﹣22.5°=67.5°,
在△ADE中,∠AED=180°﹣45°﹣67.5°=67.5°,
∴∠DAE=∠AED,
∴AD=DE=4,
∵正方形的边长为4,
∴BD=4![]() ,
,
∴BE=BD﹣DE=4![]() ﹣4,
﹣4,
∵EF⊥AB,∠ABD=45°,
∴△BEF是等腰直角三角形,
∴EF=![]() BE=
BE=![]() ×(4
×(4![]() ﹣4)=4﹣2
﹣4)=4﹣2![]() .
.
故选:C.
二、填空题(简洁的结果,表达的是你敏锐的思维,需要的是细心!每小题3分,共18分)
15.已知一次函数y=kx+5的图象经过点(﹣1,2),则k= 3 .
【考点】F8:一次函数图象上点的坐标特征.
【分析】直接把点(﹣1,2)代入一次函数y=kx+5,求出k的值即可.
【解答】解:∵一次函数y=kx+5的图象经过点(﹣1,2),
∴2=﹣k+5,解得k=3.
故答案为:3.
16.一名学生军训时连续射靶10次,命中的环数分别为4,7,8,6,8,5,9,10,7,6.则这名学生射击环数的方差是 3 .
【考点】W7:方差.
【分析】先计算数据的平均数后,再根据方差的公式计算.
【解答】解:数据4,7,8,6,8,5,9,10,7,6的平均数=![]() =7,
=7,
方差=![]() (9+4+1+9+4+1+1+4+9)=3.
(9+4+1+9+4+1+1+4+9)=3.
故填3.
17.(秦皇岛中考数学)直线y=kx+b与直线y=﹣2x+1平行,且经过点(﹣2,3),则kb= 2 .
【考点】FF:两条直线相交或平行问题.
【分析】由平行线的关系得出k=﹣2,再把点(﹣2,3)代入直线y=﹣2x+b,求出b,即可得出结果.
【解答】解:∵直线y=kx+b与直线y=﹣2x+1平行,
∴k=﹣2,
∴直线y=﹣2x+b,
把点(﹣2,3)代入得:4+b=3,
∴b=﹣1,
∴kb=2.
故答案为:2.
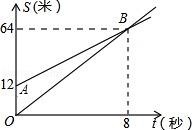
18.如图,OB,AB分别表示甲乙两名同学运动的一次函数图象,图中s与t分别表示运动路程和时间,已知甲的速度比乙快,下列说法:
①射线AB表示甲的路程与时间的函数关系;
②甲的速度比乙快1.5米/秒;
③甲比乙先跑12米;
④8秒钟后,甲超过了乙,
其中正确的有 ②③④ .(填写你认为所有正确的答案序号)
【考点】FH:一次函数的应用.
【分析】根据图形可以得出乙比甲先跑了12米,甲的速度比乙快1.5米/秒,8秒钟内,乙在甲前面,8秒钟后,甲超过了乙.
【解答】解:①射线AB表示乙的路程与时间的函数关系,故①错误;
②当t=8秒时,甲追上了乙,所以甲的速度比乙快12÷8=1.5米/秒,故②正确;
③由图形,t=0时,甲在乙前边12米,即甲让乙先跑12米,故③正确;
④8秒钟内,AB在OB的下面,即可知甲超过了乙,故④正确.
故答案为:②③④.
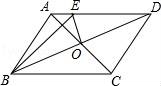
19.如图,在周长为10cm的▱ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,则△ABE的周长为 5cm .

【考点】L5:平行四边形的性质;KG:线段垂直平分线的性质.
【分析】先判断出EO是BD的中垂线,得出BE=ED,从而可得出△ABE的周长=AB+AD,再由平行四边形的周长为10cm,即可得出答案.
【解答】(秦皇岛中考数学)解:∵点O是BD中点,EO⊥BD,
∴EO是线段BD的中垂线,
∴BE=ED,
故可得△ABE的周长=AB+AD,
又∵平行四边形的周长为10cm,
∴AB+AD=5cm.
故答案为:5cm.
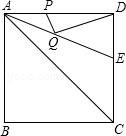
20.如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为 ![]() .
.
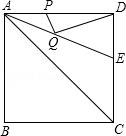
【考点】PA:轴对称﹣最短路线问题;LE:正方形的性质.
【分析】过D作AE的垂线交AE于F,交AC于D′,再过D′作D′P′⊥AD,由角平分线的性质可得出D′是D关于AE的对称点,进而可知D′P′即为DQ+PQ的最小值.
【解答】解:作D关于AE的对称点D′,再过D′作D′P′⊥AD于P′,
∵DD′⊥AE,
∴∠AFD=∠AFD′,
∵AF=AF,∠DAE=∠CAE,
∴△DAF≌△D′AF,
∴D′是D关于AE的对称点,AD′=AD=2,
∴D′P′即为DQ+PQ的最小值,
∵四边形ABCD是正方形,
∴∠DAD′=45°,
∴AP′=P′D′,
∴在Rt△AP′D′中,
P′D′2+AP′2=AD′2,AD′2=4,
∵AP′=P′D',
2P′D′2=AD′2,即2P′D′2=4,
∴P′D′=![]() ,即DQ+PQ的最小值为
,即DQ+PQ的最小值为![]() .
.
故答案为:![]() .
.
三、(秦皇岛中考数学)解答题(耐心计算,认真推理,表露你萌动的智慧!共60分)
21.计算:![]()
【考点】79:二次根式的混合运算.
【分析】先把各二次根式化为最简二次根式,再进行计算.
【解答】解:原式=3+2﹣![]() +
+![]() ﹣
﹣![]() =5﹣
=5﹣![]() .
.
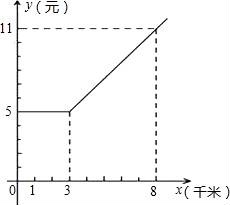
22.如图是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题:
(1)当行驶8千米时,收费应为 11 元;
(2)从图象上你能获得哪些信息(请写出2条);
① ①行驶路程小于或等于3千米时,收费是5元 ;
② ②超过3千米后每千米收费1.2元 ;
(3)求出收费y(元)与行使x(千米)(x≥3)之间的函数关系式.
【考点】FH:一次函数的应用.
【分析】(1)由图象即可确定行驶8千米时的收费;
(2)此题答案不唯一,只要合理就行;
(3)由于x≥3时,直线过点(3,5)、(8,11),设解析式为设y=kx+b,利用待定系数法即可确定解析式.
【解答】(秦皇岛中考数学)解:(1)当行驶8千米时,收费应为11元;
(2)①行驶路程小于或等于3千米时,收费是5元;
②超过3千米后每千米收费1.2元;
(3)由于x≥3时,直线过点(3,5)、(8,11),
设解析式为设y=kx+b,
则![]() ,
,
解得k=1.2,b=1.4,
则解析式为y=1.2x+1.4.
23.如图,圆柱形无盖玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm的点C处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口1cm的F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛所走的最短路线的长度.
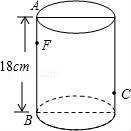
【考点】KV:平面展开﹣最短路径问题.
【分析】要求不在同一个平面内的两点之间的最短距离,首先要把两个点展开到一个平面内,然后分析展开图形中的数据,根据勾股定理即可求解.
【解答】解:将曲面沿AB展开,如图所示,过C作CE⊥AB于E,
在Rt△CEF中,∠CEF=90°,EF=18﹣1﹣1=16(cm),CE=![]() ×60=30(cm),
×60=30(cm),
由勾股定理,得CF=![]() =34(cm).
=34(cm).
答:蜘蛛所走的最短路线是34cm.

24.(秦皇岛中考数学)在某旅游景区上山的一条小路上,有一些断断续续的台阶.如图是其中的甲、乙段台阶路的示意图.请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服,为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
(图中的数字表示每一级台阶的高度(单位:cm).并且数据15,16,16,14,14,15的方差S甲2=![]() ,数据11,15,18,17,10,19的方差S乙2=
,数据11,15,18,17,10,19的方差S乙2=![]() ).
).
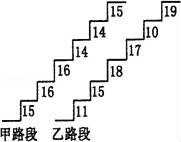
【考点】W7:方差;W1:算术平均数;W4:中位数;W6:极差.
【分析】(1)分别求出甲、乙的中位数、方差和极差进而分析得出即可;
(2)根据方差的性质得出即可;
(3)根据方差的稳定性得出即可.
【解答】解:(1)∵从小到大排列出台阶的高度值:甲的,14,14,15,15,16,16,乙的,10,11,15,17,18,19,
甲的中位数、方差和极差分别为,15cm;![]() ;16﹣14=2(cm),
;16﹣14=2(cm),
乙的中位数、方差和极差分别为,(15+17)÷2=16(cm),![]() ,19﹣10=9(cm)
,19﹣10=9(cm)
平均数:![]() (15+16+16+14+14+15)=15(cm);
(15+16+16+14+14+15)=15(cm);
∴![]() (11+15+18+17+10+19)=15(cm).
(11+15+18+17+10+19)=15(cm).
∴相同点:两段台阶路高度的平均数相同.
不同点:两段台阶路高度的中位数、方差和极差均不相同.
(2)甲路段走起来更舒服一些,因为它的台阶高度的方差小.
(3)每个台阶高度均为15cm(原平均数),使得方差为0.
25.如图,l1表示神风摩托车厂一天的销售收入与摩托车销售量的关系;l2表示摩托车厂一天的销售成本与销售量的关系.
(1)写出销售收入与销售量之间的函数关系式;
(2)写出销售成本与销售量之间的函数关系式;
(3)当一天的销售量为多少辆时,销售收入等于销售成本;
(4)当一天的销售超过多少辆时,工厂才能获利?(利润=收入﹣成本)
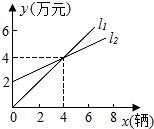
【考点】FH:一次函数的应用.
【分析】(秦皇岛中考数学)(1)设y=kx,根据题意可知当x=4时,y=4,则k=1,即销售收入与销售量之间的函数关系式为y=x;
(2)设y=kx+b,把已知坐标代入可得解析式y=![]() x+2;
x+2;
(3)由图可知当x=4时,销售收入等于销售成本,故x=4;
(4)由图象可知x>4时,工厂才能获利.
【解答】解:(1)设y=kx,
∵直线过(4,4)两点,
∴4=4k,
∴k=1,
∴y=x;
(2)设y=kx+b,
∵直线过(0,2)、(4,4)两点,
∴2=b,4=4k+2,
∴k=![]() ,
,
∴y=![]() x+2;
x+2;
(3)由图象知,当x=4时,销售收入等于销售成本,
∴x=![]() x+2,
x+2,
∴x=4;
(4)由图象知:当x>4时,工厂才能获利,
或x﹣(![]() x+2)>0时,即x>4时,才能获利.
x+2)>0时,即x>4时,才能获利.
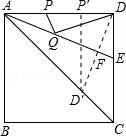
26.把一张矩形纸片ABCD按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=4cm.
(1)求线段DF的长;
(2)连接BE,求证:四边形BFDE是菱形;
(3)求线段EF的长.
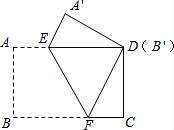
【考点】PB:翻折变换(折叠问题).
【分析】(1)根据折叠的性质知:BF=DF.在Rt△DCF中,利用勾股定理可求得DF的长;
(2)证得DE=DF,得四边形BFDE是平行四边形,得四边形BFDE是菱形;
(3)连接BD,得BD=5cm,利用![]() ,易得EF的长.
,易得EF的长.
【解答】(秦皇岛中考数学)解:(1)由折叠知,BF=DF.
在Rt△DCF中,DF2=(4﹣DF)2+32,
解得DF=![]() cm;
cm;
(2)由折叠的性质可得∠BFE=∠DFE,
∵AD∥BC,
∴∠BFE=∠DEF,
∴∠DFE=∠DEF,
∴DE=DF,
∴四边形BFDE是平行四边形,
∴四边形BFDE是菱形;
(3)连接BD.
在Rt△BCD中,BD=![]() =5,
=5,
∵![]() ,
,
∴![]() EF×5=
EF×5=![]() ×3
×3
解得EF=![]() cm.
cm.
27.如图,已知直线y=x+3的图象与x、y轴交于A、B两点.直线l经过原点,与线段AB交于点C,把△AOB的面积分为2:1的两部分.求直线l的解析式.

【考点】FA:待定系数法求一次函数解析式.
【分析】根据直线y=x+3的解析式可求出A、B两点的坐标,如图:
(1)当直线l把△ABO的面积分为S△AOC:S△BOC=2:1时,作CF⊥OA于F,CE⊥OB于E,可分别求出△AOB与△AOC的面积,再根据其面积公式可求出两直线交点的坐标,从而求出其解析式;
(2)当直线l把△ABO的面积分为S△AOC:S△BOC=1:2时,同(1).
【解答】(秦皇岛中考数学)解:由直线y=x+3的解析式可求得A(﹣3,O)、B(0,3),
如图(1),当直线l把△ABO的面积分为S△AOC:S△BOC=2:1时,
作CF⊥OA于F,CE⊥OB于E,则S△AOB=![]() ,则S△AOC=3,
,则S△AOC=3,
∴![]() AO•CF=3,即
AO•CF=3,即![]() ×3×CF=3
×3×CF=3
∴CF=2同理,解得CE=1.
∴C(﹣1,2),
∴直线l的解析式为y=﹣2x;
如图(2),当直线l把△ABO的面积分为S△AOC:S△BOC=1:2时
同理求得C(﹣2,1),
∴直线l的解析式为y=﹣![]() (求C点的坐标时亦可用相似的知识求得).
(求C点的坐标时亦可用相似的知识求得).