2018石家庄市中考数学模拟试题【解析版含答案】

由于格式问题此试题可能会出现乱码的情况

为了方便您阅读请点击右上角的全屏查看

2018石家庄市中考数学模拟试题

一、精心选一选（每小题4分，共40分）

1．如图，在平行四边形ABCD中，CE⊥AB且E为垂足．如果∠A=125°，则∠BCE=（　　）

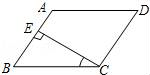
A．55°              B．35°              C．25°              D．30°

2．已知a⊥b，b∥c，则直线a和直线c的关系为（　　）

A．相交              B．垂直              C．平行              D．以上都不对

3．已知一次函数y=kx+b的图象经过一、二、四象限，则下列判断正确的是（　　）

A．k＞0，b＞0              B．k＜0，b＜0              C．k＞0，b＜0              D．k＜0，b＞0

4．若一个多边形的内角和为1080°，则这个多边形的边数为（　　）

A．6              B．7              C．8              D．9

5．一组数据20，20，50，20，37，2，把2换成其他的任意数，不改变的是（　　）

A．众数              B．平均数              C．中位数              D．众数和中位数

6．如果函数y=ax+b（a＜0，b＜0）和y=kx（k＞0）的图象交于点P，那么点P应该位于（　　）

A．第一象限              B．第二象限              C．第三象限              D．第四象限

7．（石家庄中考数学）如图，AB∥CD，那么∠A+∠C+∠AEC=（　　）

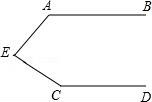
A．360°              B．270°              C．200°              D．180°

8．人数相等的甲、乙两班学生参加同一次数学测验，班级平均分和方差如下： =80， =80，x甲2=240，x乙2=100，则成绩较为整齐的是（　　）

A．甲班              B．乙班              C．两班一样整齐              D．无法确定

9．某校八年级同学到距学校6千米的郊外春游，一部分同学步行，另一部分同学骑自行车，沿相同路线前往．如图，a，b分别表示步行和骑车的同学前往目的地所走的路程y（千米）与所用时间x（分钟）之间的函数图象，则下列判断错误的是（　　）

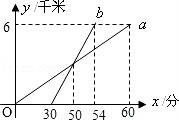
A．骑车的同学比步行的同学晚出发30分钟

B．步行的速度是6千米/小时

C．骑车的同学从出发到追上步行的同学用了20分钟

D．骑车的同学和步行的同学同时到达目的地

10．炎炎夏日，甲安装队为A小区安装66台空调，乙安装队为B小区安装60台空调，两队同时开工且恰好同时完工，甲队比乙队每天多安装2台．设乙队每天安装x台，根据题意，下面所列方程中正确的是（　　）

A．              B．              C．              D．

二、耐心填一填（每小题4分，共40分）

11．命题“直角三角形两个锐角互余”的条件是　   　，结论是　   　．

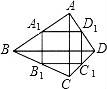
12．如图，四边形ABCD的两条对角线AC，BD互相垂直，A1，B1，C1，D1是四边形ABCD的中点四边形，如果AC=8，BD=10，那么四边形A1B1C1D1的面积为　   　．

13．一次函数y=x﹣1的图象不经过第　   　象限，并且y随x的　   　而增大．

14．一个正方形的边长为10厘米，它的边长减少x厘米后，得到的新正方形的周长为y厘米，则y与x之间的函数关系式为　   　．

15．一次函数y=kx+b，当x=﹣4时，y=9；当x=2时，y=3；当x=1时，y=　   　．

16．（石家庄中考数学）已知一次函数y=ax+b（a、b为常数），x与y的部分对应值如右表：

那么方程ax+b=0的解是　   　，不等式ax+b＞0的解是　   　．

17．已知数据x1，x2，…，xn的平均数是，则数据x1+8，x2+8，…，xn+8的平均数是　   　．

18．如图，梯形ABCD中，AB∥CD，AD=CD，E、F分别是AB、BC的中点，若∠1=35°，则∠D=　   　度．

19．某公司有10名销售员，去年完成销售额情况如下表：

已知销售额的平均数为5.6万元，众数为4万元，中位数为5万元．今年公司为了调动员工的积极性，提高年销售额，准备采取超额有奖的措施，根据以上信息，确定　   　万元为销售额标准．

20．直角三角形两直角边的垂直平分线交于点P，则P点在　   　（填点P的位置）．

三、解答题（每题10分）

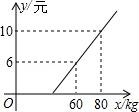
21．长途汽车客运公司规定旅客可随身携带一定重量的行李，如果超过规定，则需要购买行李票，行李票费用y（元）是行李重量x（千克）的一次函数，其图象如图7所示．求出y与x之间的函数关系式，并说明行李的重量不超过多少千克，就可以免费托运？

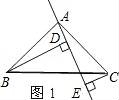
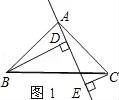
22．（1）如图1，△ABC中，∠BAC=90°，AB=AC，AE是过A点的一条直线，且B、C在AE的异侧，BD⊥AE于D，CE⊥AE于E，求证：BD=DE+CE．

（2）若直线AE绕点A旋转到图2的位置时（BD＜CE），其余条件不变，问BD与DE、CE的关系如何？请予以证明．

　石家庄中考数学参考答案与试题解析

一、精心选一选（每小题4分，共40分）

1．如图，在平行四边形ABCD中，CE⊥AB且E为垂足．如果∠A=125°，则∠BCE=（　　）

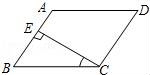
A．55°              B．35°              C．25°              D．30°

【考点】L5：平行四边形的性质．

【分析】根据平行四边形性质及直角三角形的角的关系，即可求解．

【解答】解：∵平行四边形ABCD

∴AD∥BC，

∴∠B=180°﹣∠A=55°，

又∵CE⊥AB，

∴∠BCE=35°．

故选B．

2．已知a⊥b，b∥c，则直线a和直线c的关系为（　　）

A．相交              B．垂直              C．平行              D．以上都不对

【考点】JA：平行线的性质；J3：垂线．

【分析】如果一条直线和一组平行线中的一条垂直，那么和其他直线也垂直．

【解答】解：∵a⊥b，b∥c，

∴a⊥c

故选B．

3．已知一次函数y=kx+b的图象经过一、二、四象限，则下列判断正确的是（　　）

A．k＞0，b＞0              B．k＜0，b＜0              C．k＞0，b＜0              D．k＜0，b＞0

【考点】F7：一次函数图象与系数的关系．

【分析】根据图象在坐标平面内的位置确定k，b的取值范围．

【解答】解：∵一次函数y=kx+b的图象经过第一、二、四象限，

∴k＜0，b＞0．

故选D．

4．若一个多边形的内角和为1080°，则这个多边形的边数为（　　）

A．6              B．7              C．8              D．9

【考点】L3：多边形内角与外角．

【分析】首先设这个多边形的边数为n，由n边形的内角和等于180°（n﹣2），即可得方程180（n﹣2）=1080，解此方程即可求得答案．

【解答】解：设这个多边形的边数为n，

根据题意得：180（n﹣2）=1080，

解得：n=8．

故选C．

5．（石家庄中考数学）一组数据20，20，50，20，37，2，把2换成其他的任意数，不改变的是（　　）

A．众数              B．平均数              C．中位数              D．众数和中位数

【考点】W5：众数．

【分析】众数就是出现次数最多的数，把2换成其他的任意数，20出现的次数都最多，因而不改变的是众数；2改变，根据平均数的计算方法，数的和一定改变，因而平均数一定会变；2变化的不同，这几个数的大小顺序一定会改变，因而中位数也一定改变．

【解答】解：由于20已经出现三次，一定是众数，故不改变的是众数．

故选A．

6．如果函数y=ax+b（a＜0，b＜0）和y=kx（k＞0）的图象交于点P，那么点P应该位于（　　）

A．第一象限              B．第二象限              C．第三象限              D．第四象限

【考点】FF：两条直线相交或平行问题．

【分析】根据a、b的取值，判断出一次函数所过的象限，再根据k的取值，判断出正比例函数所过的象限，二者所过的公共象限即为点P所在象限．

【解答】解：∵函数y=ax+b（a＜0，b＜0）的图象经过第二、三、四象限，

y=kx（k＞0）的图象过原点、第一、三象限，

∴点P应该位于第三象限．

故选C．

7．如图，AB∥CD，那么∠A+∠C+∠AEC=（　　）

A．360°              B．270°              C．200°              D．180°

【考点】JA：平行线的性质．

【分析】过点E作EF∥AB，根据平行线的性质，∠A+∠C+∠AEC就可以转化为两对同旁内角的和．

【解答】解：过点E作EF∥AB，

∴∠A+∠AEF=180°；

∵AB∥CD，

∴EF∥CD，

∴∠C+∠FEC=180°，

∴（∠A+∠AEF）+（∠C+∠FEC）=360°，

即：∠A+∠C+∠AEC=360°．

故选A．

8．（石家庄中考数学）人数相等的甲、乙两班学生参加同一次数学测验，班级平均分和方差如下： =80， =80，x甲2=240，x乙2=100，则成绩较为整齐的是（　　）

A．甲班              B．乙班              C．两班一样整齐              D．无法确定

【考点】W7：方差．

【分析】根据方差的定义，方差越小数据越稳定．

【解答】解：∵=80， =80，S甲2=240，S乙2=100分，

∴S甲2＞S乙2，

∴成绩较为整齐的是乙班；

故选B．

9．某校八年级同学到距学校6千米的郊外春游，一部分同学步行，另一部分同学骑自行车，沿相同路线前往．如图，a，b分别表示步行和骑车的同学前往目的地所走的路程y（千米）与所用时间x（分钟）之间的函数图象，则下列判断错误的是（　　）

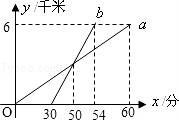
A．骑车的同学比步行的同学晚出发30分钟

B．步行的速度是6千米/小时

C．骑车的同学从出发到追上步行的同学用了20分钟

D．骑车的同学和步行的同学同时到达目的地

【考点】E6：函数的图象．

【分析】根据图象上特殊点的坐标和实际意义即可求出答案．

【解答】解：骑车的同学比步行的同学晚出发30分钟，所以A正确；

步行的速度是6÷1=6千米/小时，所以B正确；

骑车的同学从出发到追上步行的同学用了50﹣30=20分钟，所以C正确；

骑车的同学用了54﹣30=24分钟到目的地，比步行的同学提前6分钟到达目的地，

故选D．

10．（石家庄中考数学）炎炎夏日，甲安装队为A小区安装66台空调，乙安装队为B小区安装60台空调，两队同时开工且恰好同时完工，甲队比乙队每天多安装2台．设乙队每天安装x台，根据题意，下面所列方程中正确的是（　　）

A．              B．              C．              D．

【考点】B6：由实际问题抽象出分式方程．

【分析】关键描述语为：“两队同时开工且恰好同时完工”，那么等量关系为：甲队所用时间=乙队所用时间．

【解答】解：乙队用的天数为：，甲队用的天数为：．

则所列方程为：．

故选：D．

二、耐心填一填（每小题4分，共40分）

11．命题“直角三角形两个锐角互余”的条件是　一个直角三角形中的两个锐角　，结论是　这两个锐角互余　．

【考点】O1：命题与定理．

【分析】命题有条件和结论两部分组成，条件是已知的，结论是结果．

【解答】解：“直角三角形两个锐角互余”的条件是一个直角三角形中的两个锐角，结论是这两个锐角互余．

12．如图，四边形ABCD的两条对角线AC，BD互相垂直，A1，B1，C1，D1是四边形ABCD的中点四边形，如果AC=8，BD=10，那么四边形A1B1C1D1的面积为　20　．

【考点】KX：三角形中位线定理；LB：矩形的性质；LL：梯形中位线定理．

【分析】此题要能够根据三角形的中位线定理证明四边形A1B1C1D1是矩形，从而根据矩形的面积进行计算．

【解答】解：∵A1，B1，C1，D1是四边形ABCD的中点四边形，且AC=8，BD=10

∴A1D1是△ABD的中位线

∴A1D1=BD=×10=5

同理可得A1B1=AC=4

根据三角形的中位线定理，可以证明四边形A1B1C1D1是矩形

那么四边形A1B1C1D1的面积为A1D1×A1B1=5×4=20．

13．一次函数y=x﹣1的图象不经过第　二　象限，并且y随x的　增大　而增大．

【考点】F5：一次函数的性质．

【分析】根据k，b的符号判断一次函数经过的象限．

【解答】解：∵k=1＞0，b=﹣1＜0，∴图象过第一三四象限，不经过第二象限，且y随x的增大而增大．

14．一个正方形的边长为10厘米，它的边长减少x厘米后，得到的新正方形的周长为y厘米，则y与x之间的函数关系式为　y=40﹣4x　．

【考点】FG：根据实际问题列一次函数关系式．

【分析】此题根据新正方形的周长=新边长×4=（原边长﹣减少的长度）×4即可列出函数关系式．

【解答】解：依题意有：y=（10﹣x）×4=40﹣4x，

故y与x之间的函数关系式为：y=40﹣4x．

15．（石家庄中考数学）一次函数y=kx+b，当x=﹣4时，y=9；当x=2时，y=3；当x=1时，y=　4　．

【考点】FA：待定系数法求一次函数解析式．

【分析】当x=﹣4时，y=9；当x=2时，y=3代入求出一次函数，再将x=1代入求出y的值．

【解答】解：当x=﹣4时，y=9；

当x=2时，y=3；

代入一次函数y=kx+b得到，

解得，

则一次函数解析式为y=﹣x+5，

把x=1代入y=﹣x+5得y=4．

故填4．

16．已知一次函数y=ax+b（a、b为常数），x与y的部分对应值如右表：

那么方程ax+b=0的解是　x=1　，不等式ax+b＞0的解是　x＜1　．

【考点】FC：一次函数与一元一次方程；FD：一次函数与一元一次不等式．

【分析】方程ax+b=0的解为y=0时函数y=ax+b的x的值，根据图表即可得出此方程的解．

不等式ax+b＞0的解集为函数y=ax+b中y＞0时自变量x的取值范围，由图表可知，y随x的增大而减小，因此x＜1时，函数值y＞0；即不等式ax+b＞0的解为x＜1．

【解答】解：根据图表可得：当x=1时，y=0；

因而方程ax+b=0的解是x=1；

y随x的增大而减小，因而不等式ax+b＞0的解是：x＜1．

故答案为：x=1；x＜1．

17．已知数据x1，x2，…，xn的平均数是，则数据x1+8，x2+8，…，xn+8的平均数是　+8　．

【考点】W1：算术平均数．

【分析】根据数据x1，x2，…，xn的平均数为=（x1+x2+…+xn），即可求出数据x1+8，x2+8，…，xn+8的平均数．

【解答】解：数据x1+8，x2+8，…，xn+8的平均数=（x1+8+x2+8+…+xn+8）=（x1+x2+…+xn）+8=+8．

故答案为+8．

18．（石家庄中考数学）如图，梯形ABCD中，AB∥CD，AD=CD，E、F分别是AB、BC的中点，若∠1=35°，则∠D=　110　度．

【考点】LH：梯形．

【分析】先根据平行线的性质和AD=CD求出∠DAC与∠DCA都等于∠1的度数，再根据三角形内角和定理即可求出．

【解答】解：∵梯形ABCD中，AB∥CD

∴∠DCA=∠CAB

∵AD=CD

∴∠DCA=∠DAC

又∵E、F分别是AB、BC的中点

∴EF∥AC，∠1=∠CAB=∠DCA=∠DAC=35°

在△ADC中，∠DCA=∠DAC=35°

∴∠D=180°﹣∠DCA﹣∠DAC

=180°﹣35°﹣35°

=110°

故应填110．

19．某公司有10名销售员，去年完成销售额情况如下表：

已知销售额的平均数为5.6万元，众数为4万元，中位数为5万元．今年公司为了调动员工的积极性，提高年销售额，准备采取超额有奖的措施，根据以上信息，确定　5　万元为销售额标准．

【考点】W4：中位数；W1：算术平均数；W5：众数．

【分析】平均数是指在一组数据中所有数据之和再除以数据的个数．

众数是一组数据中出现次数最多的数；

中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数．

【解答】解：根据以上信息，根据中位数的意义，确定中位数为销售额标准．

即确定5万元为销售额标准．

故填5．

20．直角三角形两直角边的垂直平分线交于点P，则P点在　斜边中点　（填点P的位置）．

【考点】KG：线段垂直平分线的性质；KN：直角三角形的性质．

【分析】利用三角形中位线的性质和直角三角形的性质判断．

【解答】解：三角形ABC中，∠C=90°

作BC垂直平分线EF，交BC于F，交AB于E

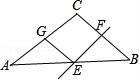
因为AC垂直BC，EF垂直于BC

所以AC平行EF，又因为F是BC的中点

所以E是AB的中点

过E作EG垂直AB于G

显然，G是AC的中点，所以EG是AC的垂直平分线

所以直角三角形两直角边的垂直平分线交于斜边的中点．

故填P点在斜边中点．

三、（石家庄中考数学）解答题（每题10分）

21．长途汽车客运公司规定旅客可随身携带一定重量的行李，如果超过规定，则需要购买行李票，行李票费用y（元）是行李重量x（千克）的一次函数，其图象如图7所示．求出y与x之间的函数关系式，并说明行李的重量不超过多少千克，就可以免费托运？

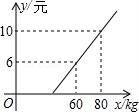
【考点】FH：一次函数的应用．

【分析】观察函数图象找出两点的坐标，利用待定系数法即可求出y与x之间的函数关系式，再代入y=0求出x值即可得出结论．

【解答】解：设y与x之间的函数关系式为y=kx+b（k≠0），

将（60，6）、（80，10）代入y=kx+b中，

，解得：，

∴y与x之间的函数关系式为y=0.2x﹣6．

当y=0，即0.2x﹣6=0时，x=30，

∴当行李的重量不超过30千克时，就可以免费托运．

22．（石家庄中考数学）（1）如图1，△ABC中，∠BAC=90°，AB=AC，AE是过A点的一条直线，且B、C在AE的异侧，BD⊥AE于D，CE⊥AE于E，求证：BD=DE+CE．

（2）若直线AE绕点A旋转到图2的位置时（BD＜CE），其余条件不变，问BD与DE、CE的关系如何？请予以证明．

【考点】KC：直角三角形全等的判定；KA：全等三角形的性质．

【分析】根据已知利用AAS判定△ABD≌△CAE从而得到BD=AE，AD=CE，因为AE=AD+DE，所以BD=DE+CE；

根据已知利用AAS判定△ABD≌△CAE从而得到BD=AE，AD=CE，因为AD+AE=BD+CE，所以BD=DE﹣CE．

【解答】解：（1）∵∠BAC=90°，BD⊥AE，CE⊥AE，

∴∠BDA=∠AEC=90°，

∵∠ABD+∠BAE=90°，∠CAE+∠BAE=90°

∴∠ABD=∠CAE，

∵AB=AC，

在△ABD和△CAE中，

∵，

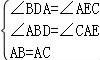∴△ABD≌△CAE（AAS），

∴BD=AE，AD=CE，

∵AE=AD+DE，

∴BD=DE+CE；

（2）BD=DE﹣CE；

∵∠BAC=90°，BD⊥AE，CE⊥AE，

∴∠BDA=∠AEC=90°，

∴∠ABD+∠DAB=∠DAB+∠CAE，

∴∠ABD=∠CAE，

∵AB=AC，

在△ABD和△CAE中，

∵，

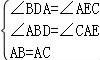∴△ABD≌△CAE（AAS），

∴BD=AE，AD=CE，

∴AD+AE=BD+CE，

∵DE=BD+CE，

∴BD=DE﹣CE．

第1页（共16页）