请选择
2018年河北中考数学模拟冲刺试题【Word版】
注意:由于格式问题,部分试题考生在预览时会出现乱码情况,如有此现象发生,请点击全屏查看。
(考试时间:120分钟 试卷满分:120分)
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
5.考试范围:中考全部内容。
第Ⅰ卷
一、选择题(本大题共16小题,共42分,1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)
1.在–(–5),–(–5)2,–|–5|,(–5)3中正数有
A.1个 B.2个
C.3个 D.4个
2.“嫦娥一号”卫星顺利进入绕月工作轨道,行程约有1800000千米,1800000这个数用科学记数法可以表示为
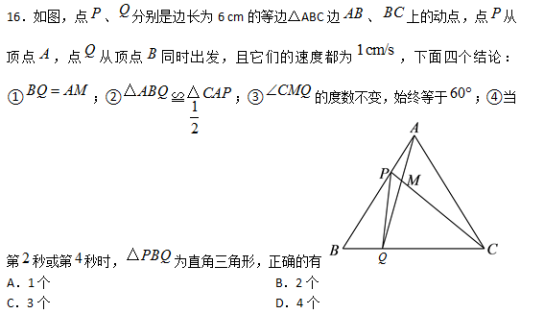
A.0.18×107 B.1.8×105
C.1.8×106 D.18×105
3.下列图形中,是轴对称图形,但不是中心对称图形的是
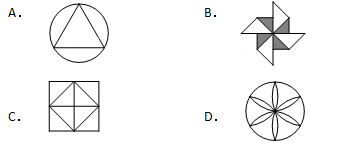
4.计算–12a6÷3a2的结果是
A.–4a3 B.–4a8
C.–4a4 D.– a4
5.下列图形中,∠2>∠1的是
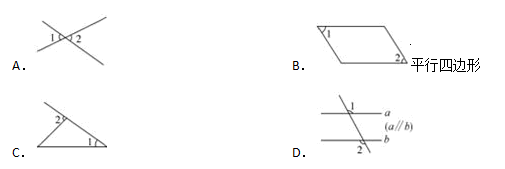
6.如图是一个几何体的三视图,则这个几何体是
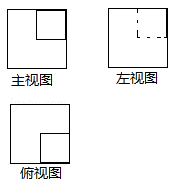
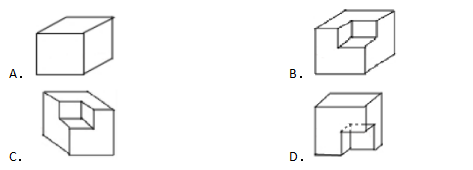

8.在某校开展的“书香校园”读书活动中,学校为了解八年级学生的读书情况,随机调查了八年级50名学生每学期每人读书的册数,绘制统计表如下:
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 4 | 12 | 16 | 17 | 1 |
则这50个样本数据的众数和中位数分别是
A.17,16 B.3,2.5
C.2,3 D.3,2
9.如图所示,AB∥CD,P为AB,CD之间的一点,已知∠1=32°,∠2=25°,∠BPC的度数为
A.57° B.47°
C.58° D.42°
10.如图,矩形ABCD的边AB=1,BE平分∠ABC,交AD于点E,若点E是AD的中点,以点B为圆心,BE为半径画弧,交BC于点F,则图中阴影部分的面积是


11.如图,小明从A处出发沿北偏西30°方向行走至B处,又沿南偏西50°方向行走至C处,此时再沿与出发时一致的方向行走至D处,则∠BCD的度数为
A.100° B.80°
C.50° D.20°
12.我们知道,溶液的酸碱度由PH确定.当PH>7时,溶液呈碱性;当PH<7时,溶液呈酸性.若将给定的HCl溶液加水稀释,那么在下列图象中,能反映HCl溶液的PH与所加水的体积(V)的变化关系的是
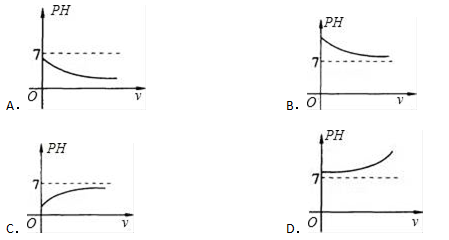
13.八年级学生去距学校10 km的博物馆参观,一部分学生骑自行车先走,过了20 min后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.设骑车学生的速度为x km/h,则所列方程正确的是


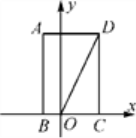
15.如图,矩形ABCD的边BC在x轴上,点A在第二象限,点D在第一象限,AB=2![]() ,OD=4,将矩形ABCD绕点O旋转,使点D落在x轴上,则点C对应点的坐标是
,OD=4,将矩形ABCD绕点O旋转,使点D落在x轴上,则点C对应点的坐标是

第Ⅱ卷
二、填空题(本大题共3小题,共10分.17~18小题各3分;19小题有两个空,每空2分)
17.若a与2a−9互为相反数,则a的值为__________.
18.如图,在已知的△ABC中,按以下步骤作图:
①分别以B,C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.
若CD=AC,∠A=50°,则∠ACB=__________.

19.如图,用黑白两种颜色的纸片,按黑色纸片数逐渐增加1的规律拼成如图图案,则第4个图案中有__________白色纸片,第n个图案中有__________张白色纸片.

三、解答题(本大题共7小题,共68分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分8分)数学课上,老师出了一道题:化简[8(a+b)5–4(a+b)4+(–a–b)3]÷[2(a+b)3].
小明同学马上举手,下面是小明的解题过程:
[8(a+b)5–4(a+b)4+(–a–b)3]÷[2(a+b)3]
=[8(a+b)5–4(a+b)4+(a+b)3]÷8(a+b)3
![]()
![]()
=(a+b)2– (a+b)+ .
小亮也举起了手,说小明的解题过程不对,并指了出来.老师肯定了小亮的回答.你知道小明错在哪儿吗?请指出来,并写出正确解答.
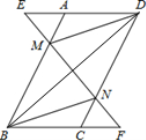
21.(本小题满分9分)如图所示,在平行四边形ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
(1)求证:△AEM≌△CFN;
(2)求证:BD与MN互相平分.
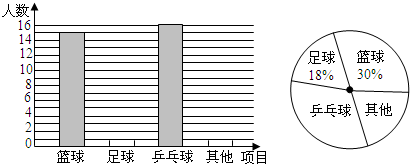
22.(本小题满分9分)在大课间活动中,同学们积极参加体育锻炼,小明就本班同学“我最喜爱的体育项目”进行了一次调查统计,下面是他通过收集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(1)该班共有__________名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“乒乓球”部分所对应的圆心角度数为__________;
(4)学校将举办体育节,该班将推选5位同学参加乒乓球活动,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.
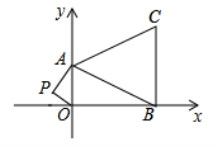
23.(本小题满分9分)如图,在平面直角坐标系中,已知点A(0,4),B(8,0),C(8,6)三点.
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点的坐标.
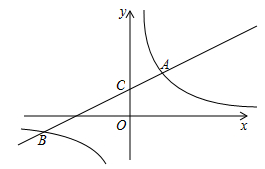
24.(本小题满分10分)如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双
![]()
曲线y= 相交于点A(m,6)和点B(–3,n),直线AB与y轴交于点C.
(1)求直线AB的表达式;
(2)求AC∶CB的值.
25.(本小题满分11分)已知在矩形ABCD中,AB=2,AD=4.P是对角线BD上的一个动点(点P不与点B、D重合),过点P作PF⊥BD,交射线BC于点F.连接AP,画∠FPE=∠BAP,PE交BF于点E.设PD=x,EF=y.
(1)当点A、P、F在一条直线上时,求△ABF的面积;
(2)如图1,当点F在边BC上时,求y关于x的函数解析式,并写出函数定义域;
(3)连接PC,若∠FPC=∠BPE,请直接写出PD的长.
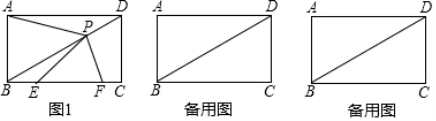
26.(本小题满分12分)定义:如图1,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,点P在该抛物线上(点P与A、B两点不重合),如果△ABP的三边满足AP2+BP2=AB2,则称点P为抛物线y=ax2+bx+c(a≠0)的勾股点.
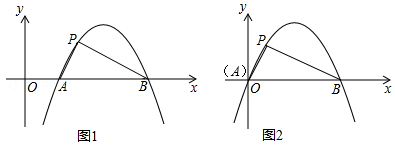
(1)直接写出抛物线y=–x2+1的勾股点的坐标;
(2)如图2,已知抛物线C:y=ax2+bx(a≠0)与x轴交于A,B两点,点P(1,![]() )是抛物线C的勾股点,求抛物线C的函数表达式;
)是抛物线C的勾股点,求抛物线C的函数表达式;
(3)在(2)的条件下,点Q在抛物线C上,求满足条件S△ABQ=S△ABP的Q点(异于点P)的坐标.