请选择
![]() 2018年泰安中考数学冲刺试卷【精选word版】
2018年泰安中考数学冲刺试卷【精选word版】
由于格式问题,部分试题会存在乱码的现象,请考生点击全屏查看!
一、选择题
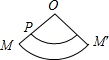
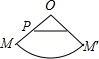
1.已知O为圆锥的顶点,M为圆锥底面上一点,点P在OM上.一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如图所示.若沿OM将圆锥侧面剪开并展开,所得侧面展开图是( )
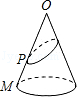
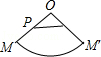
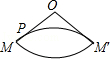
A. B. ![]() C. D.
C. D.
2.在函数y=![]() 的图象上有三个点的坐标为(1,y1),(
的图象上有三个点的坐标为(1,y1),(![]() ,y2),(-3,y3),函数值y1,y2,y3的大小关系为( )
,y2),(-3,y3),函数值y1,y2,y3的大小关系为( )
A. y1<y2<y3 B. y3<y2<y1 C. y2<y1<y3 D. y3<y1<y2
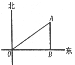
3.如图,小颖家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的400米处,那么水塔所在的位置到公路的距离AB是( )
A. 200米 B. 200![]() 米
米
C. ![]()
![]() 米 D. 400
米 D. 400![]() 米
米
4.抛物线y=a(x﹣4)2﹣3与x轴一个交点的坐标为(2,0),则与x轴另一个交点的坐标是( )
A.(0,0) B.(1,0) C.(4,0) D.(6,0)
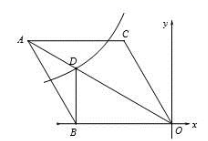
5.如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3![]() ),反比例函数
),反比例函数![]() 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
A. 6![]() B. -6
B. -6![]() C. 12
C. 12![]() D. -12
D. -12![]()
6.在△ABC中,∠C=90°,![]() ,则cosB的值是( )
,则cosB的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
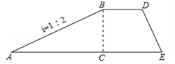
7.如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1:2,则斜坡AB的长为( )
A.4![]() 米 B.6
米 B.6![]() 米 C. 12
米 C. 12![]() 米 D. 24米
米 D. 24米
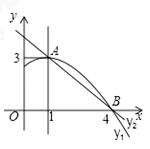
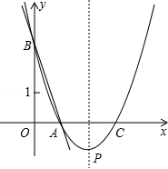
8.如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),![]() 与x轴的一个交
与x轴的一个交![]() 点为B,直线y2=mx+n(m≠0)经过A、B两点,下列结论: ①当x<1时,有y1<y2;②a+b+c=m+n;③b2﹣4ac=﹣12a;④若m﹣n=﹣5,则B点坐标为(4,0)
点为B,直线y2=mx+n(m≠0)经过A、B两点,下列结论: ①当x<1时,有y1<y2;②a+b+c=m+n;③b2﹣4ac=﹣12a;④若m﹣n=﹣5,则B点坐标为(4,0)
其中正确的是( )
A. ① B. ①② C. ①②③ D. ①②③④
9.一块直角三角板ABC按如图放置,顶点A的坐标为(0,1),直角顶点C的坐标为(﹣3,0),∠B=30°,则点B的坐标为( )
A.(﹣3﹣![]() ,3)
,3)
B.(﹣3﹣![]() ,3
,3![]() )
)
C.(﹣![]() ,3)
,3)
D.(﹣![]() ,3
,3![]() )
)

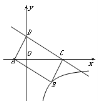
10.如图,直线![]() 与x 轴交于C,与y轴交于D, 以CD为边作矩形CDAB,点A在x轴上,双曲线y=
与x 轴交于C,与y轴交于D, 以CD为边作矩形CDAB,点A在x轴上,双曲线y=![]() (k<0)经过点B,则k的值为( )
(k<0)经过点B,则k的值为( )
A.1 B.3 C.4 D. -6
11.已知0≤x≤![]() ,则函数y=x2+x+1( )
,则函数y=x2+x+1( )
(A)有最小值![]() ,但无最大值
,但无最大值
(B)有最小值![]()
![]() ,有最大值1
,有最大值1
(C)有最小值1,有最大值![]()
(D)无最小值,也无最大值.
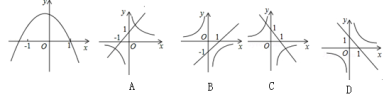
12.已知函数y=-(x-m)(x-n)(其中m<n)的图象如图所示,![]() 则一次函数y=mx+n与反比例函数y=
则一次函数y=mx+n与反比例函数y=![]() 的图象可能是( )
的图象可能是( )
13.
13.如图所示,点![]() P(3a,a)是反比例函数y=
P(3a,a)是反比例函数y=![]() (k>0
(k>0![]() )与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
A.y=![]() B.y=
B.y=![]() C.y=
C.y=![]() D.y=
D.y=![]()
14.在Rt△ABC中,∠C=90°,AB=5,BC=3,以AC所在的直线为轴旋转一周,所得圆锥的表面积为( )
A. ![]() B.
B.![]() C.
C.![]() D
D![]() .
.![]()
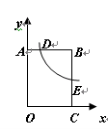
15.如图,双曲线![]() 经过矩形OABC的边BC的中点E,交AB于点D.若梯形ODBC的面积为5,则双曲线的解析式为()
经过矩形OABC的边BC的中点E,交AB于点D.若梯形ODBC的面积为5,则双曲线的解析式为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
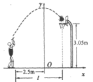
16.如图,小明在某次投篮中,球的运动路线是抛物线![]() 的一部分,若命中篮圈中心,则他与篮球架的距离l是( ).
的一部分,若命中篮圈中心,则他与篮球架的距离l是( ).
A.3.5m B.4m C.4.5m D.4.6m
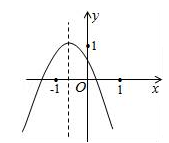
![]() 17.如图所示的二次函数y=ax2+bx+c的图象中,某同学观察得出了下面四条信息:
17.如图所示的二次函数y=ax2+bx+c的图象中,某同学观察得出了下面四条信息:
(1)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的有( )
A.2个![]() B.3个 C.4个 D.1个
B.3个 C.4个 D.1个
18.如图,正方形OABC,ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B,E在函数![]() 的图象上,则点E的横坐标是( )
的图象上,则点E的横坐标是( )
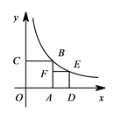
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
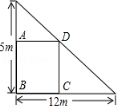
19.如图所示,在一个直角三角形的内部作一个长方形ABCD,其中AB和BC分别在两直角边上,设AB=![]() xm,长方形的面积为ym2,要使长方形的面积最大,其边长x应为( )
xm,长方形的面积为ym2,要使长方形的面积最大,其边长x应为( )
 A.
A.![]() m B.6m C.25m D.
m B.6m C.25m D.![]() m
m
20.如图,菱形OABC在直角坐标系中,点A的坐标为(5,0),对角线OB=![]() ,反比
,反比
例函数![]() (k≠0,x>0)经过点C.则k的值等于( )
(k≠0,x>0)经过点C.则k的值等于( )

A.12 B.8 C.15 D.9
二.填空题
21.已知反比例函数y=![]() (k≠0)的图象经过点(3,-1),则当1<y<3时,自变量x的取值范围是__________.
(k≠0)的图象经过点(3,-1),则当1<y<3时,自变量x的取值范围是__________.
22.如图,半径为5的⊙P与x轴交于点M(0,-4),N(0,-10). 函数y=![]() (x<0)的图
(x<0)的图
象过点P,则下列说法正确的有 .(填序号)
①⊙P与x轴相离; ②△PMN的面积为14;
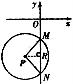
③⊙P的坐标为(-4,-7); ④k的值为28.
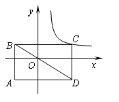
23.如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数![]() 的图象上.若点A的坐标为(-2,-2),则k的值为 。
的图象上.若点A的坐标为(-2,-2),则k的值为 。
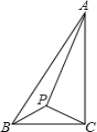
24.如图所示,P为△ABC内一点,∠BAC=30°,∠ACB=90°,∠BPC=12![]() 0°.若BP=
0°.若BP=![]() ,则△PAB的面积为 .
,则△PAB的面积为 .
三、解答题
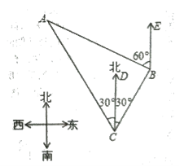
25.如图,我国渔政船在钓鱼岛海![]() 域C处测得钓鱼岛A在渔政船的北偏西30。的方向上,随后渔
域C处测得钓鱼岛A在渔政船的北偏西30。的方向上,随后渔![]() 政船以80海里/小时的速度向北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在渔政船的北偏西60°的方向上,求此时渔政船距钓鱼岛A的距离姓B.(结果保留小数点后一位,其中
政船以80海里/小时的速度向北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在渔政船的北偏西60°的方向上,求此时渔政船距钓鱼岛A的距离姓B.(结果保留小数点后一位,其中![]() 1.732)
1.732)
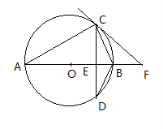
26.如图,⊙O的直径AB垂直弦CD于点E,点F在AB的延长线上,且∠BCF=∠A.
(1)求证:直线CF是⊙O的切线;
(2)若⊙O的半径为5,DB=4.求sinD的值.
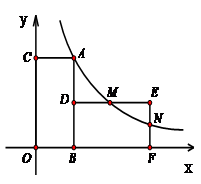
27.如图,面![]() 积为8的矩形
积为8的矩形![]() 的边
的边![]() 分别在
分别在![]() 轴,
轴,![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在反比例函数
在反比例函数![]() 的图象上,且
的图象上,且![]() .
.
(1)求反比例函数![]() 的解析式
的解析式
(2)将矩形![]() 以点
以点![]() 为旋转中心,顺时针旋转90°后得到矩形
为旋转中心,顺时针旋转90°后得到矩形![]() ,反比例函数图象交
,反比例函数图象交![]() 于
于![]() 点,
点,![]() 交
交![]() 于
于![]() 点.求
点.求![]() 的坐标.
的坐标.
(3)△MBN的面积
28.某水果超市以8元/千克的单价购进1000千克的苹果,为提高利润和便于销售,将苹果按大小分两种规格出售,计划大、小号苹果都为500千克,大号苹果单价定为16元/千克,小号苹果单价定为10元/千克,若大号苹果比计划每增加1千克,则大苹果单价减少0.03元,小号苹果比计划每减少1千克,则小苹果单价增加0.02元.设大号苹果比计划增加x千克.
(1)大号苹果的单价为 元/千克;小号苹果的单价为 元/千克;(用含x 的代数式表示)
(2)若水果超市售完购进的1000千克苹果,请解决以下问题:
①当x为何值时,所获利润最大?
②若所获利润为3385元,求x的值.
29.如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线![]() 经过点A、B,并与x轴交于另一点C,其顶点为P.
经过点A、B,并与x轴交于另一点C,其顶点为P.
(1)求![]() ,
,![]() 的值;
的值;
(2)抛物线的对称轴上有一点Q,使△ABQ是以AB为底边的等腰三角形,求Q点的坐标;
(3)在抛物线及其对称轴上分别取点M、N,使以A,C,M,N为顶点的四边形为正方形,求此正方形的边长.