请选择
返回
三角函数的降幂公式是:cos²α=(1+cos2α)/2;sin²α=(1-cos2α)/2;tan²α=(1-cos2α)/(1+cos2α)。降幂公式推导过程:运用二倍角公式就是升幂,将公式cos2α变形后可得到降幂公式:cos2α=cos²α-sin²α=2cos²α-1=1-2sin²α,降幂公式,就是降低指数幂由2次变为1次的公式,可以减轻二次方的麻烦。

三角函数降幂公式
三角函数的降幂公式是:cos²α=(1+cos2α)/2
sin²α=(1-cos2α)/2
tan²α=(1-cos2α)/(1+cos2α)
降幂公式推导过程:
运用二倍角公式就是升幂,将公式cos2α变形后可得到降幂公式:
cos2α=cos²α-sin²α=2cos²α-1=1-2sin²α
∴cos²α=(1+cos2α)/2
sin²α=(1-cos2α)/2
降幂公式,就是降低指数幂由2次变为1次的公式,可以减轻二次方的麻烦。
同角的正弦值、余弦值、正切值间的关系式
1、商数关系:tanA=sinA/cosA;tanB=sinB/cosB.
2、平方关系:同一个锐角的‘正弦的平方’与‘余弦的平方’的和为1,即
(sinA)^2+(cosA)^2=1;(sinB)^2+(cosB)^2=1.
3、倒数关系:tanA·cotA=1;tanB·cotB=1.
【注】“cotA”称为为∠A的余切,它等于∠A的邻边比上∠A的对边。“cotB”称为为∠B的余切,它等于∠B的邻边比上∠B的对边。
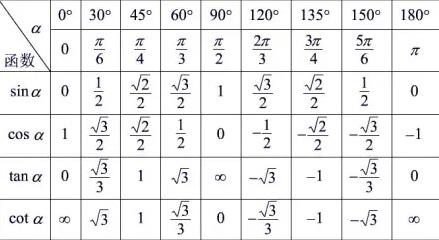
三角函数值对照表