请选择
2018年河南中考数学第三次模拟联考试题【精编免费版】
为了方便您的阅读请点击全屏查看
(考试时间:100分钟 试卷满分:120分)
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
5.考试范围:中考全部内容。
第Ⅰ卷
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)
1.7的算术平方根是
A.49 B.![]() C.-
C.-![]() D.±
D.±![]()
2.移动支付被称为中国新四大发明之一,据统计我国目前每分钟移动支付金额达3.79亿元,将数据3.79亿用科学记数法表示为
A.3.79×108 B.37.9×107 C.3.79×106 D.379×106
3.如图是五个棱长为“1”的立方块组成的一个几何体,不是三视图之一的是
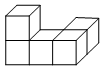
A.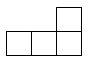 B.
B.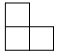 C.
C.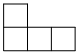 D.
D.
4.下列运算正确的是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.如图,BC⊥AE于点C,CD∥AB,∠B=50°,则∠1等于
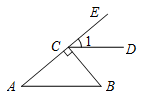
A.40° B.45° C.50° D.55°
6.若关于x的一元二次方程(k-1)x2+2x-2=0有两个不相等的实数根,则k的取值范围是
A.k>![]() B.k≥
B.k≥![]() C.k>
C.k>![]() 且k≠1 D.k≥
且k≠1 D.k≥![]() 且k≠1
且k≠1
7.如图,在![]() ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F,再分别以点E、F为圆心,大于
ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F,再分别以点E、F为圆心,大于![]() EF的长为半径画弧,两弧交于点G,作射线AG交CD于点H,则下列结论中不能由条件推理得出的是
EF的长为半径画弧,两弧交于点G,作射线AG交CD于点H,则下列结论中不能由条件推理得出的是
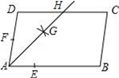
A.DH=BC B.CH=DH C.AG平分∠DAB D.AD=DH
8.在学校开展的“争做最优秀中学生”的一次演讲比赛中,编号1,2,3,4,5的五位同学最后成绩如表所示,那么这五位同学演讲成绩的众数与中位数依次是
参赛者编号 | 1 | 2 | 3 | 4 | 5 |
成绩/分 | 96 | 88 | 86 | 93 | 86 |
A.96,88 B.86,88 C.88,86 D.86,86
9.如图,扇形AOB中,OA=2,C为弧AB上的一点,连接AC,BC,如果四边形AOBC为菱形,则图中阴影部分的面积为

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知等边△ABC,顶点B(0,0),C(2,0),规定把△ABC先沿x轴绕着点C顺时针旋转,使点A落在x轴上,称为一次变换,再沿x轴绕着点A顺时针旋转,使点B落在x轴上,称为二次变换……,经过连续2017次变换后,顶点A的坐标是
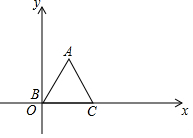
A.(4033,![]() ) B.(4033,0) C.(4036,
) B.(4033,0) C.(4036,![]() ) D.(4036,0)
) D.(4036,0)
第Ⅱ卷
二、填空题(本大题共5小题,每小题3分,共15分)
11.计算![]() -1-
-1-![]() =__________.
=__________.
12.不等式组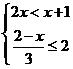 的最大整数解为__________.
的最大整数解为__________.
13.若二次函数![]() 的图象经过(2,0),且其对称轴为直线x=-1,则当函数值y>0成立时,x的取值范围是__________.
的图象经过(2,0),且其对称轴为直线x=-1,则当函数值y>0成立时,x的取值范围是__________.
14.质地均匀的正四面体骰子的四个面上分别写有数字:2,3,4,5.投掷这个正四面体两次,则第一次底面上的数字能够整除第二次底面上的数字的概率是__________.
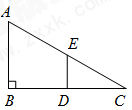
15.如图,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE.将△EDC绕点C按顺时针方向旋转,当△EDC旋转到A,D,E三点共线时,线段BD的长为__________.
三、解答题(本大题共8小题,共75分.解答应写出文字说明、证明过程或演算步骤)
16.(本小题满分8分)先化简![]() ,再从
,再从![]() 有意义的范围内选取一个整数作为a的值代入求值.
有意义的范围内选取一个整数作为a的值代入求值.
17.(本小题满分9分)某中学为了响应国家发展足球的战略方针,激发学生对足球的兴趣,特举办全员参与的“足球比赛”,赛后,全校随机抽查部分学生,其成绩(百分制)整理分成5组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:
成绩频数分布表
组别 | 成绩(分) | 频数 |
A | 50≤x<60 | 6 |
B | 60≤x<70 | m |
C | 70≤x<80 | 20 |
D | 80≤x<90 | 36 |
E | 90≤x<100 | n |
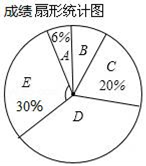
(1)频数分布表中的m=__________,n=__________;
(2)样本中位数所在成绩的级别是__________,扇形统计图中,E组所对应的扇形圆心角的度数是__________;
(3)若该校共有2000名学生,请你估计体育综合测试成绩不少于80分的大约有多少人?
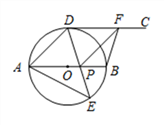
18.(本小题满分9分)如图,AB为⊙O的直径,点D,E是位于AB两侧的半圆AB上的动点,射线DC切⊙O于点D.连接DE,AE,DE与AB交于点P,F是射线DC上一动点,连接FP,FB,且∠AED=45°.
(1)求证:CD∥AB;
(2)填空:
①若DF=AP,当∠DAE=__________时,四边形ADFP是菱形;
②若BF⊥DF,当∠DAE=__________时,四边形BFDP是正方形.
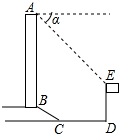
19.(本小题满分9分)如图,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1∶![]() ,求大楼AB的高度是多少?(结果保留根号)
,求大楼AB的高度是多少?(结果保留根号)
20.(本小题满分9分)某商店欲购进一批跳绳,若同时购进A种跳绳10根和B种跳绳7根,则共需395元,若同时购进A种跳绳5根和B种跳绳3根,共需185元.
(1)求A、B两种跳绳的单价各是多少?
(2)若该商店准备同时购进这两种跳绳共100根,且A种跳绳的数量不少于跳绳总数量的![]() .若每根A种跳绳的售价为26元,每根B种跳绳的售价为30元,问:该商店应如何进货才可获取最大利润,并求出最大利润.
.若每根A种跳绳的售价为26元,每根B种跳绳的售价为30元,问:该商店应如何进货才可获取最大利润,并求出最大利润.
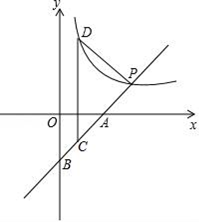
21.(本小题满分10分)如图,直线AB交x轴于点A(4,0),交y轴于点B,交反比例函数y=![]() (k≠0)于点P(第一象限),若点P的纵坐标为2,且tan∠BAO=1.
(k≠0)于点P(第一象限),若点P的纵坐标为2,且tan∠BAO=1.
(1)求出反比例函数y=![]() (k≠0)的解析式;
(k≠0)的解析式;
(2)过线段AB上一点C作x轴的垂线,交反比例函数y=![]() (k≠0)于点D,连接PD,当△CDP为等腰三角形时,求点C的坐标.
(k≠0)于点D,连接PD,当△CDP为等腰三角形时,求点C的坐标.
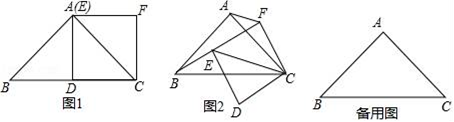
22.(本小题满分10分)(1)【问题发现】
如图1,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为__________.
(2)【拓展研究】
在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;
(3)【问题发现】
当正方形CDEF旋转到B,E,F三点共线时,直接写出线段AF的长.
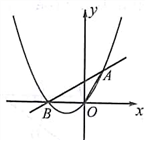
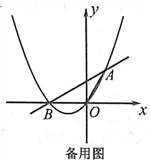
23.(本小题满分11分)如图,抛物线y=ax2+bx(a≠0)的图象过原点O和点A(1,![]() ),且与x轴交于点B,△AOB的面积为
),且与x轴交于点B,△AOB的面积为![]() .
.
(1)求抛物线的解析式;
(2)若抛物线的对称轴上存在一点M,使△AOM的周长最小,求M点的坐标;
(3)点F是x轴上一动点,过F作x轴的垂线,交直线AB于点E,交抛物线于点P,且PE=![]() ,直接写出点E的坐标(写出符合条件的两个点即可).
,直接写出点E的坐标(写出符合条件的两个点即可).