请选择
![]() 2018年天津中考数学冲刺试卷【精选word版 可下载】
2018年天津中考数学冲刺试卷【精选word版 可下载】
由于格式问题,部分试题会存在乱码的现象,请考生点击全屏查看!
一、选择题(每小题3分,共36分)
1.计算![]() 的结果等于
的结果等于
A.-2 B.-4 C.2 D.4
2.sin60°的值等于
3.下列图形中,可以看作是中心对称图形的是




A B C D
4.把503000000用科学记数法表示为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.如图,沿箭头所指的方向看一个正三棱柱,它的三视图是

A B C D
6.估计![]() 的值在
的值在
A.2和3之间 B.3和4之间 C.4和5之间 D.5和6之间
7.计算![]() 的结果为
的结果为
A.1 B.0 C.![]() D.-1
D.-1
8.如图,数轴上点 A、B 表示的数分别是![]() ,则下列结论中正确的是
,则下列结论中正确的是
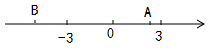
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
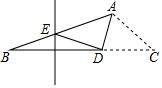
9.如图,在△ABC 中,∠BAC=120°,点 D 是 BC 上一点,BD 的重直平分钱交 AB 于点 E,将△ACD 沿 AD 折叠,点 C 恰好与点 E 重合,则∠B 等于
A.18° B.20° C.25° D.28°
10.若函数![]() 的图象与双曲线
的图象与双曲线![]() 相交,则当
相交,则当![]() 时,该交点位于
时,该交点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.如图,正方形 A8CD 中,E 为 AB 的中点,FE⊥AB,AF=2AE,FC 交 BD 于点 O,则∠DOC 的度数为
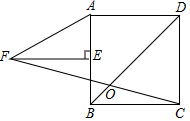
第9题 第11题
A.60° B.67.5° C.75° D.54°
12.已知抛物线![]() 经过点(-1,0),且满足
经过点(-1,0),且满足![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() ;③
;③![]() .其中,正确结论的个数是
.其中,正确结论的个数是
A.0 B.1 C.2 C.3
二、如空题(每小题3分,共18分)
13.计算![]() 的结果等于__________.
的结果等于__________.
14.计算![]() 的结果等于___________.
的结果等于___________.
15.甲、乙两袋均有红、黄色球各一个,分别从两袋中任意取出一球,那么所取出的两球是同色球的概率是______________.
16.已知一次函数的图象经过点(-2,2),但不经过第三象限,并且当![]() 时,
时,![]() 随
随![]() 的增大而减小,则符合条件的函数解析式可以是____________(写出一个即可).
的增大而减小,则符合条件的函数解析式可以是____________(写出一个即可).
17.如图,在正方形 ABCD 中,有面积为 4 的正方形 EFGH 和面积为 2 的正方形 PQMN,点 E、F、P、Q 分别在边 AB、BC、CD、AD 上,点 M、N 在边 HG 上,且组成的图形为轴对称图形,则正方形 ABCD 的面积为___________.
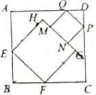
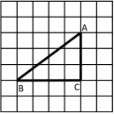
第17题 第18题
18.如图,将△ABC 放在每个小正方形的边长为 1 的网格中,点 A、点 B、点 C 均落在格点上。
(Ⅰ)线段 AB 的长度=_________.
(Ⅱ)请在如图所示的网格中,用无刻度的直尺,在∠ABC 的平分线上找一点 P,在 BC 上找一点 Q,使 CP+PQ的值最小,并简要说明点 P,Q 的位置是如何找到的___(不要求证明).
三、解答题(本大题共 7小题,共 6 分。解答应写出文字说明、演算步骤成推理时。
19.(本小题 8分)解不等式![]()
请结合题意填空,完成本题的解答:
(Ⅰ)解不等式(1),得________________.
(Ⅱ)解不等式(2),得________________.
(Ⅲ)把不等式(1)和(2)的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为____________.
20.(本小题8分)某地区在一次九年级数学检测中,有一道满分 8 分的解答题,按评分标准,所有学生的得分只有四种:0 分、3分、5 分、8 分,老师为了了解学生的得分情况,从全区 500 名考生的试卷中随机抽取一部分,通过分析与整理,绘制出如下两幅不完整的统计图①和图②。请根据相关信息,解答下列问题:
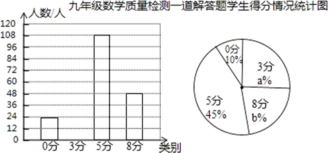
(Ⅰ)图①中a的值为_________;b 的值为____________.
(Ⅱ)求此样本数据的平均数、众数和中位数;
(Ⅲ)请估计该地区此题得满分(即 8分)的学生人数.
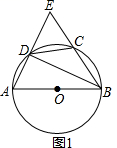
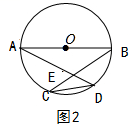
21.(本小题10分)已知 AB 是⊙O 的直径,AB=2,点 C,点 D 在⊙O 上,CD=1,直线 AD,BC 交于点 E.
(Ⅰ)如图1,若点 E 在⊙O 外,求∠AEB 的度数。
(Ⅱ)如图2,若点 E 在⊙O 内,求∠AEB 的的度数。
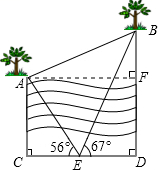
22.(本小题10分)如图,为求出河对岸两棵树 A、B 间的距离,小坤在河岸上选取一点 C,然后沿重直于 AC 的直线前进了 12m到达 D 点,测得∠CD8=90°,取 CD 的中点 E,测得∠AEC=56°,∠BED=67°,求河对岸两树间的距离。
(参考数据:sins56°≈![]() ,tan56°≈
,tan56°≈![]() ,sin67°≈
,sin67°≈![]() ,tan67°≈
,tan67°≈![]() )
)
23.(本小题10分)开发区某工厂生产的产品每件出厂价为 50 元,成本价为 25 元,在生产过程中,平均每生产一件产品有 0.5m![]() 污水排出,为了绿色环保达到排污标准,工厂投计两种处理污水的方案。
污水排出,为了绿色环保达到排污标准,工厂投计两种处理污水的方案。
方案一:工厂污水先净化处理后再排出,每处理 1m![]() 污水的费用为 2 元,并且每月排污设备损耗为 30000 元。
污水的费用为 2 元,并且每月排污设备损耗为 30000 元。
方案二:工厂将污水排到污水厂统一处理,每处理 1m![]() 污水的费用为 14 元。
污水的费用为 14 元。
设工厂每月生产![]() 件产品,每月利润为
件产品,每月利润为![]() 元(成本价不含排污费用)。
元(成本价不含排污费用)。
(Ⅰ)填写下表,并分别写出依据方案一和方落二处理污水时时![]() 与
与![]() 的关系式:
的关系式:
每月生产产品数(件) | 3000 | 7000 | 10000 |
|
方案一处理污水费用(元) | 33000 |
|
|
|
方案二处理污水费用(元) |
| 49000 |
|
|
方
(Ⅱ)如果你是该工厂的负责人,如何选择污水处理方案可使工厂利润最大?
24.(本小题10分)将平行四边形 OABC 放在平面直角坐标系中,O 为原点,点 C(-6,0),点 A 在第一象限,OA=2,∠A=60°.
(Ⅰ)如图①,求点 A 的坐标;
(Ⅱ)如图②,将平行四边形 OABC 绕点 O 逆时针旋转得到平行四边形![]() ,当点 A 的对应点
,当点 A 的对应点 ![]() 落在 y 轴正半轴上时,求旋转角及点 B 的对应点
落在 y 轴正半轴上时,求旋转角及点 B 的对应点![]() 的坐标
的坐标
(Ⅲ)将平行四边形 OABC 绕点 A 旋转得到平行四边形 DAEF,当点 B 的对应点 E 落在直线 OA 上时,求直线EF 的表达式(直接写出结果即可)。
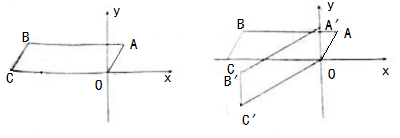
图① 图②
25.(本小题10分)在平面直角坐标系中,O 为原点,抛物线![]() 的顶点为 A,点 A 与点 O 关于点 B 对称。
的顶点为 A,点 A 与点 O 关于点 B 对称。
(Ⅰ)求点 A、点 B 的坐标:
(Ⅱ)过点 B 的直线![]() 与
与![]() 轴交于点 C,过点 C 作直线
轴交于点 C,过点 C 作直线![]() 垂直于
垂直于![]() 轴,P 是直线
轴,P 是直线![]() 上一点,且PB=PC,求线段 PB 的长(用含
上一点,且PB=PC,求线段 PB 的长(用含![]() 的式子表示),并判断点 P 是否在抛物线
的式子表示),并判断点 P 是否在抛物线![]() 上,请说明理由;
上,请说明理由;
(Ⅲ)将抛物线![]() ,沿
,沿![]() 轴翻折后,再向右平移,得抛物线
轴翻折后,再向右平移,得抛物线![]() ,当
,当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的最小值,
的最小值,