请选择
![]()
2018年廊坊中考数学冲刺试卷【精选word版 含答案】
由于格式问题,部分试题会存在乱码的现象,请考生点击全屏查看!
一、选择题(共16小题,1-10小题各3分,11-16小题各2分)
![]() 1.(3分)比﹣1小2017的数是( )
1.(3分)比﹣1小2017的数是( )
A.﹣2016 B.2016 C.2018 D.﹣2018
2.(3分)如图,已知在△ABC中,AD是高,若∠DAC=50°,则∠C的度数为( )

A.60° B.50° C.40° D.30°
3.(3分)中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4 400 000 000人,这个数用科学记数法表示为( )
A.4![]() 4×108 B.4.4×109 C.4.4×108 D.4.4×1010
4×108 B.4.4×109 C.4.4×108 D.4.4×1010
4.(3分)下列图形中,是中心对称图形但不是轴对称图形的是( )
A.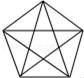 B.
B.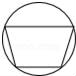 C.
C.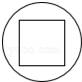 D.
D.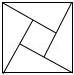
5.(3分)已知![]() +(b+2)2=0,则(a+b)2017的值为
+(b+2)2=0,则(a+b)2017的值为![]() ( )
( )
A.0 B.2016 C.﹣1 D.1
6.(3分)如图,在▱ABCD中,AD=7,点E、F分别是BD、CD的中点,则EF等于( )

A.2.5 B.3 C.4 D.3.5
7.(3分)已知实数a>0,则下列事件中是随机事件的是( )
A.a+3>0 B.a﹣3<0 C.3a>0 D.a3>0
8.(3分)若点A(1,2),B(﹣2,﹣3)在直线y=kx+b上,则函数y=![]() 的图象在( )
的图象在( )
A.第一、三象限 B.第一、二象限 C.第二、四象限 D.第二、三象限
9.(3分)如图,将边长相等的正方形、正五边形和正六边形摆放在平面上,则∠1为( )
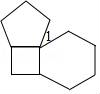
A.32° B.36° C.40° D.42°
10.(3分)关于x的一元二次方程x2﹣x+k=0有两个实数根,则k的取值范围是( )
A.k![]() B.k≥﹣
B.k≥﹣![]() C.k≤
C.k≤![]() D.k≤﹣
D.k≤﹣![]()
11.(2分)如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数是( )
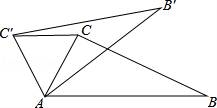
A.70° B.35° C.40° D.50°
12.(2分)当ab<0时,y=ax2与y=ax+b的图象大致是( )
A.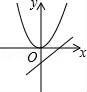 B.
B.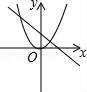 C.
C. D.
D.![]()

13.(2分)如图,一只蚂蚁沿边长为a的正方体表面从点A爬到点B,则它走过的路程最短为( )
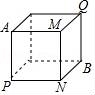
A.![]() a B.(1+
a B.(1+![]() )a C.3a D.
)a C.3a D.![]() a
a
14.(2分)为了举行班级晚会,小明准备去商店购买20个乒乓球做道具,并买一些乒乓球拍做奖品.已知乒乓球每个1.5元,球拍每个22元.如果购买金额不超过200元,购买的球拍为x个,那么x的最大值是( )
A.7 B.8 C.9 D.10
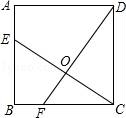
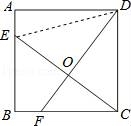
15.(2分)如图,正方形ABCD的边长为4,点E、F分别在AB、BC上,且AE=BF=1,CE、DF交于点O,下列结论:①∠DOC=90°,②OC=OE,③CE=DF,④tan∠OCD=![]() ,⑤S△DOC=S四边形EOFB中,正确的有( )
,⑤S△DOC=S四边形EOFB中,正确的有( )
A.1个 B.2个 C.3个 D.4个
16.(2分)某企业生产季节性产品,当产品无利润时,企业自动停产,经过调研,它一年中每月获得的利润y(万元)和月份n之间满足函数关系式y=﹣n2+12n﹣11,则企业停产的月份为( )![]()
A.1月和11月 B.1月、11月和12月
C.1月 D.1月至11月
二、填空题(每小题3分,共12分)
17.(3分)若|x|=2,则x的值是 .
18.(3分)如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为 .

19.(3分)在一个不透明的盒子中装有14个白球,若干个黄球,这些球除颜色外都相同,若从中随机摸出一个球是白球的概率是![]() ,则黄球的个数为 个.
,则黄球的个数为 个.
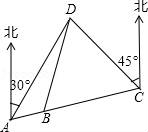
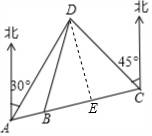
20.(3分)“奔跑吧,兄弟!”节目组预设计一个新游戏:“奔跑”路线A、B、C、D四地,如图A、B、C三地在同一直线上,D在A北偏东30°方向,在C北偏西45°方向,C在A北偏东75°方向,且BD=BC=40m,从A地到D地的距离是 m.
三、解答题(本大题共7小题,满分66分)
21.(8分)定义新运算:对于任意不为零的实数a、b,都有a★b=![]() ﹣
﹣![]() ,求方程x★(2﹣x)=
,求方程x★(2﹣x)=![]() 的解
的解![]() .
.
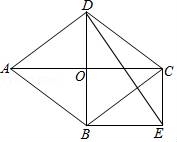
22.(8分)如图,在菱形ABCD中,对角线AC和BD交于点O,分别过点B、C作BE∥AC,CE∥BD,BE与CE交于点E.
(1)求证:四边形OBEC是矩形;
(2)当∠ABD=60°,AD=2![]() 时,求∠EDB的正切值.
时,求∠EDB的正切值.
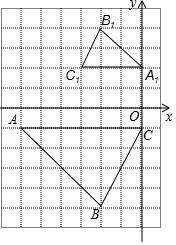
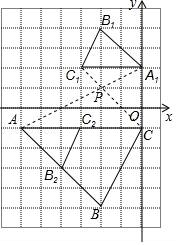
23.(9分)如图,△ABC与△A1B1C1是位似图形.
(1)在网格上建立平面直角坐标系,使得点A的坐标为(﹣6,﹣1),点C1的坐标为(﹣3,2),则点B的坐标为 ;
(2)以点A为位似中心,在网格图中作△AB2C2,使△AB2C2和△ABC位似,且位似比为1:2;
(3)在图上标出△ABC与△A1B1C1的位似中心P,并写出点P的坐标为 ,计算四边形ABCP的周长为 .
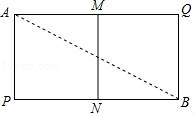
24.(9分)如图,直线y=kx+b过点A(5,0)和点C,反比例函数y=![]() (x<0)过点D,作BD∥x轴交y轴于点B(0,﹣3),且BD=OC,tan∠OAC=
(x<0)过点D,作BD∥x轴交y轴于点B(0,﹣3),且BD=OC,tan∠OAC=![]() .
.
(1)求反比例函数y=![]() (x<0)和直线y=kx+b的解析式;
(x<0)和直线y=kx+b的解析式;
(2)连接CD,判断线段AC与线段CD的关系,并说明理由.

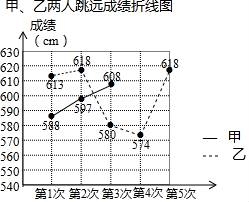
25.(10分)某班级选派甲、乙两位同学参加学校的跳远比赛,体育老师对他们的5次训练成绩进行了整理,并绘制了不完整的统计图,如图所示,请根据图中信息,解答下列问题:
甲、乙两人跳远成绩统计表:
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
甲成绩/厘米 | 588 | 597 | 608 | 610 | 597 |
乙成绩/厘米 | 613 | 618 | 580 | a | 618 |
根据以上信息,请解答下列问![]() 题:
题:
(1)a= ;
(2)请完成图中表示甲成绩变化情况的折线;
(3)通过计算,补充完整下面的统计分析表;
运动员 | 最好成绩 | 平均数 | 众数 | 方差 |
甲 |
|
| 597 | 41.2 |
乙 | 618 | 600.6 |
| 378.24 |
(4)请依据(3)中所统计的数据分析,甲、乙两位同学的训练成绩各有什么特点.
26.(11分)A、B两城相距900千米,一辆客车从A城开往B城,车速为每小时80千米,同时一辆出租车从B城开往A城,车速为每小时100千米,设客车出发时间为t(小时).
探究 若客车、出租车距A城的距离分别为y1、y2,写出y1、y2关于t的函数关系式及自变量取值范围,并计算当y1=240千米时y2的値.
发现 (1)设点C是A城与B城的中点,AC=![]() AB,通过计算说明:哪个车先到达C城?该车到达C后再经过多少小时,另一个车会到达C?
AB,通过计算说明:哪个车先到达C城?该车到达C后再经过多少小时,另一个车会到达C?
(2)若两车扣相距100千米时,求时间t.
决策 已知客车和出租车正好在A,B之间的服务站D处相遇,此时出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种选择返回B城的方案:
方案一:继续乘坐出租车到C城,加油后立刻返回B城,出租车加油时间忽略不计;
方案二:在D处换乘客车返回B城.
试通过计算,分析小王选择哪种方式能更快到达B城?
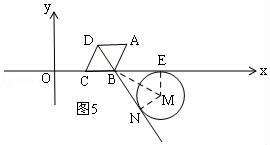
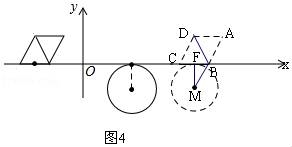
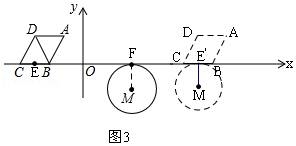
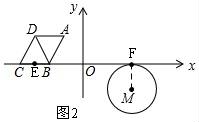
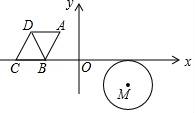
27.(11分)如图,⊙M与菱形ABCD在平面直角坐标系中,点M的坐标为(3,﹣1),点A的坐标为(﹣2,![]() ),点B的坐标为(﹣3,0),点C在x轴上,且点D在点A的左侧.
),点B的坐标为(﹣3,0),点C在x轴上,且点D在点A的左侧.
(1)求菱形ABCD的周长;
(2)若⊙M沿x轴向右以每秒2个单位长度的速度平移,同时菱形ABCD沿x轴向右以每秒3个单位长度的速度平移,设菱形移动的时间为t(秒),当⊙M与BC相切,且切点为BC的中点时,连接BD,求:
①t的值;
②∠MBD的度数;
(3)在(2)的条件下,当点M与BD所在的直线的距离为1时,求t的值.
2018年廊坊中考数学冲刺试卷参考答案与试题解析
一、选择题(共16小题,1-10小题各3分,11-16小题各2分)
1.
【解答】解:﹣1﹣2017=﹣1+(﹣![]() 2017)=﹣2018.
2017)=﹣2018.
故选:D.
2.
【解答】解:∵AD⊥BC,
∴∠ADC=90°.
∵∠DAC=50°,
∴∠C=90°﹣50°=40°.
故选:C.
3.
【解答】解:4 400 000 000=4.4×109,
故选:B.
4.
【解答】解:A、是轴对称图形,不是中心对称图形,故错误;
B、是轴对称图形,不是中心对称图形,故错误;
C、是轴对称图形,也是中心对称图形,故错误;
D、不是轴对称图形,是中心对称图形,故正确.
故选:D.
5.
【解答】解:由题意得,a﹣1=0,b+2=0,
解得,a=1,b=﹣2,
则(a+b)2017=﹣1,
故选:C.![]()
6.
【解答】解:∵四边形ABCD是平行四边形,
∴BC=AD=7,
∵点E、F分别是BD、CD的中点,
∴EF=![]() BC=
BC=![]() ×7=3.5.
×7=3.5.
故选:D.
7.
【解答】解:A、∵a>0,∴a+3>3>0是必然事件,不符合题意;
B、∵a>0,∴a+3可能大于零,可能小于零,可能等于零是随机事件,符合题意;
C、∵a>0,∴都乘以3,不等号的方向不变,3a>0是必然事件,不符合题意;
D、∵a>0,∴a3>0是必然事件,不符合题意.
故选:B.
8.
【解答】解:∵点A(1,2),B(﹣2,﹣3)在直线y=kx+b上,
∴![]() ,解得:
,解得:![]() ,
,
∴函数y=![]() 的图象在第一、三象限.
的图象在第一、三象限.
故选:A.
9.
【解答】解:正方形的内角为90°,
正五边形的内角为![]() =108°,
=108°,
正六边形的内角为![]() =120°,
=120°,
∠1=360°﹣90°﹣108°﹣120°=42°,
故选:D.
10.
【解答】解:根据题意得△=(﹣1)2﹣4k≥0,
解得k≤![]() .
.
故选:C.
11.
【解答】解:∵△ABC绕点A逆时针旋转到△AB′C′的位置,
∴AC′=AC,∠B′AB=∠C′AC,
∴∠AC′C=∠ACC′,
∵CC′∥AB,
∴∠ACC′=∠CAB=70°,
∴∠AC′C=∠ACC′=70°,
∴∠CAC′=180°﹣2×70°=40°,
∴∠B′AB=40°,
故选:C.
12.
【解答】解:根据题意,ab<0,
当a>0时,b<0,y=ax2与开口向上,过原点,y=ax+b过一、三、四象限;
此时,A选项符合,
当a<0时,b>0,y=ax2与开口向下,过原点,y=ax+b过一、二、四象限;
此时,没有选项符合.
故选:A.
13.
【解答】解:如图,则AB=![]() =
=![]() =
=![]() a.
a.
故选:D.
14.
【解答】解:设购买球拍x个,依题意得:
1.5×20+22x≤200,
解之得:x≤7![]() ,
,
∵x取整数,
∴x的最大值为7;
故选:A.
15.
【解答】解:∵正方形ABCD的边长为4,
∴BC=CD=4,∠B=∠DCF=90°,
∵AE=BF=1,
∴BE=CF=4﹣1=3,
在△EBC和△FCD中,
 ,
,
∴△EBC≌△FCD(SAS),
∴∠CFD=∠BEC,CE=DF,故③正确,
∴∠BCE+∠BEC=∠BCE+∠CFD=90°,
∴∠DOC=90°;故①正确;
连接DE,如图所示:
若OC=OE,
∵DF⊥EC,
∴CD=DE,
∵CD=AD<DE(矛盾),故②错误;
∵∠OCD+∠CDF=90°,∠CDF+∠DFC=90°,
∴∠OCD=∠DFC,
∴tan∠OCD=tan∠DFC=![]() =
=![]() ,故④正确;
,故④正确;
∵△EBC≌△FCD,
∴S△EBC=S△FCD,
∴S△EBC﹣S△FOC=S△FCD﹣S△FOC,
即S△ODC=S四边形BEOF.故⑤正确;
故正确的有:①③④⑤,
故选:D.
16.
【解答】解:由题意知,
利润y和月份n之间函数关系式为y=﹣n2+12n﹣11,
∴y=﹣(n﹣6)2+25,
当n=1时,y=0,
当n=11时,y=0,
当n=12时,y<0,
故停产的月份是1月、11月、12月.
故选:B.
二、填空题(每小题3分,共12分)
17.
【解答】解:∵|2|=2,|﹣2|=2,
∴x=±2.
故答案为:±2.
18.
【解答】解:∵∠A=50°,
∴∠BOC=2∠A=100°,
∵∠B=30°,∠BOC=∠B+∠BDC,
∴∠BDC=∠BOC﹣∠B=100°﹣30°=70°,![]()
∴∠ADC=180°﹣∠BDC=110°,
故答案为110°.
![]()
19.
【解答】解:设黄球的个数为x,根据题意得:
![]() =
=![]() ,
,
解得:x=28,
答:黄球的个数为28个;
故答案为:28.
20.
【解答】解:过点D作DE⊥BC于E,如图所示.
由题意可知:∠DAC=75°﹣30°=45°,∠BCD=180°﹣75°﹣45°=60°.
∵BC=BD=40m,
∴△BCD为等边三角形,
∴DE=![]() BD=20
BD=20![]() m.
m.
在Rt△ADE中,∠AED=90°,∠DAE=45°,
∴∠ADE=45°,
∴AE=DE=20![]() m,AD=
m,AD=![]() =20
=20![]() m.
m.
故答案为:20![]() .
.
三、解答题(本大题共7小题,满分66分)
21.
【解答】解:∵a★b=![]() ﹣
﹣![]() ,
,
∴x★(2﹣x)=![]() ﹣
﹣![]() =
=![]() ,
,
两边同时乘x(2﹣x),可得:2﹣x﹣x=﹣6,
解得x=4,
经检验,x=4是原分式方程的解,
∴原分式方程的解为:x=4.
22.
【解答】解:(1)∵BE∥AC,CE∥BD,
∴四边形OBEC为平行四边形.
∵ABCD为菱形,
∴AC⊥BD.
∴∠BOC=90°.
∴四边形OBEC是矩形.
(2)∵AD=AB,∠DAB=60°,
∴△ABD为等边三角形.
∴BD=AD=AB=2![]() .
.
∵ABCD为菱形,∠DAB=60°,
∴∠BAO=30°.
∴OC=OA=3.
∴BE=3
∴tan∠EDB=![]() =
=![]() =
=![]() .
.
23.
【解答】解:(1)如图所示:点B的坐标为:(﹣2,﹣5);
故答案为:(﹣2,﹣5);
(2)如图所示:△AB2C2,即为所求;
(3)如图所示:P点即为所求,P点坐标为:(﹣2,1),
四边形ABCP的周长为:![]() +
+![]() +
+![]() +
+![]() =4
=4![]() +2
+2![]() +2
+2![]() +2
+2![]() =6
=6![]() +4
+4![]() .
.
故答案为:6![]() +4
+4![]() .
.
24.
【解答】解:(1)∵A(5,0),
∴OA=5.
∵tan∠OAC=![]() .
.
∴![]() =
=![]() .
.
解得OC=2,
∴C(0,2),
∴BD=OC=2,
∵B(0,﹣3),BD∥x轴,
∴D(﹣2,﹣3),
∴m=﹣2×(﹣3)=6,
∴y=![]() ,
,
设直线AC关系式为y=kx+b,
∵过A(5,0),C(0,2),
∴![]() ,
,
解得![]() ,
,
∴y=﹣![]() +2;
+2;
(2)∵B(0,﹣3),C(0,2),
∴BC=5=OA,
∵x轴⊥y轴,∠AOC=∠COE=90°,BD∥x轴,
∴∠COE=∠DBC=90°,
∴∠AOC=∠DBC.
在△OAC和△BCD中
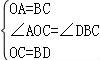
∴△OAC≌△BCD(SAS),
∴AC=CD,
∴∠OAC=∠BCD,
∴∠BCD+∠BCA=∠OAC+∠BCA=90°,
∴AC⊥CD.

25.
【解答】解:(1)由折线统计图可知,a=574;
(2)如图所示:

(3)甲的平均数:(588+597+608+610+597)÷5=600
填表如下:
运动员 | 最好成绩 | 平均数 | 众数 | 方差 |
甲 | 610 | 600 | 597 | 41.2 |
乙 | 618 | 600.6 | 618 | 378.24 |
(4)从最好成绩,平均数,众数来看,乙跳远的成绩优于甲的;
从方差来看,甲方差小说明甲成绩比乙的成绩稳定.
故答案为:574;610,600,618.
26.
【解答】解:探究:由已知得,y1=80t(0≤t≤![]() ),y2=900﹣100t(0≤t≤9),
),y2=900﹣100t(0≤t≤9),
当y1=240时,即80t=240,
∴t![]() =3,
=3,
∴y2=900﹣100×3=600;
发现:(1)∵AC=![]() AB=
AB=![]() 900=300km,
900=300km,
∴客车到达C点需要的时间:80t1=300,
解得:t1=3.75;
出租车到达C点需要的时间:900﹣100t2=300,
解得:t2=6>3.75,6﹣3.75=2.25,
∴客车先到达C,再过2.25小时出租车到达;
(2)两车相距100千米,分两种情况:
①y2![]() ﹣y1=100,即900﹣80t﹣100t=100,
﹣y1=100,即900﹣80t﹣100t=100,
解得:t=![]() ;
;
②y1﹣y2=100,即80t﹣(900﹣100t)=100,
解得:t=![]() .
.
综上可知:两车相距100千米时,时间t为![]() 或
或![]() 小时.
小时.
决策:两车相遇,即80t+100t=900,解得t=5,
此时AD=80×5=400(千米),BD=900﹣400=500(千米).
方案一:t1=(2CD+BD)÷100=7(小时);
方案二:t2=500÷80=6.25(小时).
∵t1>t2,
∴方案二更快.
27.
【解答】解:(1)如图1,过A作AE⊥BC于E,
∵点A的坐标为(﹣2,![]() ),点B的坐标为(﹣3,0),
),点B的坐标为(﹣3,0),
∴AE=![]() ,BE=3﹣2=1,
,BE=3﹣2=1,
∴AB=![]() =
=![]() =2,
=2,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=2,
∴菱形ABCD的周长=2×4=8;
(2)①如图2,⊙M与x轴的切点为F,BC的中点为E,
∵M(3,﹣1),
∴F(3,0),
∵BC=2,且E为BC的中点,
∴E(﹣4,0),
∴EF=7,
即EE'﹣FE'=EF,
∴3t﹣2t=7,
t=7,
②由(1)可知:BE=1,AE=![]() ,
,
∴tan∠EBA=![]() =
=![]() =
=![]() ,
,
∴∠EBA=60°,
如图4,∴∠FBA=120°,
∵四边形ABCD是菱形,
∴∠FBD=![]() ∠FBA=
∠FBA=![]() =60°,
=60°,
∵BC是⊙M的切线,
∴MF⊥BC,
∵F是BC的中点,
∴BF=MF=1,
∴△BFM是等腰直角三角形,
∴∠MBF=45°,
∴∠MBD=∠MBF+∠FBD=45°+60°=105°;
(3)连接BM,过M作MN⊥BD,垂足为N,作ME⊥BC于E,
第一种情况:如图5,
∵四边形ABCD是菱形,∠ABC=120°,
∴∠CBD=60°,
∴∠NBE=60°,
∵点M与BD所在的直线的距离为1,
∴MN=1,
∴BD为⊙M的切线,
∵BC是⊙M的切线,
∴∠MBE=30°,
∵ME=1,
∴EB=![]() ,
,
∴3t+![]() =2t+6,
=2t+6,
t=6﹣![]() ;
;
第二种情况:如图6,∵四边形ABCD是菱形,∠ABC=120°,![]()
∴∠DBC=60°,
∴∠NBE=120°,
∵点M与BD所在的直线的距离为1,
∴MN=1,
∴BD为⊙M的切线,
∵BC是⊙M的切线,
∴∠MBE=60°,
∵ME=MN=1,
∴Rt△BEM中,tan60°=![]() ,
,
EB=![]() =
=![]() ,
,
∴3t=2t+6+![]() ,
,
t=6+![]() ;
;
综上所述,当点M与BD所在的直线的距离为1时,t=6﹣![]() 或6+
或6+![]() .[:Z|xx|k.Com]
.[:Z|xx|k.Com]