请选择
四川省自贡市初2018届毕业生学业考试
![]() 数 学 试 卷
数 学 试 卷
本试题![]() 卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共6页,满分150分.答卷前,考生务必将自己的姓名,准考证号填写在答题卡上,并在规定位置粘贴考试用的条形码,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效,考试结束后,将试题卷和答题卡一并交回.
卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共6页,满分150分.答卷前,考生务必将自己的姓名,准考证号填写在答题卡上,并在规定位置粘贴考试用的条形码,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效,考试结束后,将试题卷和答题卡一并交回.
第![]() Ⅰ卷 选择题 (共48分)
Ⅰ卷 选择题 (共48分)
注意事项:必须使用2B铅笔将答案标号填涂在答题卡对应题目标号的位置上,如需改动用橡皮擦擦干净,再选涂答案标号.
一.选择题(共12个小题,每小题4分,共48分;在每题给出的四个选项中,只有一项是符合题目要求的)
1.计算![]() 的结果是 ( )
的结果是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.下列计算正确的是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.2017年我市用于资助贫困学生的助学金总额是445800000元,将445800000用科学记数法表示为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
- 在平面内,将一个直角三角板按如图所示摆放在一组平行线上;若
 ,则
,则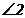 的度数是 ( )
的度数是 ( )
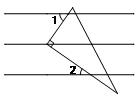
A.50° B.45° C.40° D.35°
5.下面几何体的主视图是 ( )
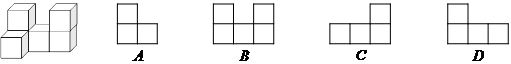
6.如图,在⊿![]() 中,点
中,点![]() 分别是
分别是![]() 的中点,若⊿
的中点,若⊿![]()
的面积为4,则是⊿![]() 的面积为 ( )
的面积为 ( )
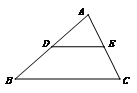
A. 8 B. 12 C. 14 D. 16
7.在一次数学测试后,随机抽取九年级(3)班5名学生的成绩(单位:分)如下:80、98、98、83、91,关于这组数据的说法错误的是 ![]() ( )
( )
A.众数是![]() B.平均数是
B.平均数是![]() C.中位数是
C.中位数是![]() D.方差是
D.方差是![]()
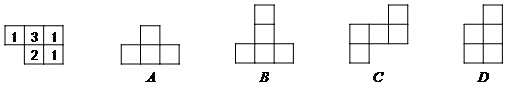 8.回顾初中阶段函数的学习过程,从函数解析式到函数图象
8.回顾初中阶段函数的学习过程,从函数解析式到函数图象![]() ,再利用函数图象研究函数的性质
,再利用函数图象研究函数的性质![]() ,这种研究方法主要体现的数学思想
,这种研究方法主要体现的数学思想![]() 是 ( )
是 ( )
A.数形结合 B.类比 C.演绎 D.公理化
9.如图,若⊿![]() 内接于半径为
内接于半径为![]() 的⊙
的⊙![]() ,且
,且![]() ,连接
,连接![]() ,则
,则
边![]() 的长为
的长为
 ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.从![]() 这四个数中任取两数,分别记为
这四个数中任取两数,分别记为![]() ,那么点
,那么点![]() 在函数
在函数![]() 图象的概率是 ( )
图象的概率是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知圆锥的侧面积是![]() ,若圆锥底面半径为
,若圆锥底面半径为![]() ,母线长为
,母线长为![]() ,则
,则![]() 关于
关于![]() 的函数图象大致是 ( )
的函数图象大致是 ( )
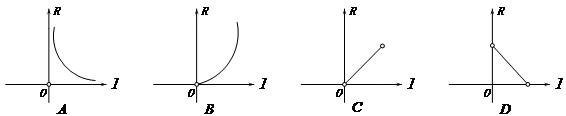
- 如图,在边长为
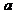 正方形
正方形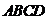 中,把边
中,把边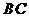 绕点
绕点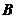 逆时针旋转60°,得到线段
逆时针旋转60°,得到线段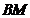 ,连接
,连接 并延长交
并延长交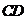 于
于 ,连接
,连接 ,则⊿
,则⊿ 的面积为 ( )
的面积为 ( ) 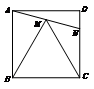
A.![]() B.
B.![]()
C. ![]() D.
D.![]()
第Ⅱ卷 非选择题 (共102分)
注意事项:必须使用0.5毫米黑色墨水铅签字笔在答题卡上题目所指示区域内作答,作图题
可先用铅笔绘出,确认后用0.5毫米黑色墨水铅签字笔描清楚,答在试题卷上无效.
二.填空题(共6个小题,每题4分,共24分)
13. 分解因式:![]() = .
= .
14.化简![]() 的结果是 .
的结果是 .
15.若函数![]() 的图象与
的图象与![]() 轴有且只有一个交点,则
轴有且只有一个交点,则![]() 的值为 .
的值为 .
16.六一儿童节,某幼儿园用100元钱给小朋友买了甲、乙两种不同的玩具共30个,单价分别为2元和4元,则该幼儿园购买了甲、乙两种玩具分别为 、 个.
17.观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2018个图形共有 个○.
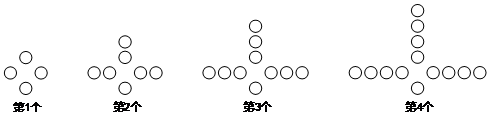
18.如图,在⊿![]() 中,
中,![]() ,将它沿
,将它沿![]() 翻折得到⊿
翻折得到⊿![]() ,则
,则
四边形![]() 的形状是 形,点
的形状是 形,点![]() 分别为线段
分别为线段![]() 的
的
任意点,则![]() 的最小值是
的最小值是
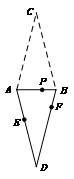 .
.
三、 解答题(共8个题,共78分)
19.(本题满分8分) 计算:![]() .
.
20..(本题满分8分)解不等式组: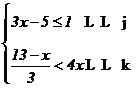 ,并在数轴上
,并在数轴上![]() 表示其解集.
表示其解集.
21.(本题满分8分) 某校研究学生的课余爱好情况吧,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成下面两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
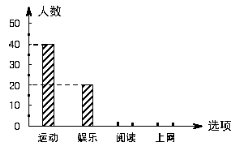

⑴.在这次调查中,一共调查了 名学生;
⑵.补全条形统计图;
⑶.若该校共有1500名,估计爱好运动的学生有 人;
⑷.在全校同学中随机选取一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生的概率是 .
22.(本题满分8分)如图,在⊿![]() 中,
中,![]() ;求
;求![]() 和
和![]() 的长.
的长.
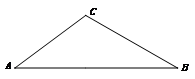
23.(本题满分10分)如图,在⊿![]() 中,
中,![]() .
.
⑴.作出经过点![]() ,圆心
,圆心![]() 在斜边
在斜边![]() 上且与边
上且与边![]() 相切于点
相切于点![]() 的⊙
的⊙![]() ;
;
(要求:用尺规作图,保留作图痕迹,不写作法和证明)
⑵.设⑴中所作的⊙![]() 与边
与边![]() 交于异于点
交于异于点![]() 的另外一点
的另外一点![]() ,若⊙
,若⊙![]() 的直径为5,
的直径为5,![]() ;求
;求![]() 的长.(如果用尺规作图画不出图形,可画出草图完成⑵问)
的长.(如果用尺规作图画不出图形,可画出草图完成⑵问)

24.(本题满分10分)阅读以下材料:
对数![]() 的创始人是苏格兰数学家纳皮尔(J.Nplcr,1550 – 1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evlcr,1707 – 1783年)才发现指数与对数之间的联系.
的创始人是苏格兰数学家纳皮尔(J.Nplcr,1550 – 1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evlcr,1707 – 1783年)才发现指数与对数之间的联系.
对数的定义:一般地,若![]() ,那么
,那么![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记作:
的对数,记作:![]() .比如指数式
.比如指数式![]() 可以转化为
可以转化为![]() ,对数式
,对数式![]() 可以转化为
可以转化为![]() .
.
我们根据对数的定义可得到对数的一个性质:
![]() ;理由如下:
;理由如下:
设![]() ,则
,则![]()
∴![]() ,由对数的定义得
,由对数的定义得![]()
又∵![]()
∴![]()
解决以下问题:
⑴.将指数![]() 转化为对数式 ;
转化为对数式 ;
⑵.证明![]()
⑶.拓展运用:计算![]() = .
= .
25.![]() (本题满分12分)如图,已知
(本题满分12分)如图,已知![]() ,在
,在![]() 的平分线
的平分线![]() 上有一点
上有一点![]() ,将一个120°角的顶点与点
,将一个120°角的顶点与点![]() 重合,它
重合,它![]() 的两条边分别与直线
的两条边分别与直线![]() 相交于点
相交于点![]() .
.
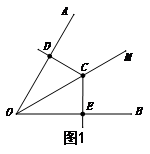
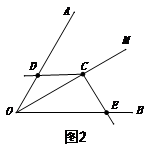

⑴.当![]() 绕点
绕点![]()
![]() 旋转到
旋转到![]() 与
与![]() 垂直时(如图1),请猜想
垂直时(如图1),请猜想![]() 与
与![]() 的数量关系,并说明
的数量关系,并说明![]() 理由;
理由;
⑵.当![]() 绕点
绕点![]() 旋转到
旋转到![]() 与
与![]() 不垂直时,到达图2的位置,⑴中的结论是否成立?并说明理由;
不垂直时,到达图2的位置,⑴中的结论是否成立?并说明理由;
⑶.当![]() 绕点
绕点![]() 旋转到
旋转到![]() 与
与![]() 的反向延长线相交时,上述结论是否成
的反向延长线相交时,上述结论是否成![]() 立?请在图3中画出图形,若成立,请给于证明;若不成立,线段
立?请在图3中画出图形,若成立,请给于证明;若不成立,线段![]() 与
与![]() 之间又有怎样的数量关系?请写出你的猜想,不需证明.
之间又有怎样的数量关系?请写出你的猜想,不需证明.
26.(本题满分14分)
如图,抛物线![]() 过
过![]() ,直线
,直线![]() 交抛物线于点
交抛物线于点![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 是线段
是线段![]() 上的动点.
上的动点.
⑴.求直线![]() 及抛物线的解析式;
及抛物线的解析式;
⑵.过点![]() 的直线垂直于
的直线垂直于![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,求线段
,求线段![]() 的长度
的长度![]() 与
与![]() 的关系式,
的关系式,![]() 为何值时,
为何值时,![]() 最长?
最长?
⑶.在平面内是否存在整点(横、纵坐标都为整数)![]() ,使得
,使得![]() 为顶点的四边形是平行四边形?若存在,直接写出点
为顶点的四边形是平行四边形?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.


![]()
![]()