请选择
![]() 河北省2018年中考数学试卷
河北省2018年中考数学试卷
卷Ⅰ(选择题,共42分)
一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列图形具有稳定性的是( )
A.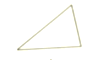 B.
B. C.
C. D.
D.
2.一个整数![]() 用科学记数法表示为
用科学记数法表示为![]() ,则原数中“0”的个数为( )
,则原数中“0”的个数为( )
A.4 B.6 C.7 D.10
3.图1中由“○”和“□”组成轴对称图形,该图形的对称轴是直线( )
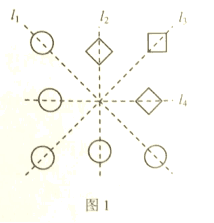
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.将![]() 变形正确的是( )
变形正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.图2中三视图对应的几何体是( )

A. B.
B. 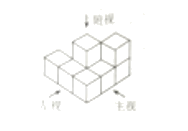
C.  D.
D.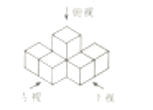
6.尺规作图要求:Ⅰ.过直线外一点作这条直线的垂线;Ⅱ.作线段的垂直平分线;Ⅲ.过直线上一点作这条直线的垂线;Ⅳ.作角的平分线.
图3是按上述要求排乱顺序的尺规作图:
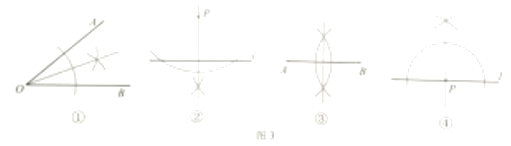
则正确的配对是( )
A.①-Ⅳ,②-Ⅱ,③-Ⅰ,④-Ⅲ B.①-Ⅳ,②-Ⅲ,③-Ⅱ,④-Ⅰ
C. ①-Ⅱ,②-Ⅳ,③-Ⅲ,④-Ⅰ D.①-Ⅳ,②-Ⅰ,③-Ⅱ,④-Ⅲ
7.有三种不同质量的物体,“![]() ”“
”“![]() ”“
”“![]() ”其中,同一种物体的质量都相等,现左右手中同样的盘子上都放着不同个数的物体,只有一组左右质量不相等,则该组是( )
”其中,同一种物体的质量都相等,现左右手中同样的盘子上都放着不同个数的物体,只有一组左右质量不相等,则该组是( )
A. B.
B.
C.  D.
D.
![]()
8.已知:如图4,点![]() 在线段
在线段![]() 外,且
外,且![]() .求证:点
.求证:点![]() 在线段
在线段![]() 的垂直平分线上.在证明该结论时,需添加辅助线,则作法不正确的是( )
的垂直平分线上.在证明该结论时,需添加辅助线,则作法不正确的是( )
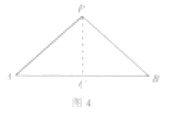
A.作![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]()
B.过点![]() 作
作![]() 于点
于点![]() 且
且![]()
C.取![]() 中点
中点![]() ,连接
,连接![]()
D.过点![]() 作
作![]() ,垂足为
,垂足为![]()
9.为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机抽取部分麦苗,获得苗高(单位:![]() )的平均数与方差为:
)的平均数与方差为:![]() ,
,![]() ;
;![]() ,
,![]() .则麦苗又高又整齐的是( )
.则麦苗又高又整齐的是( )
A.甲 B.乙 C.丙 D.丁
10.图5中的手机截屏内容是某同学完成的作业,他做对的题数是( )

A.2个 B.3个 C. 4个 D.5个
11.如图6,快艇从![]() 处向正北航行到
处向正北航行到![]() 处时,向左转
处时,向左转![]() 航行到
航行到![]() 处,再向右转
处,再向右转![]() 继续航行,此时的航行方向为( )
继续航行,此时的航行方向为( )
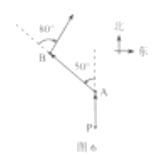
A.北偏东![]() B.北偏东
B.北偏东![]()
C.北偏西![]() D.北偏西
D.北偏西![]()
12.用一根长为![]() (单位:
(单位:![]() )的铁丝,首尾相接围成一个正方形.要将它按图7的方式向外等距扩1(单位:
)的铁丝,首尾相接围成一个正方形.要将它按图7的方式向外等距扩1(单位:![]() ), 得到新的正方形,则这根铁丝需增加( )
), 得到新的正方形,则这根铁丝需增加( )
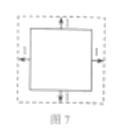
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13.若![]() ,则
,则![]() ( )
( )
A.-1 B.-2 C.0 D.![]()
14.老师设计了接力游戏,用合作的方式完成分式化简.规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简.过程如图8所示:
接力中,自己负责的一步出现错误的是( )

A.只有乙
B.甲和丁
C.乙和丙
D.乙和丁
15.如图9,点![]() 为
为![]() 的内心,
的内心,![]() ,
,![]() ,
,![]() ,将
,将![]() 平移使其顶点与
平移使其顶点与![]() 重合,则图中阴影部分的周长为( )
重合,则图中阴影部分的周长为( )
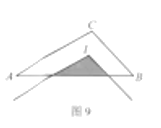
A.4.5 B.4 C.3 D.2
16.对于题目“一段抛物线![]() 与直线
与直线![]() 有唯一公共点.若
有唯一公共点.若![]() 为整数,确定所有
为整数,确定所有![]() 的值.”甲的结果是
的值.”甲的结果是![]() ,乙的结果是
,乙的结果是![]() 或4,则( )
或4,则( )
A.甲的结果正确
B.乙的结果正确
C.甲、乙的结果合在一起才正确
D.甲、乙的结果合在一起也不正确
二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有2个空,每空3分.把答案写在题中横线上)
17.计算:![]() .
.
18.若![]() ,
,![]() 互为相反数,则
互为相反数,则![]() .
.
19.如图![]() ,作
,作![]() 平分线的反向延长线
平分线的反向延长线![]() ,现要分别以
,现要分别以![]() ,
,![]() ,
,![]() 为内角作正多边形,且边长均为1,将作出的三个正多边形填充不同花纹后成为一个图案.
为内角作正多边形,且边长均为1,将作出的三个正多边形填充不同花纹后成为一个图案.

例如,若以![]() 为内角,可作出一个边长为1的正方形,此时
为内角,可作出一个边长为1的正方形,此时![]() ,而
,而![]() 是
是![]() (多边形外角和)的
(多边形外角和)的![]() ,这样就恰好可作出两个边长均为1的正八边形,填充花纹后得到一个符合要求的图案,如图
,这样就恰好可作出两个边长均为1的正八边形,填充花纹后得到一个符合要求的图案,如图![]() 所示.
所示.
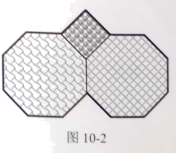
图![]() 中的图案外轮廓周长是 ;在所有符合要求的图案中选一个外轮廓周长最大的定为会标,则会标的外轮廓周长是 .
中的图案外轮廓周长是 ;在所有符合要求的图案中选一个外轮廓周长最大的定为会标,则会标的外轮廓周长是 .
三、解答题 (本大题共7小题,共66分.解答应写出文字说明、证明过程或演算步骤.)
20. 嘉淇准备完成题目:化简: ![]()
![]() 发现系数“
发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:
”猜成3,请你化简:![]() ;
;
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
21. 老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图![]() )和不完整的扇形图(图
)和不完整的扇形图(图![]() ),其中条形图被墨迹掩盖了一部分.
),其中条形图被墨迹掩盖了一部分.
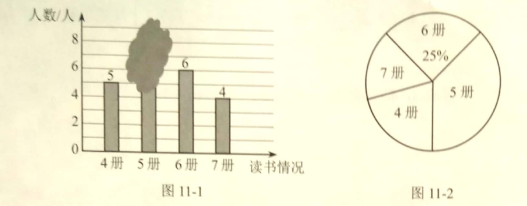
(1)求条形图中被掩盖的数,并写出册数的中位数;
(2)在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了 人.
22. 如图12,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着-5,-2,1,9,且任意相邻四个台阶上数的和都相等.
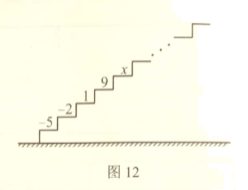
尝试(1)求前4个台阶上数的和是多少?
(2)求第5个台阶上的数![]() 是多少?
是多少?
应用 求从下到上前31个台阶上数的和.
发现 试用![]() (
(![]() 为正整数)的式子表示出数“1”所在的台阶数.
为正整数)的式子表示出数“1”所在的台阶数.
23. 如图13,![]() ,
,![]() 为
为![]() 中点,点
中点,点![]() 为射线
为射线![]() 上(不与点
上(不与点![]() 重合)的任意一点,连接
重合)的任意一点,连接![]() ,并使
,并使![]() 的延长线交射线
的延长线交射线![]() 于点
于点![]() ,设
,设![]() .
.
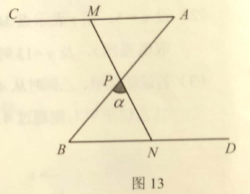
(1)求证:![]() ;
;
(2)当![]() 时,求
时,求![]() 的度数;
的度数;
(3)若![]() 的外心在该三角形的内部,直接写出
的外心在该三角形的内部,直接写出![]() 的取值范围.
的取值范围.
24. 如图14,直角坐标系![]() 中,一次函数
中,一次函数![]() 的图像
的图像![]() 分别与
分别与![]() ,
,![]() 轴交于
轴交于![]() ,
,![]() 两点,正比例函数的图像
两点,正比例函数的图像![]() 与
与![]() 交于点
交于点![]()
![]() .
.
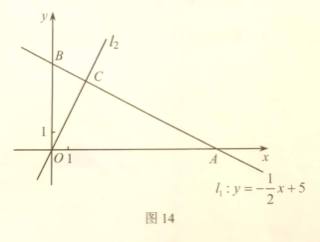
(1)求![]() 的值及
的值及![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)一次函数![]() 的图像为
的图像为![]() ,且
,且![]() ,
,![]() ,
,![]() 不能围成三角形,直接写出
不能围成三角形,直接写出![]() 的值.
的值.
25. 如图15,点![]() 在数轴上对应的数为26,以原点
在数轴上对应的数为26,以原点![]() 为圆心,
为圆心,![]() 为半径作优弧
为半径作优弧![]() ,使点
,使点![]() 在
在![]() 右下方,且
右下方,且![]() .在优弧
.在优弧![]() 上任取一点
上任取一点![]() ,且能过
,且能过![]() 作直线
作直线![]() 交数轴于点
交数轴于点![]() ,设
,设![]() 在数轴上对应的数为
在数轴上对应的数为![]() ,连接
,连接![]() .
.
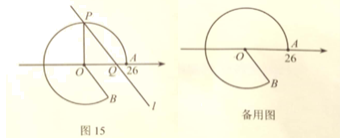
(1)若优弧![]() 上一段
上一段![]() 的长为
的长为![]() ,求
,求![]() 的度数及
的度数及![]() 的值;
的值;
(2)求![]() 的最小值,并指出此时直线与
的最小值,并指出此时直线与![]() 所在圆的位置关系;
所在圆的位置关系;
(3)若线段![]() 的长为
的长为![]() ,直接写出这时
,直接写出这时![]() 的值.
的值.
26.图16是轮滑场地的截面示意图,平台![]() 距
距![]() 轴(水平)18米,与
轴(水平)18米,与![]() 轴交于点
轴交于点![]() ,与滑道
,与滑道![]() 交于点
交于点![]() ,且
,且![]() 米.运动员(看成点)在
米.运动员(看成点)在![]() 方向获得速度
方向获得速度![]() 米/秒后,从
米/秒后,从![]() 处向右下飞向滑道,点
处向右下飞向滑道,点![]() 是下落路线的某位置.忽略空气阻力,实验表明:
是下落路线的某位置.忽略空气阻力,实验表明:![]() ,
,![]() 的竖直距离
的竖直距离![]() (米)与飞出时间(秒)的平方成正比,且
(米)与飞出时间(秒)的平方成正比,且![]() 时
时![]() ;
;![]() ,
,![]() 的水平距离是
的水平距离是![]() 米.
米.
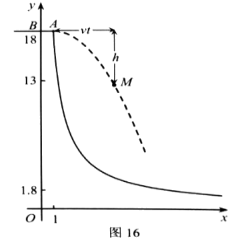
(1)求![]() ,并用表示
,并用表示![]() ;
;
(2)设![]() .用表示点
.用表示点![]() 的横坐标
的横坐标![]() 和纵坐标
和纵坐标![]() ,并求
,并求![]() 与
与![]() 的关系式(不写
的关系式(不写![]() 的取值范围),及
的取值范围),及![]() 时运动员与正下方滑道的竖直距离;
时运动员与正下方滑道的竖直距离;
(3)若运动员甲、乙同时从![]() 处飞出,速度分别是5米/秒、
处飞出,速度分别是5米/秒、![]() 米/秒.当甲距
米/秒.当甲距![]() 轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出的值及
轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出的值及![]() 的范围.
的范围.
参考答案
1-10、ABCCC DABDA 11-16、ABADB D
17、 2 18、 0 19、14 21
20、

21、


22、

23、

24、

25、

26、
