请选择
![]() 2018年巴中市高中阶段学校招生考试数学试卷
2018年巴中市高中阶段学校招生考试数学试卷
(全卷满分150分,120分钟完成)
第I卷选择题(共30分)
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项的番号涂卡.(本题共10个小题,每小题3分,共30分).
1. 下列各数:![]() ,0,
,0,![]() ,023,
,023,![]() ,
,![]() ,0.30003……,
,0.30003……,![]() 中无理数个数为( )
中无理数个数为( )
A. 2个 B. 3个 C.4个 D.5个
2. 某校师生在为青海玉树地震灾区举行的爱心捐款活动中总计捐款18.49万元,把18.49万用科学记数法表示并保留两个有效数字为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
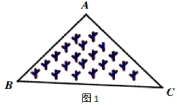
3. .如图1所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使京亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.![]() 的三条中线的交点 B.
的三条中线的交点 B.![]() 三边的中垂线的交点
三边的中垂线的交点
C.![]() 三条角平分线的交点 D.
三条角平分线的交点 D.![]() 三条高所在直线的交点
三条高所在直线的交点
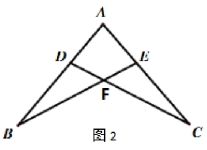
4. 如图2所示,![]() ,要说明
,要说明![]() ,需添加的条件不能是( )
,需添加的条件不能是( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
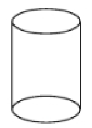
5. 如图3所示,以恒定的速度向此容器注水,容器内水的高度(![]() )与注水时间(
)与注水时间(![]() )之间的函数关系可用下列图像大致描述的是( )
)之间的函数关系可用下列图像大致描述的是( )
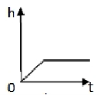
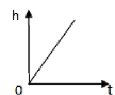
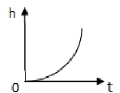
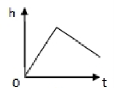
A. B. C. D.
6. 下列命题是真命题的是( )
A.若![]() ,则
,则![]() B.若
B.若![]() ,则
,则![]()
C. 若![]() ,则
,则![]() D.若
D.若![]() ,则
,则![]()
7. 函数![]() 的自变量
的自变量![]() 的取值范围是( )
的取值范围是( )
A.![]() 且
且![]() B.
B.![]() 且
且![]() C.
C.![]() D.全体实数
D.全体实数
8. 本学期的五次数学测试中,甲、乙两同学的平均成绩一样,方差分别为12、05,则下列说法正确的是( )
A.乙同学的成绩更稳定 B.甲同学的成绩更稳定
C. 甲、乙两位同学的成绩一样稳定 D.不能确定
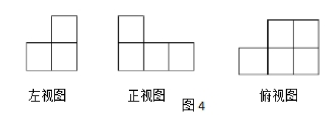
9. 图4是由大小一样的小正方块摆成的立体图形的三视图,它共用( )个小正方块摆成.
A. 5 B.8 C. 7 D.6
10. 巴广高速公路在5月10日正式通车,从巴中到广元全长约为![]() 一辆小汽车、一辆货车同时从巴中、广元两地相向开出,经过45分钟相遇,相遇时小汽车比货车多行
一辆小汽车、一辆货车同时从巴中、广元两地相向开出,经过45分钟相遇,相遇时小汽车比货车多行![]() ,设小汽车和货车的速度分别为
,设小汽车和货车的速度分别为![]() 、
、![]() ,则下列方程组正确的是( )
,则下列方程组正确的是( )
A.![]() B.
B. 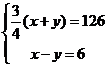 C.
C. 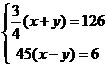 D.
D.
二、填空题:(每小题3分,满:30分,将正确答案直接填写在题中横线上)
11.![]() 的倒数的绝对值 .
的倒数的绝对值 .
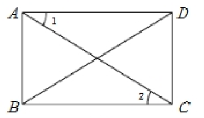
12. 如图5所示,已知□![]() ,下列条件:①
,下列条件:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,能说明□
中,能说明□![]() 是矩形的有 (填写番号).
是矩形的有 (填写番号).
13. 把多项式![]() 分解因式的结果是 .
分解因式的结果是 .
14. 点![]() ,点
,点![]() 是双曲线
是双曲线![]() 上的亮点,若
上的亮点,若![]() ,则
,则![]()
![]() (填“=”、“>”、“<”).
(填“=”、“>”、“<”).
15. 从下列图形中任选一个恰好是轴对称图开的概率为 .

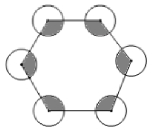
16. 如图6所示,以六边形的每个顶点为圆心,1为半径画圆,则图中阴影部分的面积为 .
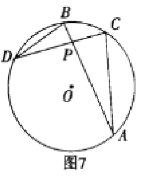
17. 如图7所示,![]() 的两弦
的两弦![]() 、
、![]() 交于点
交于点![]() ,连接
,连接![]() 、
、![]() ,得
,得![]() ,则
,则![]() .
.
18.![]() 与
与![]() 的半径分别是方程
的半径分别是方程![]() 的两根,如果两圆外切,那么圆心距
的两根,如果两圆外切,那么圆心距![]() 的值是 .
的值是 .
19. 直线![]() 与两坐标轴围成的三角形面积是 .
与两坐标轴围成的三角形面积是 .
20. 符号“![]() ”表示一种运算,它对一些数的运算结果如下:
”表示一种运算,它对一些数的运算结果如下:
(1)![]() ,
,![]() ,
,![]() ,
,![]() ,┄┄
,┄┄
(2)![]() ,
,![]() ,
,![]() ,
,![]() ┄┄.
┄┄.
利用以上规律计算: ![]() .
.
三、细心算一算(21题、22题各4分,23题、24题各5分,共18分)
21. 计算:![]()
22. 解分式方程:![]()
23. 解不等式组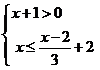 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
24. 若![]() ,求代数式
,求代数式![]() 的值.
的值.
四、推理认证(25题10分,26题10分,共20分)
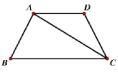
25. 已知如图8所示,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,连接
,连接![]() .
.
(1)求![]() 的值
的值
(2)若![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,连接
的中点,连接![]() ,求线段
,求线段![]() 的长.
的长.
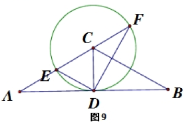
26. 已知如图9所示,![]() 中
中![]() ,
,![]() 是
是![]() 的角平分线,以
的角平分线,以![]() 为圆心,
为圆心,![]() 为半径画圆,交
为半径画圆,交![]() 所在直线于
所在直线于![]() 、
、![]() 两点,连接
两点,连接![]() 、
、![]() .
.
(1)求证:直线![]() 是
是![]() 的切线.
的切线.
(2)若![]() ,求
,求![]() 的长
的长
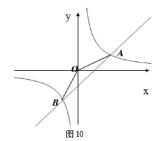
27. 一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,
,![]() 两点.
两点.
(1)求反比例函数的解析式
(2)求一次例函数的解析式
六、实践探索(28题10分,29题10分,共20分)
28. 今年5月,“全国科技列车巴中行”,在给我市带了医疗、农业、科普等方面的科技援助的同时,还在市直学校进行了一次“表少年心理干预”专题讲座,参加这次讲座的包括初中生150人,高中生200人教师50人,活动最后对参会人员进行了一次问卷调查(如下表)
“青少年心理干预”讲座效果统计表
效果 | 很好 | 较好 | 一般 | 不好 |
频数 | 240 |
|
| 8 |
频率 |
|
|
|
|
(1)活动结束后,记者随机抽取1人进行采访.恰好抽到初中生的机会是多少?
(2)请把上面的统计表补充完整.
(3)请根据统计表制作出频率分布扇形统计图.
29. “保护环境,人人有责”为了更好的治理巴河,巴中市污水处理厂决定购买![]() 、
、![]() 两型污水处理设备,共10台,其信息如下表:
两型污水处理设备,共10台,其信息如下表:
| 单价(万元/台) | 每台处理污水量(吨/月) |
| 12 | 240 |
| 10 | 200 |
(1)设购买4型设备![]() 台,所需资金共为
台,所需资金共为![]() 万元,每月处理污水总量为
万元,每月处理污水总量为![]() 吨,试写出
吨,试写出![]() 与
与![]() ,
,![]() 与
与![]() 的函数关系式.
的函数关系式.
(2)经预算,市污水处理厂购买设备的资金不超过106万元,月处理污水里不低于2040吨,请你列举出所有购买方案,并指出哪种方案最省钱,需要多少资金?
七、考考你有思维(10分)
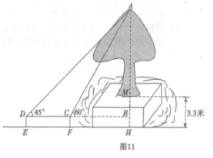
30.巴中市某中学数学兴趣小组在开展“保护环境,爱护树木”的活动中,利用课外时间,测量一棵古树的高,由于树的周围有水池,同学们在低于树基33米的一平坝内(如图11).则得树顶![]() 的仰角
的仰角![]() ,沿直线
,沿直线![]() 后退6米到点
后退6米到点![]() ,又测得树顶
,又测得树顶![]() 的仰角
的仰角![]() .若测角仪
.若测角仪![]() 高13米,求这棵树的高
高13米,求这棵树的高![]() .(结果保留两位小数,
.(结果保留两位小数,![]() )
)
八、拓展探索(12分)
31.如图12已知![]() 中,
中,![]() 以
以![]() 所在直线为
所在直线为![]() 轴,过
轴,过![]() 点的直线为
点的直线为![]() 轴建立平面直角坐标系.此时,
轴建立平面直角坐标系.此时,![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]()
(1)试求点![]() 的坐标
的坐标
(2)若抛物线![]() 过
过![]() 的三个顶点,求抛物线的解析式
的三个顶点,求抛物线的解析式
(3)点![]() 在抛物线上,过点
在抛物线上,过点![]() 的直线
的直线![]() 交(2)中的抛物线于点
交(2)中的抛物线于点![]() ,那么在
,那么在![]() 轴上点
轴上点![]() 的左侧是否存在点
的左侧是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?