请选择
![]() 荆门市2018年初中学业水平考试数学试题
荆门市2018年初中学业水平考试数学试题
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.![]() 的相反数的立方根是( )
的相反数的立方根是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.中国的陆地面积和领水面积共约![]() ,
,![]() 这个数用科学记数法可表示为( )
这个数用科学记数法可表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.在函数![]() 中,自变量
中,自变量![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.下列命题错误的是( )
A.若一个多边形的内角和与外角和相等,则这个多边形是四边形
B.矩形一定有外接圆
C.对角线相等的菱形是正方形
D.一组对边平行,另一组对边相等的四边形是平行四边形
5.已知直线![]() ,将一块含
,将一块含![]() 角的直角三角板(
角的直角三角板(![]() )按如图所示的位置摆放,若
)按如图所示的位置摆放,若![]() ,则
,则![]() 的度数为( )
的度数为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
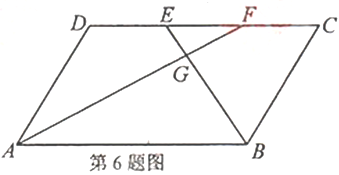
6.如图,四边形![]() 为平行四边形,
为平行四边形,![]() 、
、![]() 为
为![]() 边的两个三等分点,连接
边的两个三等分点,连接![]() 、
、![]() 交于点
交于点![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知关于![]() 的不等式
的不等式![]() 的最小整数解为
的最小整数解为![]() ,则实数
,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
8.甲、乙两名同学分别进行![]() 次射击训练,训练成绩(单位:环)如下表( )
次射击训练,训练成绩(单位:环)如下表( )
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六交 |
甲 | 9 | 8 | 6 | 7 | 8 | 10 |
乙 | 8 | 7 | 9 | 7 | 8 | 8 |
对他们的训练成绩作如下分析,其中说法正确的是
A.他们训练成绩的平均数相同 B.他们训练成绩的中位数不同
C.他们训练成绩的众数不同 D.他们训练成绩的方差不同
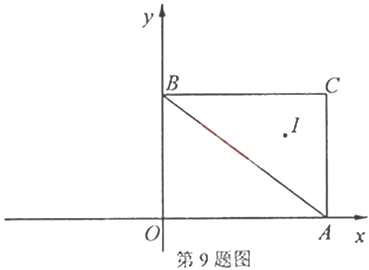
9.如图,在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的内心,将
的内心,将![]() 绕原点逆时针旋转
绕原点逆时针旋转![]() 后,
后,![]() 的对应点
的对应点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
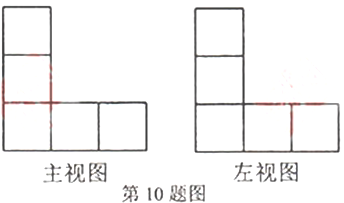
10.某几何体由若干个大小相同的小正方体搭成,其主视图与左视图如图所示,则搭成这个几何体的小正方体最少有( )
A.![]() 个 B.
个 B.![]() 个 C.
个 C.![]() 个 D.
个 D.![]() 个
个
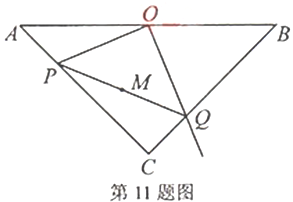
11.如图,等腰![]() 中,斜边
中,斜边![]() 的长为
的长为![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 边上的动点,
边上的动点,![]() 交
交![]() 于点
于点![]() ,
,![]() 为
为![]() 的中点,当点
的中点,当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,点
时,点![]() 所经过的路线长为( )
所经过的路线长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.二次函数![]() 的大致图象如图所示,顶点坐标为
的大致图象如图所示,顶点坐标为![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③若方程
;③若方程![]() 有两个根
有两个根![]() 和
和![]() ,且
,且![]() ,则
,则![]() ;④若方程
;④若方程![]() 有四个根,则这四个根的和为
有四个根,则这四个根的和为![]() .其中正确的结论有( )
.其中正确的结论有( )

A.![]() 个 B.
个 B.![]() 个 C.
个 C.![]() 个 D.
个 D.![]() 个
个
第Ⅱ卷(共90分)
二、填空题(每题3分,满分15分,将答案填在答题纸上)
13.计算:![]() .
.
14.已知![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的一个根,则
的一个根,则![]() 的值为 .
的值为 .
15.如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,则阴影部分的面积为 .
,则阴影部分的面积为 .

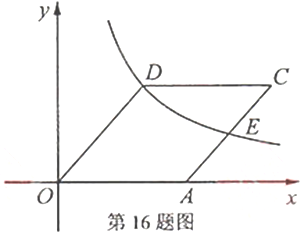
16.如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象经过菱形
的图象经过菱形![]() 的顶点
的顶点![]() 和边
和边![]() 的中点
的中点![]() ,若菱形
,若菱形![]() 的边长为
的边长为![]() ,则
,则![]() 的值为 .
的值为 .
17. 将数![]() 个
个![]() ,
,![]() 个
个![]() ,
,![]() 个
个![]() ,…,
,…,![]() 个
个![]() (
(![]() 为正整数)顺次排成一列:
为正整数)顺次排成一列:
![]() ,记
,记![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
,
![]() ,…,
,…,![]() ,则
,则![]() .
.
三、解答题 (本大题共7小题,共69分.解答应写出文字说明、证明过程或演算步骤.)
18. 先化简,再求值:![]() ,其中
,其中![]() .
.
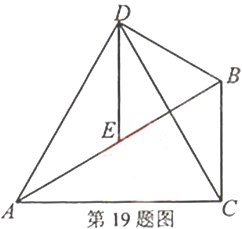
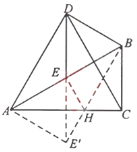
19. 如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边的中点,以
边的中点,以![]() 为边作等边
为边作等边![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,在
,在![]() 边上找一点
边上找一点![]() ,使得
,使得![]() 最小,并求出这个最小值.
最小,并求出这个最小值.
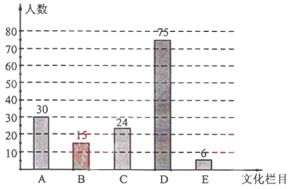
20. 文化是一个国家、一个民族的灵魂,近年来,央视推出《中国诗词大会》、《中国成语大会》、《朗读者》、《经曲咏流传》等一系列文化栏目.为了解学生对这些栏目的喜爱情况,某学校组织学生会成员随机抽取了部分学生进行调查,被调查的学生必须从《经曲咏流传》(记为A)、《中国诗词大会》(记为B)、《中国成语大会》(记为C)、《朗读者》(记为D)中选择自己最喜爱的一个栏目,也可以写出一个自己喜爱的其他文化栏目(记为E).根据调查结果绘制成如图所示的两幅不完整的统计图.
请根据图中信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)将条形统计图补充完整,并求出扇形统计图中“B”所在扇形圆心角的度数;
(3)若选择“E”的学生中有![]() 名女生,其余为男生,现从选择“E”的学生中随机选出两名学生参加座谈,请用列表法或画树状图的方法求出刚好选到同性别学生的概率.
名女生,其余为男生,现从选择“E”的学生中随机选出两名学生参加座谈,请用列表法或画树状图的方法求出刚好选到同性别学生的概率.

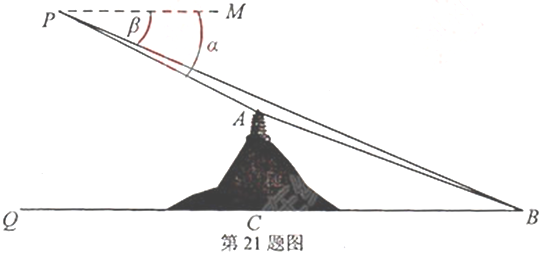
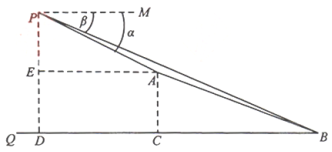
21. 数学实践活动小组借助载有测角仪的无人机测量象山岚光阁与文明湖湖心亭之间的距离.如图,无人机所在位置![]() 与岚光阁阁顶
与岚光阁阁顶![]() 、湖心亭
、湖心亭![]() 在同一铅垂面内,
在同一铅垂面内,![]() 与
与![]() 的垂直距离为
的垂直距离为![]() 米,
米,![]() 与
与![]() 的垂直距离为
的垂直距离为![]() 米,在
米,在![]() 处测得
处测得![]() 、
、![]() 两点的俯角分别为
两点的俯角分别为![]() 、
、![]() ,且
,且![]() ,
,![]() ,试求岚光阁与湖心亭之间的距离
,试求岚光阁与湖心亭之间的距离![]() .(计算结果若含有根号,请保留根号)
.(计算结果若含有根号,请保留根号)
22. 随着龙虾节的火热举办,某龙虾养殖大户为了发挥技术优势,一次性收购了![]() 小龙虾,计划养殖一段时间后再出售.已知每天养殖龙虾的成本相同,放养
小龙虾,计划养殖一段时间后再出售.已知每天养殖龙虾的成本相同,放养![]() 天的总成本为
天的总成本为![]() ,放养
,放养![]() 天的总成本为
天的总成本为![]() 元.设这批小龙虾放养
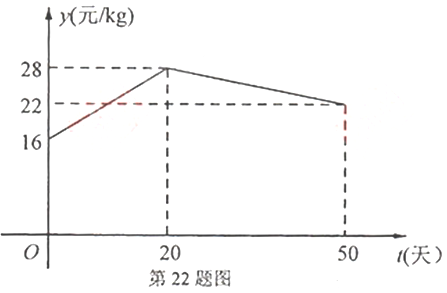
元.设这批小龙虾放养![]() 天后的质量为
天后的质量为![]() ,销售单价为
,销售单价为![]() 元/
元/![]() ,根据往年的行情预测,
,根据往年的行情预测,![]() 与
与![]() 的函数关系为
的函数关系为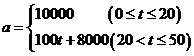 ,
,![]() 与
与![]() 的函数关系如图所示.
的函数关系如图所示.
(1)设每天的养殖成本为![]() 元,收购成本为
元,收购成本为![]() 元,求
元,求![]() 与
与![]() 的值;
的值;
(2)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)如果将这批小龙虾放养![]() 天后一次性出售所得利润为
天后一次性出售所得利润为![]() 元.问该龙虾养殖大户将这批小龙虾放养多少天后一次性出售所得利润最大?最大利润是多少?
元.问该龙虾养殖大户将这批小龙虾放养多少天后一次性出售所得利润最大?最大利润是多少?
(总成本=放养总费用+收购成本;利润=销售总额-总成本)
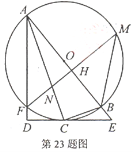
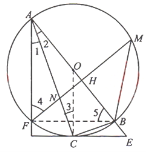
23.如图,![]() 为
为![]() 的直径,
的直径,![]() 为
为![]() 上一点,经过点
上一点,经过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() 交
交![]() 于
于![]() ,
,![]() 于
于![]() ,分别交
,分别交![]() 、
、![]() 于
于![]() 、
、![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:![]() 平方
平方![]() ;
;
(2)若![]() ,
,![]() ,①求
,①求![]() 的半径;②求
的半径;②求![]() 的长.
的长.
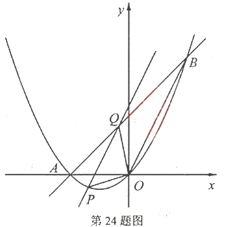
24.如图,抛物线![]() 与
与![]() 轴交于原点及点
轴交于原点及点![]() ,且经过点
,且经过点![]() ,对称轴为直线
,对称轴为直线![]() .
.
(1)求抛物线的解析式;
(2)设直线![]() 与抛物线两交点的横坐标分别为
与抛物线两交点的横坐标分别为![]() ,当
,当![]() 时,求
时,求![]() 的值;
的值;
(3)连接![]() ,点
,点![]() 为
为![]() 轴下方抛物线上一动点,过点
轴下方抛物线上一动点,过点![]() 作
作![]() 的平行线交直线
的平行线交直线![]() 于点
于点![]() ,当
,当![]() 时,求出点
时,求出点![]() 的坐标.
的坐标.
(坐标平面内两点![]() ,
,![]() 之间的距离
之间的距离![]() )
)
荆门市2018年初中学业水平考试数学试题试卷答案
一、选择题
1-5: CCBDA 6-10:CADAB 11、12:CB
二、填空题
13. ![]() 14.
14.![]() 15.
15.![]() 16.
16.![]()
17.![]() (
(![]() 亦可)
亦可)
三、解答题
18.解:原式
当![]() 时,
时,
原式![]()
![]()
19.(1)证明:在![]() 中,
中,![]() ,
,![]() 为
为![]() 边的中点,
边的中点,
∴![]() ,
,![]() .
.
∵![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
∴![]()
(2)解:如图,作点![]() 关于直线
关于直线![]() 点
点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
则点![]() 即为符合条件的点.
即为符合条件的点.
由作图可知:
![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 的最小值为
的最小值为![]() .
.
20.解:(1)![]() (人),∴共调查了
(人),∴共调查了![]() 名学生.
名学生.
(2)![]() :
:![]() (人),
(人),![]() :
:![]() (人)
(人)
补全条形图如图所示.
扇形统计图中“![]() ”所在扇形圆心角的度数为
”所在扇形圆心角的度数为![]() .
.
(2)记选择“![]() ”的同学中的
”的同学中的![]() 名女生分别为
名女生分别为![]() ,
,![]() ,
,![]() 名男生分别为
名男生分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
或画树形图:
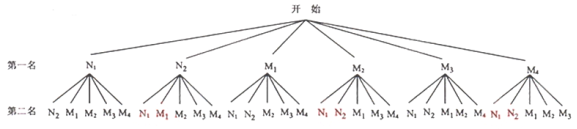
∵共有![]() 种等可能的结果,其中,恰好是同性别学生(记为事件
种等可能的结果,其中,恰好是同性别学生(记为事件![]() )的有
)的有![]() 种情况,
种情况,
∴![]() .
.
21.解:过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .由题意得:
.由题意得:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
∵![]() ,∴四边形
,∴四边形![]() 为矩形,
为矩形,
∴![]() ,
,![]() ,∴
,∴![]() ,
,
在![]() 中,
中, ,
,
∴![]()
在![]() 中,
中,![]() (米)
(米)
答:岚光阁与湖心亭之间的距离![]() 为
为![]() 米.
米.
22.(1)依题意得![]() ,解得
,解得![]()
(2)当![]() 时,设
时,设![]() ,由图象得:
,由图象得: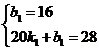 ,解得
,解得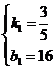
∴![]()
当![]() 时,设
时,设![]() ,由图象得:
,由图象得: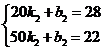 ,解得
,解得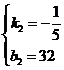
∴![]()
综上,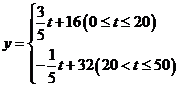
(3)![]()
当![]() 时,
时,![]()
∵![]() ,∴当
,∴当![]() 时,
时,![]()
当![]() 时,
时,![]()
![]()
∵![]() ,抛物线开口向下,∴当
,抛物线开口向下,∴当![]() ,
,![]() .
.
∵![]()
∴当![]() 时,
时,![]() 取得最大值,该最大值为
取得最大值,该最大值为![]() 元.
元.
23.(1)证明:连接![]() ,
,
∵直线![]() 与
与![]() 相切于点
相切于点![]() ,
,
∴![]() ,
,
又∵![]() ,∴
,∴![]() .
.
∴![]()
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() 平方
平方![]() .
.
(2)解:①∵![]() ,∴
,∴![]()
又∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]()
设![]() 的半径为
的半径为![]() ,
,
则![]() ,解得
,解得![]()
②连接![]() ,
,
∵![]() 为
为![]() 的直径,∴
的直径,∴![]() ,∴
,∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() 为
为![]() 的直径,∴
的直径,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴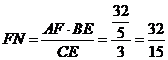 .
.
24.(1)由题意得: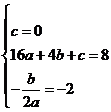 ,解得
,解得![]() ,
,
![]() ,
,
(2)由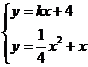 得
得![]() ,
,
![]() ,
,![]()
∵![]() ,∴
,∴![]() ,
,
![]()
![]() ,解得
,解得![]()
(3)设直线![]() 的方程为
的方程为![]() ,且经过点
,且经过点![]() ,∴
,∴![]() ,解得
,解得![]() ,
,![]()
设![]() ,∵
,∵![]() ,设直线
,设直线![]() 的解析式为
的解析式为![]() ,
,
∴![]() ,
,![]()
设直线![]() 的解析式为
的解析式为![]() ,
,![]() ,
,![]()
∴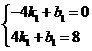 ,解得
,解得![]() ,
,![]()
联立![]() ,解得
,解得![]() , ∴
, ∴![]()
∵![]() ,
,![]() ,∴
,∴![]()
而![]() ,∴
,∴![]() ,
,![]() ,
,
解得![]() 或
或![]()