请选择
一、选择题:本大题共10小题,每题3分,共30分.
1.第24届冬季奥林匹克运动会,将于2022年02月04日~2022年02月20日在中华人民共和国北京市和张家口市联合举行.在会徽的图案设计中,设计者常常利用对称性进行设计,下列四个图案是历届会徽图案上的一部份图形,其中不是轴对称图形的是( )
A.
B.
C.
D.
2.下列各式运算中结果是a6是( )
A.a3+a3
B.(a3)3
C.a12÷a2
D.a3•a3
3.下列各式由左边到右边的变形中,是因式分解的是( )
A.x3﹣xy2=x(x﹣y)2
B.(x+2)(x﹣2)=x2﹣4
C.﹣2x2﹣2xy=﹣2x(x+y)
D.x2+2x+1=x(x+2)+1
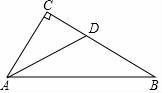
4.如图,在△ABC中,∠C=90°,AD是∠BAC的角平分线,若CD=2,AB=8,则△ABD的面积是( )
A.6
B.8
C.10
D.12
5.如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.
步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3:连接AD,交BC延长线于点H.
下列叙述正确的是( )
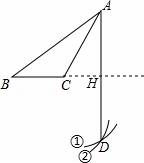
BH垂直平分线段AD
B.AC平分∠BAD
S△ABC=BC•AH
D.AB=AD
6.如图,△ABC中,D、E两点分别在AC、BC上,则AB=AC,CD=DE.若∠A=40°,∠ABD:∠DBC=3:4,则∠BDE=( )

A.25°
B.30°
C.35°
D.40°
7.多项式x2﹣mxy+9y2能用完全平方因式分解,则m的值是( )
A.3
B.6
C.±3
D.±6
8.若a,b,c是三角形的三边,则代数式(a﹣b)2﹣c2的值是( )
A.正数
B.负数
C.等于零
D.不能确定
9.如图,在三角形纸片ABC中,∠C=90°,∠B=30°,点D(不与B,C重合)是BC上任意一点,将此三角形纸片按下列方式折叠,若EF的长度为a,则△DEF的周长为( )
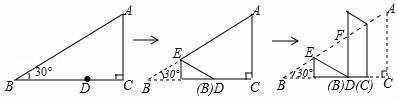
A.2a
B.2.5a
C.3a
D.4a
10.如图,四边形ABCD中,AB=AD,点B关于AC的对称点B'恰好落在CD上,若∠BAD=α,则∠ACB的度数为( )
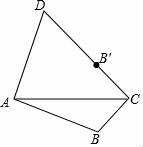
A.45°
B.α﹣45°
C.2分之1α
D.90°﹣2分之1α
二、填空题:本大题共7小题,每题4分,共28分.把你的答案填入答题纸中相应的位置上.
11.(4分)点P(2,﹣3)关于x轴的对称点坐标为( ).
12.(4分)等腰三角形的一个内角为100°,这个等腰三角形底角的度数为( ).
13.(4分)已知xm=4,xn=3,则xm+n的值为( ).
14.(4分)若(2x﹣1)0无意义,则代数式(4x2﹣1)2008的值为( ).
15.(4分)如图,在△ABC中,AB=AC,D,E,F分别在BC,AC,AB上的点,且BF=CD,BD=CE,∠FDE=α,则∠A的度数是( )度.(用含α的代数式表示)
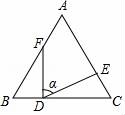
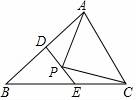
16.(4分)如图,在△ABC中,AC=6,BC=8,AB的垂直平分线DE交AB边于点D,交BC边于点E,在线段DE上有一动点P,连接AP、PC,则△APC的周长最小值为( ).
17.(4分)已知(a﹣2018)2+(2019﹣a)2=5,则(a﹣2018)(2019﹣a)=( ).
三、解答题:本大题共9小题,共62分.
18.(12分)计算下列各题:
(1)3x•6x2y
(2)(a+2b)(a﹣2b)
(3)a•a5﹣(a2)3﹣(﹣2a3)2
(4)[x(x2y2﹣xy)﹣y(x2﹣x3y)]÷3x2y.
19.(9分)把下列各式分解因式:
(1)a2b+ab2
(2)ab2﹣4ab+4a
(3)x2(a﹣b)+y2(b﹣a)
20.如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C,AF与DE相交于点O,请判断△OEF的形状,并说明理由.

21.先化简,再求值:(x+3)(x﹣3)+(2x﹣1)2﹣4x(x﹣1),其中x=![]() .
.
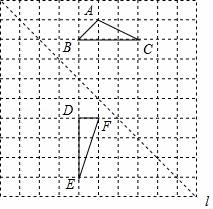
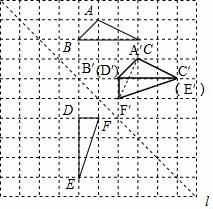
22.(4分)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
(1)将△ABC向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形.
(2)画出△DEF关于直线l对称的三角形.
(3)填空:∠C+∠E=( ).
23.已知:线段AB.
(1)尺规作图:作线段AB的垂直平分线l,与线段AB交于点D;(保留作图痕迹,不写作法)
(2)在(1)的基础上,点C为l上一个动点(点C不与点D重合),连接CB,过点A作AE⊥BC,垂足为点E.
①当垂足E在线段BC上时,直接写出∠ABC度数的取值范围.
②请你画出一个垂足E在线段BC延长线上时的图形,并求证∠BAE=∠BCD.
![]()
24.(6分)对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到(a+b)2=a2+2ab+b2,请解答下列问题:
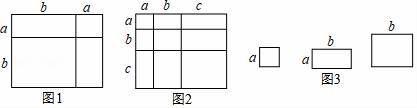
(1)写出图2中所表示的数学等式( ).
(2)根据整式乘法的运算法则,通过计算验证上述等式.
(3)利用(1)中得到的结论,解决下面的问题:
若a+b+c=10,ab+ac+bc=35,则a2+b2+c2=( ).
(4)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形z张边长分别为a、b的长方形纸片拼出一个面积为(5a+7b)(9a+4b)长方形,则x+y+z=( ).
25.(7分)定义:如图1,在△ABC和△ADE中,AB=AC=AD=AE,当∠BAC+∠DAE=180°时,我们称△ABC与△DAE互为“顶补等腰三角形”,△ABC的边BC上的高线AM叫做△ADE的“顶心距”,点A叫做“旋补中心”.
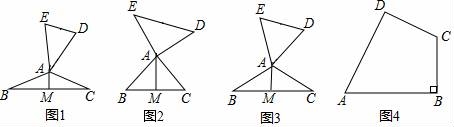
(1)特例感知:在图2,图3中,△ABC与△DAE互为“顶补等腰三角形”,AM是“顶心距”.
①如图2,当∠BAC=90°时,AM与DE之间的数量关系为AM=( )DE;
②如图3,当∠BAC=120°,ED=6时,AM的长为( ).
(2)猜想论证:
在图1中,当∠BAC为任意角时,猜想AM与DE之间的数量关系,并给予证明.
(3)拓展应用
如图4,在四边形ABCD中,AD=AB,CD=BC,∠B=90°,∠A=60°,CD=![]() ,在四边ABCD的内部找到点P,使得△PAD与△PBC互为“顶补等腰三角形”.并回答下列问题.
,在四边ABCD的内部找到点P,使得△PAD与△PBC互为“顶补等腰三角形”.并回答下列问题.
①请在图中标出点P的位置,并描述出该点的位置为( );
②直接写出△PBC的“顶心距”的长为( ).
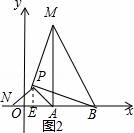
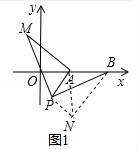
26.(9分)(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b且填空:当点A位于( )时,线段AC的长取得最大值,且最大值为( )(用含a、b的式子表示).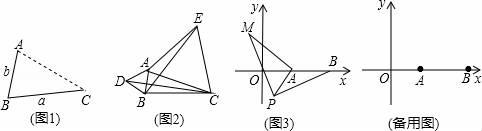
(2)应用:点A为线段BC外一动点,且BC=4,AB=2,如图2所示,分别以AB,AC为边,作等边三解形ABD和等边三角形ACE,连接CD,BE.①请找出图中与BE相等的线段,并说明理由; ②直接写出线段BE长的最大值.
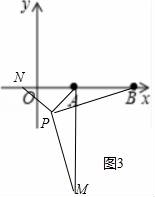
(3)拓展:如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.
参考答案
一、选择题:本大题共10小题,每题3分,共30分.
1.D.2.D.3.C.4.B.5.A.
6.B.7.D.8.B.9.C.10.D.
二、填空题:本大题共7小题,每题4分,共28分.把你的答案填入答题纸中相应的位置上.
11.(2,3).12.40°.13.答案:12.
14.0 15.180°﹣2α 16.14.17.﹣2.
三、解答题:本大题共9小题,共62分.
18.解:(1)原式=18x3y;
(2)原式=a2﹣4b2;
(3)原式=a6﹣a6﹣4a6=﹣4a6;
(4)原式=(x3y2﹣x2y﹣x2y+x3y2)÷3x2y
=(2x3y2﹣2x2y)÷3x2y
=![]() xy﹣
xy﹣![]() .
.
19.解:(1)a2b+ab2=ab(a+b);
(2)ab2﹣4ab+4a=a(b2﹣4b+4)=a(b﹣2)2;
(3)x2(a﹣b)+y2(b﹣a)=(a﹣b)(x2﹣y2)=(a﹣b)(x+y)(x﹣y).
20.解:△OEF的形状为等腰三角形.
理由如下:∵BE=CF,
∴BE+EF=CF+EF,即BF=CE.
在△ABF与△DCE中,
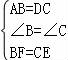 .
.
∴△ABF≌△DCE(SAS).
∴∠AFB=∠DEC.
∴OE=OF,即△OEF的形状为等腰三角形.
21.解:原式=x2﹣9+4x2﹣4x+1﹣4x2+4x=x2﹣8,
当x=根号7时,原式=7﹣8=﹣1.
22.解:(1)△A′B′C′即为所求;
(2)△D′E′F′即为所求;
(3)45°.
23.解:(1)直线l即为所求作的直线.(见图1)

(2)①45°≤∠ABC<90°.
理由如下:连接AC,
当∠ACB≤90°时垂足E在线段BC上,
∵CD垂直平分AB,
∴CA=CB,
∴∠CAB=∠CBA,
∵2∠CBA+∠ACB=180°,
∴2∠CBA≥90°
∴∠CBA≥45°
∵∠CBA是锐角,
∴45°≤∠CBA<90°
②在图2中,
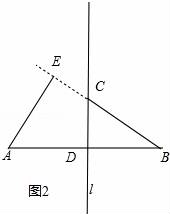
证明:∵线段AB的垂直平分线为l,
∴CD⊥AB,
∵AE⊥BE,
∴∠AEB=∠BDC=90°,
∴∠BAE+∠B=∠BCD+∠B=90°,
∴∠BAE=∠BCD.
24.(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
(2)30;
(4)156.
25.解:(1)2分之1
②3
(2)猜想:结论AM=2分之1DE.
理由如下:如图,过点A作AN⊥ED于N

∵AE=AD,AN⊥ED
∴∠DAN=2分之1∠DAE,ND=2分之1DE
同理可得:∠CAM=2分之1∠CAB,
∵∠DAE+∠CAB=180°,
∴∠DAN+∠CAM=90°,
∵∠CAM+∠C=90°
∴∠DAN=∠C,
∵AM⊥BC
∴∠AMC=∠AND=90°
在△AND与△AMC中,
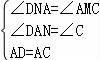
∴△AND≌△AMC(AAS),
∴ND=AM
∴AM=2分之1DE
(3)①线段BC的垂直平分线交AC于点P,
②2分之根号3
解:(1)CB的延长线上,a+b;
(2)①CD=BE,
理由:∵△ABD与△ACE是等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠CAD=∠EAB,
在△CAD与△EAB中,
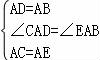 ,
,
∴△CAD≌△EAB,
∴CD=BE;
②∵线段BE长的最大值=线段CD的最大值,
由(1)知,当线段CD的长取得最大值时,点D在CB的延长线上,
∴最大值为BD+BC=AB+BC=6;
(3)连接BM,∵将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,
则△APN是等腰直角三角形,
∴PN=PA=2,BN=AM,
∵A的坐标为(2,0),点B的坐标为(5,0),
∴OA=2,OB=5,
∴AB=3,
∴线段AM长的最大值=线段BN长的最大值,
∴当N在线段BA的延长线时,线段BN取得最大值,
最大值=AB+AN,
∵AN=根号2AP=2根号2,
∴最大值为2 根号2+3;
如图2,过P作PE⊥x轴于E,
∵△APN是等腰直角三角形,
∴PE=AE=根号2,
∴OE=BO﹣AB﹣AE=5﹣3﹣根号2=2﹣根号2,
∴P(2﹣根号2,根号2).
如图3中,根据对称性可知当点P在第四象限时,P(2﹣根号2,﹣根号2)时,也满足条件.
综上所述,满足条件的点P坐标(2﹣根号2,根号2)或(2﹣根号2,﹣根号2),AM的最大值为2![]() +3.
+3.