请选择
返回
经过某一条线段的中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线,接下来分享垂直平分线的性质和判定方法。

垂直平分线的性质
(1)垂直平分线垂直且平分其所在线段。
(2)垂直平分线上任意一点,到线段两端点的距离相等。
(3)三角形三条边的垂直平分线相交于一点,该点叫外心,并且这一点到三个顶点的距离相等。
(4)垂直平分线的判定:必须同时满足①直线过线段中点;②直线⊥线段。
垂直平分线判定方法
(1)利用定义:经过某一条线段的中点,并且垂直于这条线段的直线是线段的垂直平分线
(2)到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.(即线段垂直平分线可以看成到线段两端点距离相等的点的集合)。
垂直平分线的逆定理
逆定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
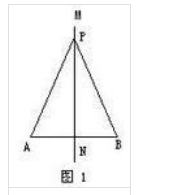
如图1,已知N是AB中点,MN是AB的垂直平分线,平面上一点P满足PA=PB,证明:P在MN上。
解:∵MN是AB的垂直平分线,∴AN=BN
∵PA=PB ,PN=PN,∴△PAN≌△PBN,∴∠PNA=∠PNB
∵∠PNA+∠PNB=180°,∴∠PNA=∠PNB=90°
由于过平面上一点,有且仅有一条直线与已知垂线垂直,故P在MN上。
该逆定理得证。