数学中充要条件什么意思

充分必要条件就是条件与结论可以相互推导，根据条件可以推出结论，根据结论也可以推出条件。这样的条件就是充要条件。

充要条件

充分必要条件也即充要条件，意思是说，如果能从命题p推出命题q，而且也能从命题q推出命题p ，则称p是q的充分必要条件，且q也是p的充分必要条件。

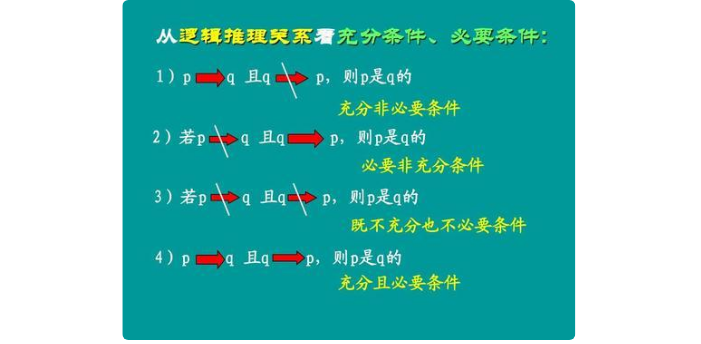
举例

1.A=“三角形等边”；B=“三角形等角”。

2.A=“某人触犯了法律”；B=“应当依照刑法对他处以刑罚”。

3.A=“付了足够的钱”；B=“能买到商店里的东西”。

例1中A是B的充分必要条件；

例2中A是B的必要不充分条件：（A触犯法律包含各种法，有刑法有民法；B已经确定是刑法。B属于A所以A是B的必要不充分条件）

例3中A是B的必要不充分条件；（ A付够了钱 可以买的是车 房子等；但是B能买到超市里的东西一定是要付够钱）

充分条件

如果A能推出B，那么A就是B的充分条件。其中A为B的子集，即属于A的一定属于B，而属于B的不一定属于A，具体的说若存在元素属于B的不属于A，则A为B的真子集；若属于B的也属于A，则A与B相等。

必要条件

必要条件是数学中的一种关系形式。如果没有A，则必然没有B；如果有A而未必有B，则A就是B的必要条件，记作B→A，读作“B含于A”。数学上简单来说就是如果由结果B能推导出条件A，我们就说A是B的必要条件。