请选择
循环小数怎么表示:循环节的表示方法。找到小数部分的循环小数,如果它是一个数字循环,就在这个数字的上面点一个点;如果2个数字循环,就在这两个数字上面分别点一个点;如果出现2个以上数字的,就在第一个数字和最后一个数字的上面点一个点。

循环小数怎么表示
一、循环节表示
循环节的表示方法。找到小数部分的循环小数,如果它是一个数字循环,就在这个数字的上面点一个点;如果2个数字循环,就在这两个数字上面分别点一个点;如果出现2个以上数字的,就在第一个数字和最后一个数字的上面点一个点。
循环小数的缩写法是将第一个循环节以后的数字全部略去,而在第一个循环节首末两位上方各添一个小点。
例如:35.232323…缩写为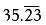
(它读作“三十五点二三,二三循环”)
二、分数表示
把循环小数的小数部分化成分数的规则:
1、纯循环小数小数部分化成分数:将一个循环节的数字组成的数作为分子,分母的各位都是9,9的个数与循环节的位数相同,最后能约分的再约分。
2、混循环小数小数部分化成分数:分子是第二个循环节以前的小数部分的数字组成的数与不循环部分的数字所组成的数之差,分母的头几位数字是9,9的个数与一个循环节的位数相同,末几位是0,0的个数与不循环部分的位数相同。

循环小数一定是无限小数对吗
这句话是正确的循环小数一定是无限小数。因为,循环小数的定义:一个数的小数部分从某一位起,一个或几个数字依次重复出现的无限小数叫循环小数。循环小数首先是在无限小数的基础上讲的,所以循环小数一定是无限小数。
循环小数的注意事项
1、无理数的定义是无限不循环小数,由此可以判定无限不循环小数是无理数(因为定义也是判定)。
2、混循环:将混循环小数改写成分数,分子是不循环部分与第一个循环节连成的数字组成的数,减去不循环部分数字组成的数之差;分母的头几位数字是9,末几位数字是0,9的个数跟循环节的数位相同,0的个数跟不循环部分的数位相同。