请选择
返回
小编为大家整理了中线有关的数学知识,大家跟随小编学习一下吧。

中线含义
中线是三角形中从某边的中点连向对角的顶点的线段。中线也是线段,一个三角形有3条中线。三角形的三条中线总是相交于同一点,这个点称为三角形的重心,重心分中线为2:1(顶点到重心:重心到对边中点)。
等腰三角形腰上中线
等腰三角形的两腰上的中线长相等。
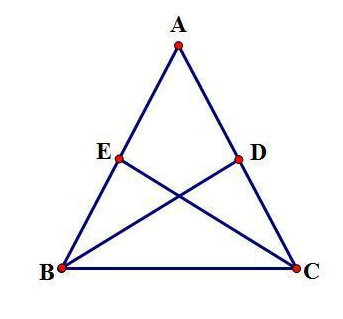
设在等腰三角形ABC中,AB=AC,BD、CE分别是腰AC、AB的中线,求证:BD=CE。
证明:
∵BD、CE分别是AC、AB的中线
∴AD=1/2AC,AE=1/2AB,
∵AB=AC,
∴AD=AE,
又∵∠A=∠A,
∴△ABD≌△ACE(SAS)
∴BD=CE。
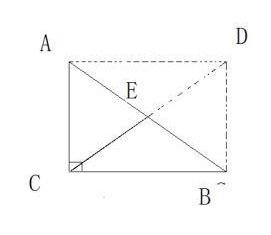
直角三角形斜边中线
延长CE至点D,使CE=DE,连接AD,BD
∵CE是AB上的中线
∴AE=EB
∵CE=DE
∴四边形ABCD是平行四边形
∵∠ACB=90°
∴平行四边形ABCD是矩形
∴AB=CD,AE=BE,CE=DE
∴AE=BE=CE=DE
∴CE=1/2CD=1/2AB
以上是小编整理的特殊三角形中的中线的知识,希望给大家带来帮助。